Monte, Guidobaldo del , In duos Archimedis aequeponderantium libros paraphrasis, 1588

Bibliographic information

Author: Monte, Guidobaldo del
Title: In duos Archimedis aequeponderantium libros paraphrasis
Date: 1588

Permanent URL

Document ID: MPIWG:N7454WBP
Permanent URL: http://echo.mpiwg-berlin.mpg.de/MPIWG:N7454WBP

Copyright information

Copyright: Max Planck Institute for the History of Science (unless stated otherwise)
License: CC-BY-SA (unless stated otherwise)
1
GVIDIVBALDI
E MARCHIONIBVS
MONTIS
IN DVOS ARCHIMEDIS
ÆQVEPONDERANTIVM
LIBROS
PARAPHRASIS
Scholijs illuſtrata.
1[Figure 1]
PISAVRI
Apud Hieronymum Concordiam;
M D LXXXVIII.
Superiorum Conceſſu.
1
[Empty page]
1
SERENISSIMO
FRANC.^{CO} MARIAE
II. VRBINI DVCI.
GVIDVSVBALDVS
E' MARCHIONIBVS MONTIS S.
Iam decemnium elapſum eſt, DVX Sere­
niſſime, ex quo de rebus machanicis volu­
men, veras (ni fallor) mirabilium mechani­
corum effectuum cauſas manifeſtans, in lu­
cem dedi; vbi non nulla antiquiora, præci­
pua〈que〉 illuſtrium græcorum authorum pla­
cita ad ſuſceptum negotium pertinentia,
tanquam rectę rationi magis conſentanea amplexatus ſum.
quibus ſanè, tanquam ſolidiſſimis innixa fundamentis, theo­
remata multa, ac varia conſtruxi. quippe quæ, licet non inua­
lidis quo〈que〉 demonſtrationum præſidijs à me ipſo munita
fuerint; pleriſquè tamen, qui non admodum fortaſſe in huiuſ­
modi rerum cauſis inueſtigandis verſati exiſtunt, noua pror­
ſus (vt accepi) ac ferme inaudita, nec ſatis (vt opinor) apud eos
firma, at〈que〉 ideo illis non omnino ſatisfeciſſe, viſa ſunt. Quo­
circa cogitanti mihi, qua ratione fieri poſſet, vt opus illud à
me editum, quàm plurimorum ſibi gratiam in dies magis con
ciliaret, in mentem venit, non aliunde id mihi oportuniùs con
tingere potuiſſe, quàm ſi priſcos ipſos, & grauiſſimos alioqui
authores de hac re elegantiſſimè diſſerentes illis offerrem. ra­
tus, vt ſolidiſſimâ eorum doctrinâ, quæ à me propoſita, & ex­
1plicata fuere theoremata, firmiora redderentur. ſimulquè alio
rum ambiguitati, ne dicam imbecillitam ſuccurreretur. vel ſal
tem ipſi grauiſſima eorum authoritate non nullorum captiua­
rent intellectum, in obſequium meliùs, rectiùſquè ſentientium,
at〈que〉 intelligentium. Nihil enim tam, aut a conſuetudine, aut
ab opinione remotum eſſe ſolet, quod ſola authoritate proba­
ri non poſſit. Verùm ne huiuſmodi negotium in recenſendis
multorum ad propoſitam veritatem confirmandam teſtimo­
nijs latiùs, quàm par eſſet, protraheretur; mihi conſtitui, ex mul
tis vnicum tantùm, eumquè reliquorum omnium hac in par
te facilè principem deligere: qui, & meam cauſam tueretur: &
illis, ſi fieri poſſet, ſatisfaceret: vt〈que〉 grave; coràm illis ipſe ſe offerens,
tanquam meo quo〈que〉 nomine miſſus intelligeretur; quibuſ­
dam meis notis non inſignitum certè, ſed aſſociatum eundem
prodire volui. Eſt autem grauiſſimus hic author Syracuſius ille
Archimedes de mechanicis elementis conſultiſſimè diſſerens.
cuius nimirum dignitati, at〈que〉 authoritati, vt omnes probè à
me conſultum intelligerent; decreui, vt 〈que〉madmodum inter
alios illius ordinis viros primatum obtinet, ita nulli alij, quàm
amplitudini tuę DVX Sereniſſime, hac noſtra ętate, doctrina,
rerumquè omnium cognitione ſingulari, citra controuerſiam
Principi ſupremo, ſuum in primis hoc tempore præſtaret obſe
quium. quod incredibili ſanè animi mei iucunditate conti­
giſſe fateor; non ſolùm, vt rurſum aliquam ſingularis meæ er­
ga amplitudinem tuam obſeruantiæ, ac venerationis, tot, tan­
tiſquè nominibus iam pridem debitę teſtificationem ederem;
verùm etiam, vt munuſculo illi meo tanto Principi audentiùs
fortaſſe antea oblato, ne prorſus prę ſua tenuitate deſpiceretur,
opem ferret. quanquam ne〈que〉 id quidem, pro eximia animi
tam excelſi magnitudine, ſuſpicandum fuit. Per hunc ergo tam
celebrem authorem ad te Princeps optime, ac pręſtantiſſime
lætabundus accedo. Is enim mihi, 〈que〉madmodum & ego ipſi,
ad te aditum patefeciſſe videtur; & ſicut eundem tibi longe gra­
tiſſimum futurum confido; ita me tui amantiſſimum, & obſer
uantiſſimum, vt eâdem, qua conſueuiſti, benignitate proſe­
quaris, oro ſuplex, & obſecro. Aueto dulce præſidium, ac ętatis
noſtræ ſplendidum decus; & eſto perpetuò fęlix.
1
GVIDIVBALDI
E MARCHIONIBVS
MONTIS.
PRAEFATIO:
Mechanica facultas non ſolùm ab imperitis,
verùm etiam ab eruditis admirabilis ſem­
per habita fuit; eorum enim, quę in admi­
rationem homines trahunt, duo eſſe gene­
ra Ariſtoteles in principio ſuarum quęſtionum
Meehanicarum aſſeruit; quorum ſanè alte
rum ad ea pertinet, quæ natura quidem,
proximis tamen ipſorum cauſis latentibus in lucem prodeunt;
alterum verò ſpectat ad ea, quę pręter naturam, & arte fiunt;
quibus natura ſuperari videtur (quamquam & ipſa plurimùm
momenti ad ſe ipſam euincendam tune quo〈que〉 afferat) &
quod naturę uiribus in lucem prodire nequit, id arte fieri con
tingat, ob idquè maiorem adhuc admirationem excitat, quòd
ars naturę ęmula, quaſi aduerſus naturam ipugnans, cam ſupe­
ret, & tanquan vim ipſi in ferre videatur; cuius ſanè operationis
cauſa quo〈que〉 cognita admirationem parit; cùm exigua admo
dum ad tanti operis productionem appareat. admirabile eſt ſa­
nè ipſius artis magiſterium, cùm adeò potens ſit, vt effectus na­
turę repugnantes producere tentet. quippè quibus, niſi ita ſen
ſibus ſubijciàntur; vt tangi propemodum, & conſpici poſſint,
vix fides adhibeatur; idquè non ſine admiratione adhuc cogni
tum, ac perſuaſum nobis eſſe poſſit. huiuſmodi autem mira­
bilium operum opifex eſt ipſa mechanica diſciplina, tam na­
turę ęmula, quàm oppugnatrix valida. Hęc enim grauia pro
prio fermè nutu ſurſum attolli, magnaquè pondera ab exigua
1admodum virtute moueri, aliaquè id genus huiuſmodi ſpe­
ctanda proponit. vt tum imperitis ex ipſorummet effectuum
intuitu, tum eruditis in cauſarum varia contemplatione ad­
mirationem pariat. veluti ſi ea ſpectemus, quę neruis, vel ali­
quo mouétur inſtrumento; vel quę ſpiritibus concinnuntur, &
fiunt; de quibus Heron, & alij pertractarunt; vel deni〈que〉 alijs
modis. quamquam nos in ijs, quæ dicenda ſunt, de ea mecha­
nicæ facultatis parte, quæ ad pondera, diſtantiaſ〈que〉 inter ipſa exi­
ſtentes pertinet, quorum ſtatus ad ęquilibrium reduci poteſt, ver
ba faciemus. quæ quidem pars totius mechanicę facultatis prin­
ceps exiſtit. ea enim eſt, in qua artem ſuperare naturam aper­
tiùs conſpicitur: quod quidem, qua ratione contingat, hinc pla
num euadet.
Ars quippe ex Ariſtotele phiſicorum ſecundo, & ex proæ­
mio quæſtionum mechanicarum triplici modo in ſuis opifi­
cijs ſeſe habere videtur. Nam vel immitatur naturam; vel ea
perficit, quæ natura perficere non poteſt; vel deni〈que〉 ea, quæ
pręter naturam fiunt, operatur; in quibus tamen omnibus o­
perandi rationibus, ſi diligenter eas conſideremus, artem ſem­
per immitari naturam perſpiciemus. Primùm quidem multas
artes naturam immitari aperte videmus, vt ſculpturam, & hu­
iuſmodi alias. Quando autem ars ea perficit, quæ ſola natu­
ra perficere non poteſt, vt in arte medica euenire ſolet; naturam
ipſam pariter emulatur, & naturæ aſſociata, velut inſtrumen­
tum eius, naturalem effectum perficere dicitur: tuncquè eodem
modo operatur, ac ſi natura rem ipſam abſ〈que〉 artis ope perfice
repoſſet, quod planè artis præſtantiam manifeſtat: quippè
cùm niſi ars ipſi naturæ manum porrigat, natura ipſa proprios
effectus perficere ex ſeſe minimè poſſit. At verò ſi ars naturam
immitando ipſam ſuperauerit; vt ea, quæ ab arte fiunt, præter
naturam eueniant, longè adhuc præſtantiùs artis ingenium
apparebit. ſiquidem immitando naturam (paradoxum id for
tè videbitur, cùm tamen veriſſimum ſit) præter naturæ ordi­
nem operari dicatur. Ars. enim mirabili artificio naturam ipsa na
tura ſuperat; ita nimirum res diſponendo, vt ipſa efficeret na
tura, ſi eiuſmodi ſibi producendos ſtatueret effectus. quod qui
dem ſubiecto exemplo magis perſpicuum fiet.
1
Sint enim duo pondera

AB in aliquo vecte, A ma
ius, B minus; quorum ſi­
mul ita in vecte diſpoſito­
rum ſit centrum grauitatis
C. ſit autem ſub vecte in­
ter CA fulcimentum in D.
& quoniam pondera AB penes C grauitatis centrum inclinan
tur? tunc C deorſum naturaliter mouebitur; ac per conſe〈qué〉s
pondus quo〈que〉 B deorſum tendet. Sed ſi B deorſum mouetur,
A certè ſurſum eleuabitur. quippe quod, quamuis, vt graue eſt,
at〈que〉 ſolutum abſ〈que〉 connexione ponderis B deorſum tende
ret; attamen vt adnexum ponderi B, intercedente vecte AB,
ſurſum mouebitur: & (vt ita dicam) pondus A contra pro­
priam naturam naturaliter aſcendet. Vndè perſpicuum eſt, hos
motus effectus eſſe naturales. Quid igitur efficit ars ipſa? nil
fanè aliud, quàm quòd resita diſponit, & accomodat; vt ſimi­
les effectus inde prodeant at〈que〉 ſi naturales omnino exiſtant,
quare opus erit, ut Ars naturam immitetur, ſiquidem effectus
naturales prouenire debent. propterea vectem, fulcimentum­
què eodem modo diſponit; & loco ponderis B aliquam con­
ſtituit potentiam, quæ pręmendo parem vim habeat grauita­
ti ipſius B; at〈que〉 tunc ipſa potentia mouens, quę minoreſt gra
uitate ponderis A, ipſum A grauius nihilominus attollet.
quod quamuis propriæ ipſius naturæ repugnet, naturaliter ta­
men ab ipſa potentia in B exiſtente ſursum feretur: res enim ita di
ſpoſitæ talem habent naturam, vt A quidem ſurſum, B vero
deorſum moueri debeant. quę ſanè ex noſtro Mechanicorum
libro, & ex ijs, quæ in hoc pertractantur; compertiſſimè red­
dentur, & quod diximus devecte, de alijs quo〈que〉 in ſtrumen­
tis mechanicis intelligendum eſt. quorum quidem apparatus
ſunt artis opera, effectus autem ipſius penè naturæ: cùm eius
momenta, inclinationesquè ſequantur, veluti præcipuas eiuſ­
modi operum effectrices cauſas: quippè quæ ſunt omnino ad­
mirabiles, ac pręſtantiſſime; 〈que〉madmodum ex ipſarum con
templatione patere poteſt. cuius rei argumentum illud indicaſſe ſat
eſto, nimirum eas à ſummis uiris, Ariſtotele, & Archimede fuiſſe
1pertractatas. Ariſtoteles. enim in principio Quęſtionum mechanica­
rum multa, ea〈qué〉 pręcipua ad cauſas rei mechanicæ dignoſcendas
aperuit; 〈qué〉 ſecutus Archimedes in his libris mechanica prin­
cipia explicatiùs patefecit, eaquè planiora reddidit. Nec propte
rea Ariſtoteles diminutus extitit: etenim eorum, quę ab ipſo pro
poſita, & explicata fuere, problematum cauſas egregiè patefe­
cit. ſed quoniam Archimedi ſcopus fuit mechanicę diſciplinę
rudimenta explanare; propterea ad magis particularia enucleam
da deſcendere voluit. Ariſtoteles. enim (gratia exempli) quęrens cur
vecte magna mouemus pondera? cauſam eſſe ait longitudinem
vectis maiorem ad partem potentiæ: & rectè quidem; cùm ex
principio ab ipſo conſtituto manifeſtum ſit, ea, quę ſunt in
longiori à centro diſtantia, maiorem quo〈que〉 habere virtuté. Ar­
chimedes verò vlteriùs adhuc progredi voluit, hoc admiſſo, nem
pè quod eſt in longiori diſtantia maiorem uim habere, quàm
id, quod eſt in breuiori, inquirere etiam voluit, quanta ſit vis
eius, quod eſt in longiori diſtantia ad id, quod eſt in breuiori;
ita vt inter hęc nota reddatur qualis, & quę ſit eorum propor­
tio determinata. at〈que〉 ideo fundamentum illud mechanicum
pręſtantiſſimum manifeſtauit; videlicet ita ſeſe habere pon­
dus ad pondus, vt diſtantia ad inſtantiam, vnde pondera ſu­
ſpenduntur, ſeſe permutatim habet. quo ignoto, res mechani­
cę nullo modo pertractari poſſe videntur. quandoquidem
huic tota mechanica facultas tanquam vnico, pręcipuo〈que〉
fundamento innititur. Quare Archimedes Ariſtotelem ſequi vide
tur; quod non ſolùm patet exijs, quæ dicta ſunt; verùm etiam
ſi Archimedis poſtulata conſiderauerimus, quibus conſtituendis,
ea, quæ de principijs mechanicis Ariſtoteles patefecit, Archi­
medé ſupponere comperiemus. vt deinceps ſuo loco perſpicuum
fiet. In ratione pręterea, ac modo conſiderandi mechanica, maxi­
ma ambo affinitate coniuncti in cedere vidétur. Ariſtoteles. enim
res mechanicas tum Mathematica, tú naturalia ſapere, ac reſpi
cere aſſeruit: quod quidem & Archimedes optimè nouit: nam quę
Mathematicè ſunt conſideranda, geometricè demonſtrauit,
vt ſunt diſtantiæ, proportiones, & alia huiuſmodi: quæ verò
ſunt naturalia, naturaliter quo〈que〉 conſiderauit; vt ea, quæ ad gra
uitatis centrum ſpectant, & quæ ſurſum, & quę deorſum moue
1ri debent; & cętera huiuſmodi. Ex quibus patet maximum eſſe
inter tantos viros in his pertractandis conſenſum. Ambiget
fortaſſe quiſpiam, nunquid hęc principia rectè ab illis fuerint
pertractata? ſed ſtatim omnis ceſſat dubitandi occaſio, ſi tan
torum virorum pręſtantia ad memoriam reuocetur; quibus,
citra controuerſiam in diſciplinis ab ipſis traditis, omnes eru­
diti palmam deferunt. vt 〈que〉madmodum abſ〈que〉 Ariſtotele duce,
at〈que〉 doctore, nemo ad rectè philoſophandum, ita ne〈que〉 etiam
ad Mathematicam, pręcipue〈que〉 Mechanicam diſciplinam
abſ〈que〉 Archimede ſeſe quiſpiam diſponere poſſit: quorum ſanè
apud peritiores authoritas meritò ob id ſuprema extat; quòd
ab ipſis res eo meliori, pręſtantiori〈que〉; modo pertractatę fuerunt,
quo ipſarum rerum natura, at〈que〉 doctrinę ratio poſtulabat. &
qui ſcientiarum cupidi ſunt, illos ſequi, eorum què ſcripta ſępè
ſępius attentè perlegere debent. Pręterea philoſophię, ac Ma­
thematicę profeſſores in hoc conueniunt; quòd cùm aliqua ad
philoſophiam ſpectantia tractant; mirum in modum Ariſto­
telem laudibus extollunt. qui verò Mathematicas pertractare
ſtudét, ſtatim ad Archimedis laudes pariter ſe conferunt. tametſi
circa ea, quę nó ſunt Archimedis verſentur; vt quam plurimi fece
re, quod quidem optimo factum eſt conſilio. etenim ſi ea, quæ
mathematica ope indigent, laudare volunt, ad Archimedem
confugiendum eſt; vt ſi inuentionem, ſubtiliſſimum Archi­
medis inuentum afferant, quo modum adinuenit cognoſcen­
dę quantitatis argenti, quod erat in corona Regis aurea, vt Vi­
truuius teſtatur; & alia huiuſmodi; ſi admirabilia, ſtatim affe­
rant Archimedis ſphęram in globo vitreo elaboratam, in qua
omnes cęleſtis ſphæræ motus relucebant; ita ut natura potiùs
Archimedem immitata, quàm Archimedes naturam illuſiſſe
videatur; nauim præterea graui pondere oneratam è mari in
littus ab Archimede eductam; aliaquè id genus plurima. De­
ni〈que〉 ſi res Mathematicas ciuitatibus eſſe vtiles oſtendere vo­
lunt, ea, quæ ab Archimede contra Marcellum in defenſio­
ne patriæ facta fuere, in medium afferant, quo tempore bellica
opera adeo mirabilia effecit, vt ſolus Archimedes contra bel
licoſiſſimos Romanos pugnare ſufficiens videretur. quæ qui­
dem omnia Mechanica diſciplina confecta ſunt. Quid igitur
1Mechanica admirabilius, & vtilius? è qua tot, tantaquè ad
humani generis vtilitatem conferentia prodeunt? eximia cer­
tè, & præclara admodum hæc Archimedis geſta fuere; quæ ta­
men, ſi ad alia quamplurima, quæ de ipſo dici, ac afferri poſ
ſunt, conferantur; exigua ſanè mihi videntur. Nam quæ ha­
ctenus commemorata ſunt, (quamquam fortaſſe non omnia)
multa tamen, huiuſmodiquè ſimilia alij quo〈que〉 effecerunt,
& adhuc extant fortaſſe viri eo ingenij acumine pręditi, qui
talia aggredi non vererentur: ſed nonnulla egregia extant ipſius
Archimedis opera, quorum ſimilia, nec antea, nec poſt ipsum
facta fuere, ne〈que〉 in futurum facienda fore à nemine ſint ex­
pectanda. omnium enim admirabiliſſima, præſtantiſſima­
què ſunt eius ſcripta, in quibus, & ingenij acumen, inuentio­
nes ſubtiliſſimæ, perfectaquè doctrina planè conſpicitur. adeo
enim his omnibus Archimedis ſcripta aliorum ſcripta mathe
maticorum excellunt, ſuperantquè; vt quæ aliorum, facilè
quidem inter ſeſe comparari, cum ijs verò, quę ab Archimede
nobis relicta fuerunt; nullo modo poſſint. ut apertiſsimè
(alijs interim omiſsis) conſpicuum redditur ex ijs, quæ de
ſphęra & cylindro, & ex ijs, quę de æ〈que〉ponderantibus ſcri­
pta reliquit: quippè quę ob eorum pręſtantiam, ac dignitatem
meritò literis aureis eſſent imprimenda. liber enim de ſphęra,
& cylindro inter Archimedis ſcripta excellens adeò habitus fuit;
vt ad eius sepulcrum appoſita fuerit ſphęra, & cylindrus: quibus a
Cicerone conſpectis; ſtatim illud Archimedis sepulcrum eſſe in
tellexit: de cuius inuentione ob uiri excellentiam maximè glo­
riatur: Deindè qua ratione ipſum à temerario vanę orationis
proferendæ auſu, (dum ſic loquitur, da mihi vbi ſiſtam, ter­
ramquè mouebo) vindicare poſſemus; niſi hęc, quæ de æ〈que〉­
ponderantibus extant, ſcripta reliquiſſet? ex his enim habita
notitia proportionis ponderum, & diſtantiarum, ſit manife­
ſtum non eſſe à ratione, nequè à natura prorſus alienum, poſſe
terram moueri, ſi daretur conſiſtendi locus. quod etiam ex
noſtro volumine Mechanico annis ab hinc aliquot elapſis e­
dito varijs quoquè inſtrumentis parere poteſt. quandoquidem
multis modis, datum pondus à data potentia moueri, ibi oſtem
ſumeſt. vbi demonſtrationes à nobis conſtitutę ijs, quæ apud
1Archimedem preſenti opere habentur, totam eorum vim fer­
ri volunt acceptam. Etne quidpiam, quod ſtudioſis mecha­
nicæ facultatis prodeſſe poſſit, prętermitteretur, ad horum
Archimedis librorum interprætationem aliquid operis con­
tuliſſe placuit; ſatisquè nobis feciſſe videbimur; ſi ſaltem ſtu­
dioſi nos Archimedis veſtigia ſecutos fuiſſe cognouerint.
Et quamuis opus hoc fuerit ab Eutocio Aſcalonita nonnullis
commentarijs illuſtratum, quia tamen propter Archimedis
ſcriptorum obſcuritaté multa adhuc remanét abſtruſa, nec pror
ſus omnibus peruia; pręſertim gręcarum literarum experti­
bus; cùm liber hic in latinum verſus multis in locis obſcurus,
alijsquè pleris〈que〉 quodammodo mancus meritò ſuſpicetur;
ita vt adhuc in tenebris iacere videatur; gręcusquè præterea
codex impreſſus, 〈que〉m ſecuti ſumus, multis in locis aliqua
correctione egere videatur; idcirco ab huiuſmodi munere
pręſtando deſiſtere noluimus: quin ſimul hos libros in latinum
ſermonem verteremus; commentarijsquè illuſtratos redde­
remus. Cùm præſertim hinc tutus ad mechanicam diſciplinam
pateat aditus. Quare vt mens huius pręclariſſimi Mathema
tici magis, at〈que〉 magis, quàm fieri poſsit, pro virili noſtra
perſpicua reddatur; & huius ſcientiæ cupidi in adipiſcendis
pulcherrimis hiſce theorematibus minùs laborent; à commu
ni genere interprętandi aliquantulum in præſentia diſcedere
nobis viſum eſt oportunum. Nam qui res mathematicas in­
terprætati ſunt, ſuos commentarios ſeorſum à demonſtratio­
nibus collocauere: nos verò, quę noſtra ſunt, verbis ipſius
Archimedis inſeruimus, & hoc tantùm in ipſis demonſtra­
tionibus, non in propoſitionibus, & huiuſmodi alijs, hac
planè habita diſtinctione, vt quæ ſunt Archimedis (his, vel
his literarum notis) cognoſcantur, ipſiusquè tantùm Ar­
chimedis eſſe intelligantur. Quę verò alterius ſunt cha­
racteris, utquę huius exiſtent formæ, noſtra eſſe ſemper
ſint exiſtimanda. & quoad fieri potuit, verba omnia, quę
nobis declaratione aliqua, nec non correctione indigere viſa
ſunt (ijs tamen omiſſis, quę parui, imò nullius ſunt momenti,
vt eſt literarum immutatio, & huiuſmodi alia) dilucidè expli­
care, at〈que〉 emendare ſtuduimus. quibus etiam hanc adhibui
1mus diligentiam, quod quamuis ea, quæ noſtra, ſunt, verbis
ſint Archimedis inſerta; ſiquis tamen verba tantùm Archi­
medis legere maluerit, rectè id aſſequi poterit; ſiquidem ne
verbum quidem Archimedis omiſimus: quinnimo ea ita di­
ſpoſuimus, vt ſuum prorſus retineant ſenſum, poſſintquè con
tinuatè legi; ac ſi nihil inter ipſa inſertum fuerit. quod qui­
dem ſtudioſis non inutile fore iudicauimus; qui abſ〈que〉 no­
ſtris additionibus Archimedem tantùm habebunt; cum noſtris
verò additionibus Archimedis demonſtrationes continua­
tas, & explicatas habebunt. Huberionis autem doctrinæ gra
tia permulta adiunximus ſcholia, in quibus paſſim ordinem,
Authoriſquè artificium patefecimus; nec non multa lemma
ta ad Archimedis demonſtrationes neceſſaria demonſtraui­
mus; aliaquè nonnulla ad explicationem, ſubiectamquè ma
teriam valde vtilia adiecimus. Vt etiam Archimedis dicta
magis eluceſcant, antequam ad explicationem verborum
ipſius accedamus, nonnulla prius declarare oportunum no­
bis viſum eſt ad ea, quæ in his libris Archimedis ſupponit
tanquam cognita. Deinde conſiderandus proponitur ſcopus,
at〈que〉 intentio Archimedis; diuiſio item librorum; huiuſ­
modiquè alia, quæ ſummam afferent facilitatem ad intel
ligendam: mentem Archimedis.
in princip.
〈que〉ſt. Me­
chan.
Claudianus
declaratio
huius para
phraſis.
2[Figure 2]
Cùm itaquè ſupponat, nos exquiſitam habere notitiam
centri grauitatis; illius definitionem afferre libuit: pro cuius
tamen faciliori notitia illud quo〈que〉 in primis admonen­
 dum duximus; nimirum quatuor reperiri centra. Centrum ui­
delicet vniuerſi, centrum magnitudinis, centrum figuræ, &
centrum grauitatis, quod quidem grauitatis centrum rectè
definitur à Pappo Alexandrino in octauo libro mathemati­
carum collectio num hoc pacto.
DEFINITIO CENTRI GRAVITATIS
Centrum grauitatis vniuſcuiuſ〈que〉 corporis eſt punctum
quoddam intra poſitum, à quo ſi graue appenſum mente
conçipiatur, dum fertur, quieſcit & ſerua eam, quam in
principio habebat poſitionem, neque in ipſa latione
1uertitur.
EIVSDEM ALIA DEFINITIO.
Centrum grauitatis vniuſcuiuſ〈que〉 ſolidæ figuræ eſt punctum
illud intra poſitum, circa quod vndi〈que〉 partes ęqualium mo
mentorum conſiſtunt. ſi. enim per tale centrum ducatur planum fi
guram quomodo cun〈que〉 ſecans, ſemper in partes æ〈que〉ponde
rantes ipſam diuidet.
Hanc poſtremam definitionem, ſeu potiùs deſcriptionem
tradidit Federicus Commandinus in libro de centro grauita­
tis ſolidorum. ex quipus ſanè definitionibus eluceſcit natura,

at〈que〉 facultas centri grauitatis.
vt ſi punctum A fuerit centrum
grauitatis corporis BC, tunc
ex Pappi ſententia, ſi BC ſuſpem
datur ex A, magnitudo BC
eadem, qua reperitur, diſpo­
ſitione locata manebit; ne〈que〉
partes ullas ipſius corporis, vt quę ſunt ad

BC, circumuerti, ne〈que〉 omnino ſuum
mutare ſitum depræhendetur. ſi verò vt
Commandino placuit, A fuerit centrum
grauitatis magnitudinis BCD, eadem­
què per punctum A vtcun〈que〉 ſecundùm
rectitudinem diuidatur, veluti per EAF.
tunc pars EBF ipſi ECDF æ〈que〉ponde­
rabit, quamuis EBF, & ED ſint magni
tudines inæquales. ſæpenumero enim e­
uenire ſolet, vt in diuiſione figuræ per eius centrum graui­
tatis ipſa aliquando in partes diuidatur æquales, ali­
quando in partes inæquales: vt ſuo loco
ſemper tamen in partes diuiditur hinc inde æ〈que〉pon­
derantes; non tamen ſeorſum conſtitutas, ab inuicen
què ſeiunctas, & veluti ad æquilibrium examinatas; vt pu­
ta ſi EBF decem pondo ponderet; ED quo〈que〉 totidem
pependiſſe oporteat. res quippe non ſic ſe habet, ſed cas eſſe
in eo ſitu æ〈que〉ponderantes, in quo reperiuntur; vt neutra
1alteri pręponderet. ex quibus colligi poteſt, ſi graue quidpiam
in centro mundi collo catum fuerit, oportere centrum graui
tatis illius in centro mundi conſtitutum eſſe: ſiquidem vt
graue illud tunc quieſcat, partes vndi〈que〉 ipſum ambientes ę­
qualium momentorum exiſtere, at〈que〉 manere oporteat.
Quare dum aſſeritur, graue quod cum〈que〉 naturali propen­
ſione ſedem in mundi centro appetere, nil aliud ſignifica­
tur, quàm quòd eiuſmodi graue proprium centrum grauitatis
cum centro vniuerſi coaptare expetit, vt optimè quieſcere va­
leat. Ex quo ſequitur motum deorſum alicuius grauis fieri
per rectam lineam, quæ centrum grauitatis ipſius grauis, cen
trumquè mundi connectit. quandoquidem grauia deorſum
rectà feruntur. Vnde manifeſtum eſt, Grauia ſecundum gra
uitatis centrum deorſum tendere. quod nos in noſtro Mecha
nicorum libro ſuppoſuimus.
in fine pri­
mi huius.
3[Figure 3] 4[Figure 4]
Ex ijs omnibus, quæ hactenus de centro grauitatis dicta
ſunt, perſpicuum eſt, vnumquod〈que〉 graue in eius centro
grauitatis propriè grauitare, veluti nomen ipſum centri gra­
uitatis idipſum manifeſtè præſeferre videtur. ita vt tota vis,
grauitaſquè ponderis in ipſo grauitatis centro coaceruata, col
lectaquè eſſe, ac tanquam in ipſum vndiquè fluere videatur.
Nam ob grauitatem pondus in centrum vniuerſi naturaliter per
uenire cupit; centrum verò graui tatis (exdictis) eſt id, quod
propriè in centrum mundi tendit. in centro igitur grauitatis
pondus propriè grauitat. Præterea quando aliquod pondus
ab aliqua potentia in centro grauitatis ſuſtinetur; tunc pon­
dus ſtatim manet, totaquè ipſius ponderis grauitas ſenſu per­
cipitur. quod etiam contingit, ſi ſuſteneatur pondus in ali­
quo puncto, à quo per centrum grauitatis ducta recta linea
in centrum mundi tendat. hoc nam〈que〉 modo idem eſt, ac
ſi pondus in eius centro grauitatis propriè ſuſtineretur. Quod
quidem non contingit, ſi ſuſtineatur pondus in alio pun­
cto. ne〈que〉 enim pondus manet, quin potiùs antequam ipſius
grauitas percipi poſſit, vertitur vti〈que〉 pondus, donec ſimi
liter à ſuſpenſionis puncto ad centrum grauitatis ducta re­
cta linea in vniuerſi centrum recto tramite feratur.
quæ quidem ex prima noſtrorum Mechanicorum
1poſitione ſunt manifeſta, quando autem hæc linea eſt hori­
zonti erecta, tunc idem prorſus eſt (vt mox diximus) perinde
ac ſi pondus in centro grauitatis ad vnguem ſuſtineretur.
Quocirca ſi pònderis grauitas minimè percipi poteſt, niſi in
centro grauitatis ipſius, pondus certè in ipſo propriè grauitat.
Centrum figuræ apud Mathematicos eſt punctum, à quo
ſemidiametri exeunt; vel per quod tranſeunt diametri, vt circu
li centrum, & ellipſis, necnon oppoſitarum ſectionum.
Centrum verò magnitudinis eſt id, quod medium figuræ
obtinet; vel quod ęqualiter ab exteriori ſuperficie diſtat. vt
ſphærę centrum.
Centrum deni〈que〉 mundi eſt punctum in medio vniuerſi
ſitum, omniumquè rerum infimum.
Cæterùm ad meliorem horum notitiam obſeruandum eſt,
hęc centra aliquando ſimul omnia inter ſe conuenire, aliquam
do nonnulla; aliquando autem minimè. ſimul verò omnia
conueniunt. vt centrum vniuerſi, centrum magnitudinis ter
ræ (ſphęræ ſcilicet ex aqua, terraquè compoſitę, quam nos bre
uitatis ſtudio terram tantùm nuncupabimus) centrum figu­
rę terrę; ac centrum grauitatis terrę. Cùm enim terra ſit ſphæ­
rica (vt omnes fatentur.) eius medium erit centrum figurę, à
quo ſemidiametri exeunt. idipſum què erit centrum magnitu
dinis, ſiquidem ipſius figurę medium obtinet. Pręterea idem
punctum eſt centrum grauitatis terrę. & quoniam terra in me
dio mundi quieſcit, erit hoc centrum grauitatis in centro vniuerſi
collocatum. & hoc duntaxat modo centra omnia in vnum con
uenire poſſunt. quamquam verò ſphęra, quę continet terram &
aquą, compoſita eſt ex corporibus diuerſę ſpeciei, differentiſquè
grauitatis, nimirum ex terra, & aqua; non tamen efficitur, quin
medium ipſius cum centro grauitatis conſpiret in vnum. Nam ex
Ariſto telis ſententia terra circa mundi centrum vndi〈que〉 conſi
ſtit; & Archimedes affirmat, etiam humidum manens ſphęri­
cum, cuius centrum eſt centrum vniuerſi. ſi ita 〈que〉 terra, & aqua ma
nent, quieſcuntquè circa centrum vniuerſi, ergo centrum mundi ipſo­
rum ſimul centrum grauitatis exiſtit. at〈que〉 adeo quatuor prędicta
centra in vnum ſimul conueniunt punctum. Quod autem tria ſi
mul centra in vnum coeant, ſatis conſpicuum eſſe poterit cuiquè
1ſphæram aliquam, putà ligneam, vel alterius (ſimilaris tamen)
naturæ intuenti; ſiquidem eius medium erit centrum magni­
tudinis, & centrum figuræ; idemquè punctum erit ipſius cen­
trum grauitatis; circa quod vndi〈que〉 partes æ〈que〉ponderant.
& quoniam hæc ſphæra non eſt in centro mundi; propterea
tria tantùm centra ſimul conuenient. ſi verò ſphęra non ſimi­
laris, ſed diſſimilaris fuerit, veluti altera ipſius meditate plum­
bea, altera verò medietate lignea exiſtente, tunc eius medium
erit quippe centrum magnitudinis, & figurę, grauitatis verò
centrum nequaquam. Nam partes vndi〈que〉 circa medium æ­
〈que〉ponderare non poſſent; ſed grauitatis centrum ad grauio­
rem partem, nimirum plumbeam declinabit. & hoc modo
duo tantùm centra inter ſe conuenient. vt etiam (modo ta­
men diuerſo) accidit ellipſi; cuius centrum eſt centrum figu­
rę, ſiquidem per ipſum tranſeunt diametri; idemquè punctum
eſt ipſius centrum grauitatis. quod cùm non ſit propriè me­
dium figuræ, non erit quo〈que〉 centrum magnitudinis. medium
enim figuræ propriè circulo, ac ſphæræ tantùm competit.
Quare duo centra hoc quo〈que〉 modo ſimul tantùm conue­
nient. In figura paraboles recta linea terminatę centrum gra
uitatis intra figuram reperitur, quippè quod ne〈que〉 centrum
figuræ, ne〈que〉 centrum magnitudinis eſſe poteſt. etenim in
hac figura non poteſt dari medium, vnde ne〈que〉 centrum ma
gnitudinis dabitur, & quoniam in parabole diametri ſunt in
terſe ęquidiſtantes, vt ex primo libro conicorum Apollonij
Pergei conſtat; ne〈que〉 etiam centrum figuræ dabitur. ſic igi­
tur centra nullo modo conuenient.
lib. de cælo
lib. de iis
quę uehun
tur in aqua
16 Federi­
ci comm. de
centro gra
uitatis ſoli
dorum.
4. Fed. com
man. de cen
tro graui­
tatis ſolido
rum.
in ſecundo
libro huius
Nouiſſe quo〈que〉 oportet centrum grauitatis communius
eſſe, in pluribuſquè reperiri, quàm centra magnitudinis, & fi­
guræ: centrum verò figuræ communius eſſe centro magnitu­
dinis. Nam quodlibet corpus, & quęlibet figura neceſſe eſt, vt habeat
centrum grauitatis intrinſecùs, vel extrinſecùs. intrinſecùs vt
centrum grauitatis alicuius corporis regularis, quod eſt in medio
figuræ, vel alicuius figuræ vt A; cuius centrum grauitatis ſit
in ambitu figuræ, vt in puncto B; extrinſecùs verò vt figura
C, cuius centrum grauitatis extrinſecus ſit, vt in D; quod
eſt intelligendum, ſi graue C in centrum mundi tenderet,
1tunc centrum D cum centro mundi con­

ueniret; figuraquè C quieſceret circa cen
trum vniuerſi, veluti ſe habet circa centrum
D. partes enim figuræ talem poſſunt ha­
bere ſitum, vt inter ſe ę〈que〉ponderare poſ­
ſint. vt ex ſubiectis figuris perſpicuum eſt.
& ad huc clariùs, ſi intelligatur figura, vt
E circulo tum exteriori, tum interiori ter
minata, cuius centrum grauitatis extra fi­
guram erit in F. quod quidem cum cir­
culorum centro conueniet. circa quod
(exiſtente centro F in centro mundi)
partes vndi〈que〉 ę〈que〉ponderabunt: cùm
omnes ęqualiter à centro grauitatis diſtent.
præterea in hac figura E centrum graui­
tatis (quamuis ſit extra figuram) cum cen­
tro figuræ, centroquè magnitudinis ipſius
figuræ conuenire, fortaſſe non erit incon­
ueniens aſſerere. At verò figuræ AC nul
lo pacto figuræ, magnitudinisquè centrum
habebunt. & quamuis dictum ſit centrum
grauitatis corporum regularium eſſe me­
dium ipſorum, non tamen propterea dicendum eſt, idem eſſe
centrum magnitudinis, at〈que〉 figuræ, niſi impropriè; medium
enim his impropriè attribuitur, ſicuti etiam centrum figuræ;
cùm lineæ ex ipſo prodeuntes non ſint ipſorum corporum
(quatenus regularia ſunt) ſemidiametri. quare centrum gra­
uitatis reperiri poteſt abſ〈que〉 alijs centris; at non è conuerſo.
Rurſus commune magis eſt centrum figuræ centro magnitu­
dinis; quia præter circulum, & ſphæram, quæ tam figuræ, quam
magnitudinis centrum habent, nonnullæ figuræ ſuum ha­
bent figuræ centrum in ipſis, & extra ipſas; in ipſis, vt ellipſis,
cuius centrum intùs habetur; ſemicirculus etiam, dimidia què
ſphæra centrum habent in limbo. extra figuram verò veluti
hyperbolæ centrum, quod extra figuram exiſtit; vbi nempè
diametri concurrunt. Quæ quidem omnia ſunt figuræ cen­
tra; magnitudinis verò minimè. verùm obijciet hoc loco for
1taſſe quiſpiam, vel ambas, inquiens, centri grauitatis defini­
tiones allatas, diminutas eſſe; vel ijs, quæ modò à nobis de cem
tro grauitatis dicta ſunt, repugnare; cùm oſtenderimus cen­
trum grauitatis aliquando eſſe, vel in ambitu figuræ, vel extra
figuram; definitiones verò allatę ſemper ſupponunt illud eſſe
in ipſis intra poſitum. Confirmaturquè difficultas, quandoqui­
dem, ne〈que〉 huiuſmodi centrum extra figuram conſtitutum,
fuiſſe Archimedi prorſus ignotum, exiſtimare debemus; vt
colligere licet ex nono poſtulato huius libri; cùm inquit.
Omnis figuræ, cuius perimeter ſit ad eandem partem concauus, centrum
grauitatis intra ipſam eſſe oportet. quaſi non repugnet figurę peri
metrum non ad eandem partem concauum habenti, extra
ipſam grauitatis centrum obtinere. Cui obiectioni in hunc
modum occurri poterit, ſi dixerimus, quòd quamuis exempli
gratia in figura C dictum ſit centrum grauitatis D extra fi
guram exiſtere, id ipſum etiam intra figuram eſſe affirmati
poterit. ſiquidem ambitus figurę C centrum D intra ſe com
tinct; ita vt reſpectu tötius ſit intra. idemquè dicendum eſt de
altera figura A. hoc autem euidentiſſimum eſt in figura E.
& hic eſt ſenſus definitionum centri grauitatis. His ita〈que〉 pri
mùm cognitis conſideranda eſt intentio Archimedis in his li
bris, quę quidem vt plurimum à librorum inſcriptionibus e­
luceſcere ſolet.
5[Figure 5]
DE SCOPO HORVM LIBRORVM
Si Archimedis propoſitum in his libris ex ipſa operis in­
ſcriptione, vt in alijs quo〈que〉 aliorum authorum volumini­
bus fieri vt plurimùm ſolet, inueſtigandum erit, partim ſanè
conſpicuum illud eſſe videbitur, partim verò ignotum adeò,
vt potiùs nullius fermè rei ſe habiturum eſſe ſermonem profi­
teatur Archimedes. quid enim (obſecro) verbis illis ſignificari
potuit, 〈que〉 primi libri initio ita ſe habent. Aρχιμήδους ἐπιπέδων ἰσορ­
ροπιχω̄ν, ὴ κέντρα βάρων ἐπιπέδων. hoc eſt. Archimedis planorum æ〈que〉pon
derantium, vel centra grauitatum planorum. quando quidem vide­
tur Archimedes rem prorſus inutilem, quinnimò naturę repu­
gnantem ſibi contemplandam proponere. dùm enim
1cetur ſe eſſe pertractaturum de planis æquæponderantibus, ſi
ue de centris grauitatum planorum; cùm ea, quæ æ〈que〉ponde
rare debent, ponderare quo〈que〉 oporteat; ſi plana æ〈que〉ponde
rare debent, grauitate quadam illa prædita eſſe neceſſe eſt. quod
valdè à planorum natura abhorret, cùm grauitas, nonniſi cor
poribus, ne〈que〉 tamen omnibus competat. ipſe tamen, dum
plana æ〈que〉ponderantia, vel centra grauitatum planorum ſe
explicaturum pollicetur, apertè ſupponit plana, ac ſuperficies
graues exiſtere, rem ſanè immaginariam prorſus, ipſiusquè rei
naturæ nullatenus reſpondentem. ita vt Archimedes circa ea,
quæ omnino rei naturæ aduerſantur, negotium ſumpſiſſe vi­
deatur. Verùm enimuero ſi Authoris mentem acuratiùs intuea
mur, rem planè egregiam, naturæquè rei apprimè conſenta­
neam ipſum pertractandam ſumpſiſſe depræhendemus. Nam
quamuis plana, quatenus plana ſunt, nullam habeant graui­
tatem, non eſt tamen à rei natura, ne〈que〉 à ratione alienum,
quin poſſimus planorum, ſuperficierum què centra grauitatis
depræhendere, ex quibus ſi ſuſpendantur, planorum partes
vndiquè ęqualium momentorum conſiſtentes maneant. quan
doquidem centrum grauitatis talis eſt naturæ, vt ſi mente con­
cipiamus, rem aliquam in eius centro grauitatis appenſam eſ­
ſe, eo prorſus modo, quo reperitur, quieſcat, & maneat. vt
antea declarauimus. & quamuis re ipſa, actù〈que〉 plana ſeorsum
à corporibus reperiri ne〈que〉ant; in ipſis tamen hæc ipſorum
circa centra grauitatis æ〈que〉ponderatio ad actum facilè redigi
poterit. Vt ſit ſolidum AB priſ­

ma, cuius latera AE CF DB ſint
horizonti erecta, ſuperiorquè ba­
ſis ACD, 〈que〉m ad modum & in­
ferior EFB ſit horizonti æquidi­
ſtans; ſit autem plani ACD cen­
trum grauitatis G, ex quo G ſi
ſuſpendatur totum AB patet
planum ACD horizonti æqui­
diſtans permanere, ac propterea
circa centrum grauitatis G æ〈que〉­
ponderare. quod quidem, quamuis egeat demonſtratione,
1 in præſentia omittatur; infraquè ſuo loco oſtendendum. ſat
autem nobis nunc ſit oſtendiſſe, hæc ad praxim reduci, ma­
nibuſquè (vt dicitur.) contrectari poſſe. Quòd ſi hæc ita ſe ha
bent, huiuſmodi conſideratio non erit vana, ne〈que〉 vt inuti­
lis reijcienda. Sed vlteriùs adhuc progrediamur, dicamuſ­
què, quoniam planum ACD, quatenus eſt corpori coniun­
ctum, horizonti æquidiſtans permanere debet; ſi ſeorſum à
corpore illud intelligamus, vt ſi ADC ex eius centro graui­
tatis G ſuſpendatur, tunc quocun〈que〉 modo reperiatur, hoc
eſt ſiue horizonti ęquidiſtans, ſiuè
minùs, idipſum permanſurum ni

hilominus intelligere poſſumus,
parteſquè vndi〈que〉 æqualium mo
mentorum conſiſtentes. Ne〈que〉
enim Ariſto teles grauibus dunta­
xat, ſed etiam leuibus momenta
tribuit, idipſum què (vt Eutocius
in horum librorum comentarijs
refert) Ptolæmeo quo〈que〉 placuit, vt habetur in líbro (à nobis
ramen deſiderato) 〈que〉m de momentis ſcripſit. Pręterea alij­
quo〈que〉 Philoſophi id ipſum ſenſiſſe videntur. quod eſt qui­
dem rationi conſentaneum, ſuperuolant enim, quæ leuia ſunt,
& ſi mente concipiatur eadem figura leuis cuiuſpiam eſſe, tunc
ſi detineatur in G, partes vndi〈que〉 ęqualium momentorum
conſiſtent, eſſetquè G (vt ita dicam) centrum leuitatis. Quo­
niam autem circa centrum grauitatis ę〈que〉ponderationem
conſideramus, id circo plana, tanquam no bis apparentia gra­
uitatem habere, mente concipimus. Non eſt igitur à ratio­
ne alienum, æ〈que〉ponderantiam in planis, vt grauibus conſi­
deratis intelligere, conciperequè. Nec quicquam nobis offi­
cit, quòd definitiones centri grauitatis priùs allatæ non pla­
norum, ſed corporum centra explicarunt, ita vt grauitatis cen­
trum ad corpora, non ad plana ſit referendum. Hoc enim ideo fa
ctum eſt, quia propriè centrum grauitatis reſpicit corpora; non ta
men propterea impropriè reſpicit plana, ſed quia primò reſpi
cit corpora; in quibus actu ineſſe depræhenditur. propterea eędem­
met definitiones planis quo〈que〉 in hunc modum aptari poterunt.
1
in fine pri­
mi libri.
6[Figure 6] 7[Figure 7]
DEFINITIO CENTRI GRAVITATIS PLANORVM.
Centrum grauitatis vniuſcuiuſ〈que〉 plani eſt punctum quod­
dam intra poſitum, à quo ſi planum appenſum mente con­
cipiatur, dum fertur, quieſcit; & ſeruat eam, quam in princi­
pio habebat poſitionem, ne〈que〉 in ipſa latione circumuertitur.
EIVSDEM ALIA DEFINITIO.
Centrum grauitatis vniuſcuiuſ〈que〉 plani eſt punctum il­
lud intra poſitum, circa quod vndi〈que〉 partes æqualium mo
mentorum conſiſtunt. ſi enim per tale centrum recta du­
catur linea figuram quomodocun〈que〉 ſecans, ſemper in par
tes æ〈que〉ponderantes ipſam diuidet.
Vt Ita〈que〉 in planis quo〈que〉 centrum grauitatis conſide­
ratur, ita etiam plana grauitate prædita conſiderare, non e­
rit abſurdum. ſi enim impoſſibile eſſet conſiderare plana gra
uitate prædita, centrum quo〈que〉 grauitatis in ipſis nullo mo­
do concipi poſſet; at〈que〉 perſpicuum eſt, centrum grauitatis in
ipſis admitti, ac deſignari poſſe, igitur & plana grauitate inſi
gnita. Et ſi mathematicus conſiderat corpora ſecluſa interim
ipſorum grauitate, & leuitate: & Aſtronomus corpora conſi­
derans cæleſtia, quæ ne〈que〉 grauia, ne〈que〉 leuia ſunt, non pro­
pterea conſiderat ea ex propria ipſorum natura, ne〈que〉 grauia, ne
〈que〉 leuia eſſe; etenim quamuis grauia, vel leuia eſſent, nihilo
minus ne〈que〉 grauia, ne〈que〉 leuia eſſe ea conſideraret. quòd ſi
Mathematicus hoc pacto huiuſmodi corpora intelligere po­
teſt; quid prohibet rurſum eadem, quamuis vt talia, ne〈que〉 grauia,
ne〈que〉 leuia ſint; vel grauia, vel leuia eſſe concipere? 〈que〉mad­
modum hoc quo〈que〉 exem

plo res magis eluceſcet:
veluti ſi intelligamus ex
AC appenſa eſſe plana
DE, quæ ſint æqualia; ſu
ſpendaturquè AC in me
dio prorſus in B; cur mente intelligere non poſſumus,
quantitatem, ſpaciumquè D æ〈que〉ponderare ſpacio E; cùm ſint æqua
lia? ſi planorum alterum, putà D, maius eſſet ipſo E; tunc
1ſtatim non ſolùm ę〈que〉ponderare non poſſe, verùm etiam pla
num D deorſum tendere concipiemus. & hoc nulla alia de
cauſa, quàm quòd cùm D maius ſit, quàm E, ſtatim ipsum
D, quàm E grauius quo〈que〉 eſſe concipimus. Conſiderare
igitur plana cum grauitate non eſt omnino à ratione alienum.
Quare vtrum 〈que〉 titulum, nempe planorum æ〈que〉ponderan
tium, vel centra grauitatis planorum, admittendum duximus.
Verùm quoniam Archimedes ſecundum librum ſimplici vo
cabulo, nimirum (quaſi ſimul omnia complectens) æ〈que〉pon­
derantium in ſcripſit; idcirco tam primum, quàm ſecundum li
brum (æ〈que〉ponderantium) inſcribendum exiſtimamus. eo­
què libentiùs; quoniam ipſemet Eutocius horum quo〈que〉 li­
brorum explanator hoſce libros hoc tantùm nomine æ〈que〉­
ponderantium nuncupauit: alijquè omnes, qui hos Archime
dis libros nominant; hoc titulo de æ〈que〉ponderantibus nun
cupant. Præterea titulus hic magis operi congruere mihi vide
tur; quoniam nonnulla Archimedes in principio pertractat,
quæ tam ſolidis, quàm planis communia exiſtunt; quamuis
cætera ad plana ſint tantum referenda. in quibus omnibus de re
admodum vtili, & ad quamplurima conduencti pertractat. quandoqui
dem ex ijs, quæ ab Archimede his libris docemur, in multarum re­
rum cognitionem peruenire poſſumus. quod facilè conſtat inpri
mis ipſiuſmet Archimedis exemplo. ſiquidem hac methodo ipſe
in libro de quadratura paraboles comparando plana in libra com
ſtituta, ipſius paraboles quadraturam miro artificio adinuenit.
Deinceps ex cognitione centrorum grauitatis planorum, nos in
cognitionem centrorum grauitatum ſolidorum deducimur.
Deni〈que〉 adeo proficua eſt hæc doctrina, quam nobis in his
libris Archimedes præſtat; vt affirmare non verear, nullum
eſſe Theorema, nullum què problema ad rem mechanicam
pertinens, quod in ſui ſpeculatione peculiare non aſſumat fun
damentum ex ijs, quæ Archimedes in his libris ediſſerit. 〈que〉m­
admodum (cæteris interim omiſſis) patet ex vulgata illa pro­
poſitione enunciante, ita ſe habere pondus ad pondus, vt di
ſtantia ad diſtantiam permutatim ſe habet, ex quibus ſuſpen
duntur. quæ præclariſſimè ab ipſo in primo libro demonſtra
tur. Et quamuis Iordanus Nemorarius (〈que〉m ſecutus eſt
1Nicolaus Tartalea, & alij) in libello de ponderibus hanc ean­
dem propoſitionem quo〈que〉 demonſtrare conatus ſit; & ad
cam oſtendendam pluribus medijs fuerit vſus; nulli tamen pro
bationi demonſtrationis nomen conuenire poteſt. cùm vix
ex probabilibus, & ijs, quæ nullo modo neceſſitatem afferunt,
& fortaſſe ne〈que〉 ex probabilibus ſuas componat rationes.
Cùm in mathematicis demonſtrationes requirantur exquiſi­
tiſſimæ. ac propterea ne〈que〉 inter Mechanicos videtur mihi
Iordanus ille eſſe recenſendus. Quapropter ad Archimedem
confugiendum eſt, ſi fundamenta mechanica, veraquè huius
ſcientiæ principia perdiſcere cupimus: qui (meo iudicio) ad
hoc potiſſimùm reſpexit; vt elementa mechanica traderet. vt
etiam Pappus in octauo Mathematicarum collectionum li­
bro ſentit; quod quidem ex diuiſione, ac progreſſu horum li­
brorum facilè dignoſcetur.
8[Figure 8]
DE DIVISIONE HORVM LIBRORVM.
Diuiditur enim in primis hic tractatus in duos libros diui­
ſus, in poſtulata, & theoremata: theoremata verò ſubdiui­
duntur in duas ſectiones, quarum prima continet priora o­
cto theoremata; ad alteram verò reliqua theoremata ſpectant.
quæ quidem adhuc in alias duas partes diuidi poteſt; nempè
in theoremata primo libro examinata, & in ea, quæ ſecun­
dus liber contemplatur. Hanc autem horum librorum con
ſtituimus diuiſionem, quoniam imprimis Archimedes, (o­
miſſis poſtulatis, quæ primum locum obtinere debent) quæ­
dam tractauit communia in prioribus octo theorematibus;
quorum ſcopus eſt inuenire fundamentum illud præcipuum
mechanicum, quòd ſcilicet ita ſe habet grauitas ad grauita­
tem, vt diſtantia ad diſtantiam permutatim. ad quod demon
ſtrandum quin〈que〉 præmittit theoremata, quæ paulatim
deducunt nos in cognitionem demonſtrationis præfati fun
damenti. quo loco illud ſummoperè notandum eſt, nimi­
rum fundamentum illud, nec non octo priora theorema­
ta communia eſſe tam planis, quàm ſolidis; at〈que〉 promiſ­
cuè de vtriſ〈que〉 Archimedem demonſtrare. quòd ſi quis aliter
1ſenſerit, demonſtrationeſquè tantùm de planis concludere exi
ſtimauerit, vel de ſolidis, non autem quibuſcun〈que〉, ſed vel de
rectilineis, vel de homogeneis tantùm, & de ijs, quæ inter ſe
ſunt eiuſdem ſpeciei, longè aberrat à ſcopo, & mente Archi­
medis. etenim in his ſemper loquitur. vel de grauibus ſimpli
citer, veluti in primis tribus theorematibus; vel de magnitu
dinibus, vt in reliquis quin〈que〉 quod quidem nomen tam
planis, quàm ſolidis quibuſcun〈que〉 eſt commune, vt etiam ij,
qui parùm in Mathematicis verſati ſunt, ſatis norunt. ſicu­
ti etiam Euclides, dum quinti libri propoſitiones pertracta­
uit, quantitatem continuam ſub nomine magnitudinis com
prehendit. quòd autem nomen grauis ſit commune, iam ſatis
per ſe conſtat. Perſpicuum eſt igitur priora hæc octo Theo
remata communia eſſe, tam planis, quàm ſolidis. ac non ſo­
lùm ſolidis eiuſdem ſpeciei, & homogeneis, verùm etiam ſoli
dis diuerſæ ſpeciei, & hęterogeneis, vt ſuo loco manifeſtum
fiet. Iactoquè hoc fundamento, quod Archimedes in duobus
propoſitionibus, ſexta nempè, & ſeptima demonſtrauit; in o­
ctaua tanquam corrollarium colligit. Deinceps peculiariter
pertractat de centro grauitatis planorum, nec amplius plana
nominat magnitudinis nomine, ſed proprijs cuiuſcun〈que〉
nominibus; vt parallelogrammi, trianguli, & aliorum huiuſ­
modi. & in hac parte deſcendit ad particularia. quippè cùm
& ſi non actu fortaſſe, virtute tamen cuiuſlibet particularis
plani centrum grauitatis nos doceat. in primo enim libro
ſat ſi bi viſum eſt oſtendiſſe centra grauitatum triangulorum,
ac parallelogrammorum, ex quibus cæterarum figurarum,
veluti pentagoni, hexagoni, & aliorum ſimilium centra gra­
uitatis inueſtigare non admodum erit difficile. ſiquidem hu
iuſmodi plana in triangula diuiduntur. vt in ſine primi li­
bri attingemus. In ſecundo autem libro altiùs ſe extollit, &
moro ſuo circa ſubtiliſſima theoremata verſatur; nempè cir
ca centrum grauitatis conice ſectionis, quæ parabole nun­
cupatur. nonnullaquè præmittit theoremata, quæ ſunt tan­
quam præuie diſpoſitiones ad inueſtigandam demonſtra­
tionem centri grauitatis in parabole. Ita〈que〉 perſpicuum eſt,
Archimedem propriè elementa mechanica tradere.
1quidem duo pertractat, quæ ſunt tanquam elementa huius
ſcientiæ. fundamentum nempè illud præſtantiſſimum iam
toties præfatum, deinde centra grauitatis planorum oſtendit.
& quamuis hi duo Archimedis libelli pauca continere videan
tur, non tamen pauca docuiſſe Archimedem exiſtimandum
eſt. multa enim ſunt mole exigua, quæ tamen virtute maxima
habentur. quod planè Archimedis ſcriptis accidit; hiſquè prę
ſertim, ex quibus patet aditus ad multa, ac penè infinita theo­
remata, problemataquè mechanica. nihil enim in hoc gene­
re demonſtrari poteſt, quod his non indigeat ſcriptis. &
quod admirabilius eſt, nos non ſolùm pro fundamento ſu­
ſcipere poſſe ad aliquod demonſtrandum theoremata in his
libris demonſtrata, verùm etiam ab his demonſtrationibus
perdiſcerere ipſum modum argumentandi, & demonſtrandi;
vt ſuis locis oſtendemus. ita vt verè concludendum ſit, nemi­
nem prorſus inter mechanicos connumerandum fore, qui
hæc Archimedis ſcripta ignorat. ignoratis enim principijs
nulla eſt ſcientia, vt apud omnes ſapientes perſpicuum eſt.
Ipſum igitur Archimedem audiamus, eiuſquè ſcripta diligen
tiſſimè perpendamus.
1
[Empty page]
1
GVIDIVBALDI
EMARCHIONIBVS
MONTIS.
IN PRIMVM ARCHIMEDIS
AEQVEPONDERANTIVM
LIBRVM
PARAPHRASIS
SCHOLIIS ILLVSTRATA.
Archimedis tamen huius primi libri
titulus ſic ſe habet.
ARCHIMEDIS PLANORVM AEQVEPONDERANTIVM,
VEL CENTRA GRAVITATVM PLANORVM.
9[Figure 9]
ARCHIMEDIS POSTVLATA.
I.
Grauia æqualia ex æqualibus diſtantijs æ〈que〉­
ponderare.
SCHOLIVM.
Dvobvs modis grauia in diſtantijs
collocata intelligi poſſunt. quod &
in cæteris poſtulatis, & in propoſi­
tionibus intelligendum eſt. etenim
vel grauia sunt appenſa, vt in prima fi­
gura æqualia grauia AB ſunt in CD
appenſa; ita vt diſtantia EC ſit di­
ſtantiæ ED æqualis. intelligaturquè
CD tanquam libra, quæ ſuſpendatur
in E. vel vt in ſecunda figura grauia AB habent ipſorum
centra grauitatis, quæ ſint CD, in ipſa DC linea, in
1ctis nempè CD

conſtituta. li­
braquè ſimili­
ter ex puncto
E ſuſpendatur;
ſitquè diſtantia
EC diſtantiæ
ED æqualis.
erunt vti〈que〉 in
vtra〈que〉 figura
pondera AB
in diſtantijs ę­
qualibus con­
ſtituta. ac pro­
pterea æ〈que〉ponderabunt, at〈que〉 manebunt. nulla enim ratio
afferri poteſt, cur ex parte A, vel ex parte B deorſum, vel ſur
ſum fieri debeat motus; cùm omnia ſint paria. ea verò æ〈que〉­
ponderare debere, aliqua ratione manifeſtari poteſt ex eo,
quod oſtenſum eſt à nobis in noſtro mechanicorum libro,
tractatu de libra: quod quidem ab Ariſto tele quo〈que〉 in prin
cipio quæſtionum mechanicarum elici poteſt: idem ſcilicet
pondus longius a centro grauius eſſe eodem pondere ipſi cen
tro propinquiori. Vnde ſi duo eſſent pondera æqualia alte­
rum altero propinquius centro, quod remotius eſt, grauius al
tero appareret. ſi igitur grauia æqualia à centro æqualiter di­
ſtabunt, æ〈que〉 grauia erunt. ac propterea æ〈que〉ponderabunt.
quod quidem ſupponit Archimedes. Punctum autem illud,
quod Archimedes accipit, vnde ſumuntur diſtantiæ, ex qui­
bus grauia ſuſpenduntur, veluti punctum E, Ariſtoteles cent
rum appellat. & hæc quidem æ〈que〉ponderatio tam ponderi­
bus in libra appenſis, quàm in ipſa (vt dictum eſt) conſtitutis
competit: dummodo ea, quibus appenduntur pondera, libe­
re ſemper in centrum mundi tendere poſſint. vtro〈que〉 enim
modo in punctis CD grauitant, vt diximus etiam in eodem
tractatu de libra. Nouiſſe tamen oportet Archimedem in his
libris potiùs intellexiſſe pondera eſſe in diſtantijs collocata, vt
in ſecunda figura, quàm appenſa; vt ex quarta, & quinta
1primi libri propoſitione pater. demonſtrationes enim cla­
riores redduntur.
10[Figure 10] 11[Figure 11]
Porrò non ignoran
dum hoc Archimedis
poſtulatum verificari
de ponderibus quocun
〈que〉 ſitu diſpoſitis, ſiue
CED fuerit horizonti
æquidiſtans, ſiuè minùs;
vt in hac prima figura,
codem modo ſemper
verum eſſe pondera æ­
qualia CD ex ęquali­
bus diſtantijs EC ED
æ〈que〉ponderare, vt in­
fra (poſt ſcilicet quartam
huius propoſitionem)
perſpicuum erit. Qua­
re cùm Archimedes tam
in hoc poſtulato, quam
in ſe〈que〉ntibus, ſuppo­
nit pondera in diſtan­
tijs eſſe collocata, intel­
ligendum eſt diſtantias
ex vtra〈que〉 parte in ea­
dem recta linea exiſte­
re. Nam ſi (vt in ſecun
da figura) diſtantia AB
fuerit ęqualis diſtantię BC, quæ non indirectum iaceant,
ſed angulum conſtituant; tunc pondera AB, quamuis ſint
ęqualia, non ę〈que〉ponderabunt. niſi quando (vt in tertia fi­
gura) iuncta AC, bifariamquè diuiſa in D, ductaquè BD,
fuerit hęc horizonti perpendicularis, vt in eodem tractatu
noſtro expoſuimus. Diſtantias igitur in eadem recta linea
ſemper exiſtere intelligendum eſt. vt ex demonſtrationibus
Archimedis perſpicuum eſt.
1
II.
Aequalia verò grauia ex inæqualibus diſtantijs
non æqueponderare, ſed præponderare ad gra­
ue ex maiori diſtantia.
SCHOLIVM.
Si enim diſtam

tia EC maior
fuerit diſtantia
ED, grauibus
AB ſimiliter æ­
qualibus exiſtem
tibus, & in CD poſitis, tunc concedendum videtur graue A
præponderare ipſi B, quandoquidem EC longior eſt, quàm
ED. ſupponit autem Archimedes hoc poſtulatum reſpiciens
fortaſſe ad ea, quæ Ariſtoteles in principio quæſtionum me­
chanicarum oſtendit, vbi colligit Ariſtoteles idem pondus ce­
leriùs ferri, quò magis à centro diſtat, vel quod idem eſt, duo
pondera æqualia inæqualiter à centro diſtantia, quod magis
diſtat, celeriùs ferri. quod autem æqualium ponderum cele­
riùs fertur, grauius exiſtit; erit igitur A grauius, quàm B.
quia EC longior eſt, quàm ED. Nos quo〈que〉 (vt diximus)
in libro noſtrorum Mechanicorum tractatu de libra, alijs
quo〈que〉 rationibus oſtendimus, quo pondus eſt in longiori
diſtantia grauius eſſe. ex quibus ſequitur propter longiorem
diſtantiam EC pondus A præponderare ponderi B. ac pro­
pterea deorſum ferri.
12[Figure 12]
III.
Grauibus ex aliquibus diſtantijs æ〈que〉ponderan
tibus, ſi alteri grauium aliquid adijciatur, non æ­
〈que〉ponderare; ſed ad graue, cui adiectum fuit,
deorſum ferri.
1
SCHOLIVM
Grauia enim

AB ſiuè æqua­
lia, ſiue in ęqua
lia æ〈que〉ponde
rent ex diſtan­
tijs AC CB, al­
teri verò gra­
uium, putà B,
adijciatur pon
dus D. perſpicuum eſt pondera BD ſimul magis ponderare,
quàm A. ſi enim B ę〈que〉ponderat ipſi A; erit pondus B in
hoc ſitu æ〈que〉graue, vt A: pondera igitur BD in hoc ſitu non
erunt æ〈que〉grauia, vt pondus A. ſed grauiora exiſtent, quàm
A. quare BD deorſum tendent.
13[Figure 13]
IIII.
Similiter autem, ſi ab altero grauium auferatur
aliquid, non æ〈que〉ponderare; verùm ad graue, à
quo nil ablatum eſt, deorſum tendere.
SCHOLIVM.
Ae〈que〉ponderent grauia BD ſimul, & A di­
ſtantias CB CA; vt in eadem figura, & ab altero eorum, putà
BD, auferatur D, remanebunt grauia BA; eritquè A gra­
uius ipſo B. Nam ſi BD ſimul æ〈que〉ponderant ipſi A, B
tantùm eidem A non æ〈que〉ponderabit, ſed leuius erit. vnde
ſequitur ex parte A motum fieri deorſum.
1
eadem figu
ra.
V
Aequalibus, ſimilibuſquè figuris planis inter ſe
coaptatis, centra quo〈que〉 grauitatum inter ſe coa­
ptati oportet.
SCHOLIVM.
Aequales, ſimiles〈que〉; ſint

figuræ ABC DEF, qua­
rum centra grauitatis ſint
GH; ſi ABC ſuperpona­
tur ipſi DEF, & hoc ſecum
dùm laterum æqualitatem,
hoc eſt ſi latus AB fuerit
æquale lateri DE, tunc
ponatur AB ſuper DE; ſimiliter AC ſuper DF, & BC ſuper
EF; tunc manifeſtum eſt centrum grauitatis G ſuper centro
grauitatis H ad unguem conuenire; ita vt ſint vnum tan tum
punctum. Plana enim quæ ſe inuicem contingunt, non ef­
ficiunt, niſi vnum tantùm planum. Solius autem figuræ ex
planis ABC DEF inuicen coaptatis, vnum tantùm erit cen
trum grauitatis, vt nos in noſtro mechanicorum libro ſup­
poſuimus; centra igitur grauitatis inter ſeſe conuenire neceſ­
ſe eſt. ſi enim centra grauitatis inter ſe non conuenirent, v­
na tantùm figura duo poſſet centra grauitatis habere. quod
eſſet omnino inconueniens. Dixit autem Archimedes oporte
re has figuras eſſe ſimiles, & æquales, nam figuræ æquales,
ſed non ſimiles, item ſimiles, & non æquales eſſe poſſunt. qua­
re, vt inter ſeſe coaptari poſſint, & ſimiles, & æquales eſſe ne­
ceſſe eſt.
14[Figure 14]
VI
Inæ qualium autem, ſed ſimilium centra graui­
tatum eſſe ſimiliter poſita.
1
SCHOLIVM.
Inæquales ſint figuræ, ſi­

miles verò ABCD EFGH,
quarum cétra grauitatis ſint
KL. ſupponit Archimedes
hęc grauitatis centra KL eſ­
ſe in figuris ABCD EFGH
ſimiliter poſita. cùm enim
ſimilium figurarum, & late­
ra, & ſpacia ſint ſimilia, neceſſe eſt in ipſis ſimili quo 〈que〉 mo­
do centra grauitatis eſſe poſita. vt in ſe〈que〉nti clariùs apparebit.
quomodo autem Archimedes intelligat hanc poſitionis ſimi­
litudinem, hoc modo definit.
15[Figure 15]
VII.
Dicimus quidem puncta in ſimilibus figuris eſ­
ſe ſimiliter poſita, à quibus ad æquales angulos
ductæ rectæ lineæ cum homologis lateribus angu
los æquales efficiunt.
SCHOLIVM.
In ſimilibus figuris ABCD EFGH ſint homologa latera
AB EF, BCFG, CD GH, AD EH. anguli verò æquales, qui
ad AE, BF, CG, DH, primum quidem oſtendendum eſt fie
ri poſſe, ut à duobus punctis intra figuras conſtitutis, duci
poſſint rectę lineę ad angulos æquales, quę cum lateribus an­
gulos ęquales efficiant. Quaſi dicat Archimedes, quoniam
ſupponere poſſumus puncta in ſimilibus figuris eſſe ſimiliter
poſita, ideo ſupponere quo〈que〉 poſſumus centra grauitatis in
ipſis eſſe ſimiliter poſita. Ita〈que〉 ſint figuræ ABCD EFGH ſi­
miles, vt dictum eſt, ſumaturquè in ABCD vtcum〈que〉 pun­
ctum K à quo ducatur KA KB KC KD. deinde fiat an
1
gulus FEL angulo BAK æqualis; & EFL ipſi ABK. Iun
ganturquè GL LH. Dico L eſſe ſimiliter poſitum, vt K.
Quoniam enim anguli BAK ABK ſunt angulis FEL EFL
æquales, erit reliquus BKA ipſi FLE æqualis, eritquè ob ſi­
militudinem triangulorum KA ad AB, vt LE ad EF. eſt
verò AB ad AD, vt EF ad EH propter ſimilitudinem fi­
gurarum, erit igitur ex æquali AK ad AD, vt LE ad EH,
& quoniam angulus BAD angulo FEH eſt æqualis, & BAK
ipſi FEL æqualis; erit & reliquus angulus KAD angulo
LEH æqualis. Quare triangulum KAD triangulo LEH ſi
mile exiſtit, eodemquè modo oſtendetur BKG ſimile eſſe
FLG, & KCD ipſi LGH. ex quibus conſtat angulos KBC
LFG, KCB LGF, & huiuſmodi reliquos reliquis æquales eſſe.
& ob id puncta KL in figuris ABCD EFGH eſſe ſimili­
ter poſita.
4 ſexti.
22 quinti.
6 ſexti.
16[Figure 16]
Ita〈que〉 demonſtrato dari poſſe puncta in figuris ſimiliter
poſita, potuit ſanè Archimedes antecedens poſtulatum ſup­
ponere, nempè inæqualium, ſed ſimilium figurarum centra
grauitatis eſſe ſimiliter poſita. quod quidem poſtulatum eſt
rationi valde conſentaneum. ex dictis enim (ſuppoſitis KL
centris grauitatum) triangulum ABK triangulo EFL ſimi­
 le exiſtit; veluti BKC ipſi FLG. & reliqua reliquis. Quare vt
AK ad KB, ſic EL ad LF, ac permutando vt AK ad EL,
ita BK ad FL. ſimiliter oſtendetur ita eſſe BK ad FL, vt
KC ad LG, & KD ad LH. quare centra grauitatis KL
1proportionaliter ab angulis diſtant.
4 ſexti
16 quinti
Ducantur pręterea à punctis KL ad latera perpendiculares
KM KN KO KP, LQ LR LS LT. & quoniam anguli
KMA LQE ſunt recti, ac propterea æquales, & KAM LEQ
ſunt æquales, ut oſtenſum eſt; erit reliquus MKA reliquo
QLE ęqualis, triangulumquè AKM triangulo ELQ ſimile.
vt igitur AK ad KM; ſic EL ad L〈que〉 & permutando
ad EL, vt KM ad L〈que〉 pariquè ratione oſtendetur triangu
lum BKM triangulo FLQ ſimile exiſtere; eſſequè BK ad
FL, vt KM ad L〈que〉 ſimiliterquè in alijs triangulis oſten­
detur, ita eſſe Bk ad FL, vt KN ad LR; & Ck ad GL eſſe, vt
kO ad LS; at〈que〉 kD ad LH, vt kP ad LT. quia verò AK
EL, Bk FL, Ck GL, Dk HL in eadem ſunt proportione, vt
proximè demonſtratum fuit; in eadem quo〈que〉 proportione
erit kM ad LQ, & KN ad LR; & KO ad LS, at〈que〉 kP ad
LT. ex quibus ſequitur centra grauitatis KL, non ſolùm ab
angulis in eadem proportione diſtare; verùm etiam à late­
ribus in eadem quo〈que〉 proportione diſtare. Ita〈que〉 cognito,
quomodo intelligar Archimedes centra grauitatis in ſimili­
bus figuris eſſe ſimiliter poſita; nunc conſiderandum eſt præ
cedens poſtulatum, quatenus nimirum oporteat grauitatis cem
tra in ſimilibus figuris ſimiliter eſſe conſtituta. Nam inti­
miùs conſiderando hanc ſimilem horum grauitatis centrorum
poſitionem, congruum, & neceſſarium videtur, ſimiles figu­
ras ſecundùm eandem proportionem eſſe æ〈que〉ponderantes;
eademquè ratione (ob earum ſimilitudinem) circa grauita­
tis centra æ〈que〉ponderare, veluti ſi figuræ: AC EG (quarum
centra grauitatis ſint KL) à rectis lineis PN TR vtcumquè
diuidantur, quæ per centra KL tranſeant; dummodo in figu
ris ſint ſimiliter ductæ; hoc eſt, vel latera, vel angulos in eadem
proportione diſpeſcant: vt ſit AP ad PD, vt ET ad TH. æ­
〈que〉ponderabunt vti〈que〉 partes PABN PNCD, veluti partes
TEFR TRGH. & hæc non eſt ſimplex æ〈que〉ponderatio; ve­
rùm etiam (vt ita dicam) ſimilis, & æqualis æ〈que〉ponderatio.
cùm ſit ſecundùm eandem proportionem, quandoquidem
eſt PB ipſi TF ſimilis, cùm triangula AKB ELF, AKP ELT,
BKN FLR, ſint inter ſe ſimilia, quæ quidem efficiunt, figuras
1PB TF inter ſe ſimiles eſſe. ob eademquè cauſam eſt PC ſi­
milis TG. quod quidem ex demonſtratis etiam facilè con­
ſtat. cùm anguli ſint ęquales, & latera proportionalia. Vt au­
tem clariùs intelligatur hæc ſimilis, & æqualis æ〈que〉pondera
rio, adducere libuit nonnulla ex ijs, quæ poſteriùs tractanda
ſumentur. Ita〈que〉 intelligatur punctum V centrum eſſe gra­

uitatis figuræ PB, X verò centrum grauitatis figure TF. ſi
militer punctum Y centrum eſſe grauitatis figuræ PC, Z
verò figurę TG. Iunganturquè VY XZ. quæ quidem per
centra grauitatis KL tranſibunt. quòd ex ijs, quę dicenda
ſunt, manifeſtum erit, percipuè〈que〉 ex octaua proportione
primi huius. quod tamen interim ſupponatur. At verò quo­
niam PB PC ę〈que〉ponderant ſecundùm proportionem,
quam habet YK ad KV; TF verò & TG ę〈que〉ponderant
ſecundùm proportionem, quam habet ZL ad LX. eſt. enim
ac ſi AN eſſet appenſa in V, & PC in Y; ER in X, &
TG in Z. vt in ſe〈que〉ntibus manifeſta erunt. Atverò quo­
niam AN ſimilis eſt ipſi ER, habebit AN ad ER duplam
proportionem eius, quam habet latus PN ad TR. pariquè
ratione quoniam PC ſimilis eſt TG, habebit PC ad TG
duplam proportionem eius, quam habet idem latus PN ad
TR. quare ita ſe habet AN ad ER, ut PC ad TG. & per­
 mutando AN ad PC, vt ER ad TG. Sed vt AN ad PC, ita eſt
Y K ad KV, & vt ER ad TG. ſic ZL ad LX. eandem igitur
1proportionem habebit YK ad KV, quam ZL ad LX. Quare
AN PC, & ER TG ſecundùm eandem proportionem æ­
〈que〉ponderabunt. quod quidem contingit ex ſimilitudine fi­
gurarum, & ex centris grauitatum KL ſimiliter poſitis, quę
quidem magnitudines, ſi non eſſent ſimiles, diuiſę quidem per
centrum grauitatis, partes vti〈que〉 ę〈que〉ponderarent; non ta­
men ſemper ſecundùm eandem proportionem. quod tamen
ſemper figuris ſimilibus (cùm in ipſis grauitatis centra ſint ſi
militer poſita) contingit; dummodo (vt dictum eſt) diui­
dantur. Vnde conſtat, quam ſit conueniens grauitatis centra
in figuris hac ratione eſſe conſtituta. ex quibus omnibus per
ſpicuum eſt, centra grauitatis debere in figuris ſimilibus eſſe ſi
militer poſita. vt Archimedes in pręcedenti poſtulato pręmiſit.
4 ſexti
16 quinti
20 ſexti
11 quinti
16 quinti
17[Figure 17]
VIII.
Si magnitudines ex æqualibus diſtantijs æ〈que〉­
ponderant, & ipſis æquales ex ijſdem diſtantijs æ­
〈que〉ponderabunt.
SCHOLIVM.
Hoc eſt perſpicuum, nam

ſi magnitudines AB ex di­
ſtantijs CA CB ę〈que〉pon­
derant: ſit autem D ipſi A
ęqualis, & E ipſi B. auferam
turquè magnitudines AB à
linea AB, ipſarumquè loco ponatur D in A, & E in B, ma
gnitudines DE ſimiliter ę〈que〉pondęrabunt. qua ratione enim
magnitudines AB inter ſeſe ę〈que〉ponderare dicuntur; eadem
prorſus, & magnitudines DE ex ijſdem diſtantijs ę〈que〉pon
derabunt. quandoquidem omnia data ſunt paria. illud ta­
men non eſt pretereundum, nimirum non oportere DE ipſis
AB ęquales eſſe in magnitudine, ſed in grauitate. poteſt enim
1magnitudinum inęqualium minor maiore grauior exiſtere,
ob naturæ diuerſitatem, ac propterea cùm inquit Archimedes
& ipſis aquales, ſiue ſint magnitudine æquales, vel inæquales, in
telligendum eſt eſſe omnino æquales in grauitate. grauitas. enim
cauſa eſt, vt magnitudines æ〈que〉ponderare debeant.
18[Figure 18]
VIIII,
Omnis figuræ, cuius perimeter ſit ad eandem par
tem concauus, centrum grauitatis intra figuram
eſſe oportet.
SCHOLIVM.
19[Figure 19]
Quid intelligat Ar­
chimedes per has figu­
ras ad eandem partem
concauas, apertiùs ſi­
gnificauit initio libro­
rum de ſphęra, & cylin­
dro. vbi primùm vult
has figuras eſſe termina
tas; quod non ſolùm in
telligendum eſt decur­
uilineis, verùm etiam
de rectilineis, & de mi­
xtis. rectilineę quidem
erunt trium, quattuor,
quin〈que〉 & plurium la­
terum; quamuis latera
non ſint æqualia, ne­
〈que〉 anguli ęquales, vt
1ABCDE, cuius omnes anguli ſunt flexi ad interiorem figuræ
partem. & hoc modo perimeter huius figuræ erit ad eandem
partem concauus. vnde excluduntur figuræ, exempli gratia
FGHKL; cùm angulus K non ſit ſinuoſus, & concauus ad
eandem partem, vt reliqui anguli; qui ſunt ſinuoſi verſus inte
riorem partem figurę K vero ad exteriorem. ſimili modo
intelligendum eſt de curuilineis, vt circuli, ellipſes, vel alterius
generis figuræ, vt ſunt MN, quæ ſuam habent concauitatem
ad eandem partem: ſed curuline˛ OP non ſunt ad eandem
partem concauę. Mixtæ quo〈que〉 figuræ, ut ſunt portiones cir
culi, hyperbolę ac parabolę rectis linenis terminatę, vel alte
rius generis figurę, vt ſunt QR. hę quidem omnes ſunt ad ean­
dem partem concauę. Mixtæ verò ST minimè Regulam au­
tem quandam vniuerſalem ex verbis Archimedis loco citato
elicere poſſumus, vt cognoſcere valeamus, an figuræ ſint ad
eandem partem concauæ, vel minùs vt ſcilicet in oblata figu
ra vbicum〈que〉 duo ſumi poſſint puncta, quæ ſi recta linea con
nectantur, tota recta li

nea, vel ipſius pars ali­
qua extra figuram non
cadat. vt in figuris A,
quæ ſunt ad eandem par
tem concauæ, vtcum­
〈que〉 duo ſumantur pun­
cta BC, quæ conne­
ctantur, tota uti〈que〉 re­
cta linea inter puncta
BC exiſtens, extra figu
ram non cadet. Quòd
ſi hæc linea cum termino, hoc eſt eum latere figurę conueni­
ret, vt ſi figuræ latus fuerit rectum, in quo duo ſumantur pun
cta, nihilominus recta linea inter hæc puncta extra figuram
non cadet: quandoquidem figuræ terminus extra figuram mi
nimè reperitur at〈que〉 hac ratione quomodocun〈que〉, & vbicum
〈que〉 in his figuris duo ſumantur puncta, idem ſemper contin
get. Quod tamen figuris D ſemper euenite non poteſt in qui
bus (cùm non ſint ad eandem partem concauę) duo ſumere
1poſſumus puncta EG, inter quę tota recta linea EG extra
figuram cadet. vel fumere poſſumus puncta FG, ita vt rectę
lineę FG pars EG extra figuram cadat. figurę igitur, quæ
ad eandem partem ſunt concauæ, illę ſunt, quę ſinuoſitatem,
concauitatemquè ſuam habent ſemper interiorem ipſius fi­
gurę partem reſpicientem. Harum què rectè ſupponit Archi­
medes centrum grauitatis ſemper eſſe intra ipſam figuram.
ita vt ne〈que〉 centrum eſſe poſſit in ambitu ipſius figurę ete­
nim ſi extra figuram, ſiue in ambitu ipſius eſſe poſſet, num­
quam circa centrum grauitatis partes figurę vndiquè ę〈que〉pon
derarent: ne〈que〉 facta ex grauitatis centro ſuſpenſione figura
vbicum〈que〉, & in omni ſitu maneret. quod ramen ex ratione
centri grauitatis efficere deberet. tota nimirum figura ex vna
eſſet parte, & ex altera nihil eſſet, quod ipſi figurę ę〈que〉ponde
rare poſſet. Neceſſe eſt igitur centrum grauitatis cuiuſlibet fi­
gurę ad eandem partem concauę eſſe in ſpacio à figurę ambi
tu contento. vt figurę AB

centrum grauitatis erit in­
tra ipſam, putà in C. quod
quidem non euenit ſemper
in alijs figuris, quę ſuum com
cauitatis ambitum interio­
rem figurę partem non reſpi­
cientem habent. cùm varijs
modis poſſit centrum graui
tatis in figuris eſſe collocatum.
vt ſuperius quo〈que〉 diximus.
Nam figurę D centrum gra­
uitatis erit extra ambitum fi
gurę, vt in E. figura verò F
ita ſe habere poterit, vt cen­
trum grauitatis ſit in perime
tro, vt in G. euenit autem aliquando vt in figura HK centrum
grauitatis L intra ipſam figuram reperiatur; quamuis conca­
uitates la torum interiorem partem minimè reſpiciant. Sed hęc
poſſunt eſſe, & non eſſe, vt in figura M, cuius centrum extra
eſſe poteſt in N. quamuis (vt antea diximus) centrum
1tatis intra figuram ſemper exiſtere aliquo modo intelligi po­
teſt.
per def.
cent. grau.
20[Figure 20] 21[Figure 21]
Refert Eutocius hoc loco, Geminum rectè dicere, dum aſſe­
rit Archimedem dignitates petitiones apellare. æqualia enim
grauia ex diſtantijs æqualibus æ〈que〉ponderare, dignitas eft; &
quæ deinceps. Verum ſi hæc principia ab Archimede tradita re
ctè perpendamus, omnia dignitates eſſe minimè reperiemus.
nam ſeptimum poſtulatum eſt definitio, non dignitas. veluti
alia fortaſſe nonnulla non ſunt dignitates, vt ſecundum; quod
aliquo modo probari poteſt, vt diximus. ſextum quo〈que〉 po­
tiùs eſt ſuppoſito, quàm dignitas. Quoniam autem vt clarè
conſpicitur Archimedes ſub vno tantùm titulo pauca hæc
principia complecti voluit; quippe quod inſtitutum quàm plu
rimis mathematicis ſolemne fuit, qui principia vnico tantum
nomine nuncuparunt, modò vno, modò altero; nimirum,
vel petitionis, vel dignitatis, vt refert Proclus ſecundo libro, &
tertio ſuorum commentariorum in primum elementorum. Eu
clidis; qui de Archimede peculiariter mentionem faciens, in­
quit illum in his libris principia vnico tantùm nomine (peti­
tionis ſcilicet) nuncupaſſe. Hæc tamen potiùs petitionum,
quàm definitionum, vel dignitatum nomine nuncupare vo­
luit; nam ſi dignitates appellaſſet; ea principia, quæ non ſunt
dignitates, inter dignitates malè collocaſſet. nulla quippè defi­
nitio dignitas dici debet; quandoquidem definitio terminos
declarat, at〈que〉 conſtituit. dignitas verò notos terminos copu­
lat. Pariquè ratione ſi definitionis nomine hæc principia nun
cupaſſet. dignitates malè ſub hoc nomine complexus fuiſſet,
quæ nullo modo rem definiunt, ſed cùm ſint communes no
tiones, ſtatim cùm eas intellectus apprehendit, quieſcit. Qua­
re omnia ſub petitionum nomine recte collocauit, non eſt. enim
abſurdum dignitates, definitioneſquè poſſe apellari petitio­
nes. etenim petimus, quæ ſunt concedenda, at〈que〉 dignitates
ſunt concedendę, ergo eas petere quo〈que〉 poſſumus. Definitio
nibus verò rectè quo〈que〉 hoc nomen conuenire poteſt. Nam
dùm definitio terminos conſtituat, at〈que〉 declaret, cur non pe
tere poſſumus, terminos ſic ſe habere, vel ſiceſſe rectè definitos?
vt exempli gratia, petit Archimedes puncta in figuris fimiliter
1poſita, ita ſehabere, vt ſunt ab ipſo definita, vel rectè eſſe defi­
nita puncta, quæ ſunt in figuris ſimilibus poſita. Quapropter
hæc principia, quoniam pauca ſunt, ſub petitionum nomine
Archimedes rectè collocauit. quòd ſi multa extitiſſent, ea for
taſſe diſtinxiſſet.
His ſuppoſitis. poſtquam Archimedes principia poſuit, ad theore
mata ſe conuertit, & inquit, his ſuppoſitis, quaſi dicat, ea, quæ
poſuimus, ſufficiunt ad oſtendenda theoremata, veluti.
PROPOSITIO. I.
Grauia, quæ ex æqualibus diſtantijs æ〈que〉pon­
derant, æqualia ſunt.
Sint AD, & B grauia,

quæ ex æqualibus diſtantijs
CA CB æ〈que〉ponderent. di
co grauia AD, & B inter­
ſeſe æqualia eſſe. ſi enim (ſi fie
ri poteſt) eſſent inæqualia; vt ſi
AD eſſet grauius, quàm B,
ſit D exceſſus, quo AD grauius eſt, quàm B. ablato ita〈que〉
exceſſu D à maiori AD, reliqua grauia, quæ relinquuntur AB,
erunt inter ſe ęqualia; quę ex ęqualibus diſtantijs CA CB æ­
〈que〉ponderare deberent; tamen non æ〈que〉ponderabunt. cùm enim
poſitum ſit AD B ę〈que〉ponderare, & ab altero a〈que〉ponderan-
tium AD aliquod ſit ablatum D; reliqua grauia AB ex ęqua
libus diſtantijs CA CB non ę〈que〉ponderabunt quod fieri
non poteſt; ſiquidem AB inter ſe ſunt ęqualia. Grauia igitur,
quæ ex æqualibus distantijs æ〈que〉ponderant, æqualia ſunt. quod de­
monſtrare oportebat.
4. poſtula­
tum huius
contra pri­
mum post
huius.
22[Figure 22]
SCHOLIVM.
Cùm ſit ſcopus Archimedis (vt diximus) in primis octo
theorematibus, fundamentum tradere in hac ſcientia
1puum, nempè magnitudinum grauitates inter ſe ita ſe habe­
re, vt diſtantiæ permutatim ex quibus ſuſpenduntur ſe habent.
primùm incipit oſtendere, quomodo ſe habeant grauia in di
ſtantijs ęqualibus poſita; primùmquè in hac prima propoſitio
ne oſtendit, ſi grauia ę〈que〉ponderant ex diſtantijs ęqualibus,
ęqualia eſſe. in ſe〈que〉nti verò, ſi grauia ſunt inęqualia, ex di­
ſtantijs ęqualibus nullo modo æ〈que〉ponderare oſtendet; ſed
præponderare ad maius.
PROPOSITIO. II.
Inæqualia grauia ex æqualibus diſtantijs non
æ〈que〉ponderabunt, ſed præponderabit ad maius.
23[Figure 23]
Sint gra­
uia inęqua­
lia AB C in
diſtantijs ę­
qualibus DA
DC. ſitquè
grauius AB,
quàm C. di
co grauia AB C non ę〈que〉ponderare, ſed maius AB deorsum
ferri. ſit B exceſſus, quo AB ſuperat C. ablato ita〈que〉 à ma
iori AB exceſſu B, reliqua grauia AC ęqualia ex diſtantijs
DA DC æ〈que〉ponderabunt. cùm æqualia grauia ex distantiis æquali-
bus æ〈que〉ponderent. ſi ita〈que〉 grauia AC ę〈que〉ponderant, adiecto
igitur ipſi A ablato B, præponderabit ad maius, hoc eſt ab
ſum tendet. quoniam æ〈que〉ponderantium altero nempè A adiectum
fuit B. Grauius igitur præponderat leuiori, ambobus in diſtan
tijs ęqualibus poſitis. quod demonſtrare oportebat.
1 poſt hu­
ius.
3 post hu­
ius.
SCHOLIVM.
Hæc duo theoremata in gręco exemplari impreſſo ſequun
tur quidem poſtulata, & reliquis theorematibus ſunt prępoſita.
1quia verò inter principia collocari non poſſunt; cùm ſuas ha­
beant propoſitiones, ſuaſquè ſeorſum habeant demonſtratio­
nes, ideo inter propoſitiones ipſa collocare nobis viſum eſt.
cùm pręſertim nonnulla ex ſe〈que〉ntibus theorematibus, po­
tiſſimùm verò proximum eiuſdem cum his duobus ordinis,
& naturæ ſint. Ne〈que〉 enim propterea peruertitur ordo; non
enim hę propoſitiones in alium transferuntur locum. ſed tan­
tùm inter alias numeris adnotantur. exiſtimandum enim eſt,
Archimedem propoſitiones in ſerie propoſitionum collocaſ­
ſe. hanc verò exiguam mutationem accidiſſe oblongitudinem
temporis; cuius proprium eſt, res potiùs deſtruere, quàm ac­
comodare. Hoc autem nobis hanc præbebit commoditatem,
vt, quando libuerit, has propoſitiones numeris nominare
poſſimus. id ipſumquè numeri poſtulata diſtinguentes præ­
ſtant, quamuis in Gręco codice poſtulata (Gręcorum more)
numeris adnotata non ſint.
PROPOSITIO. III.
Inæqualia grauia ex diſtantijs inæqualibus æ­
 〈que〉ponderabunt, maius quidem ex minori.
A
24[Figure 24]
Sint in æqualia grauia AD, B;
ſit què maius AD, exceſſus ve
rò, quo AD ſuperat B, ſit
D. æ〈que〉ponderentquè AD B ex
diſtantiis AC C B. oſtendendum
eſt, minorem eſſe diftantiam AC
ipſa CB. Non ſit quidem, ſi fie­
ri potest, AC minor, quàm CB; erit nimirum, vel ęqualis,
vel maior. Quòd ſi AC fuerit ęqualis ipſi CB, ablato enim
exceſſu D, quo AD ſuperat B. cùm ab a〈que〉ponderantium altero ab
latum ſit aliquid, grauia AB non æ〈que〉ponderabunt; ſed præ-
ponderabit ad B. non præponderabit autem; exiſtente enim AC aqua
li CB, cùm ab inęqualibus grauibus AD B ablatus ſit ex­
ceſſus D, grauia, quæ relinquuntur AB, erunt inter ſe æqualia;
1quæ ex diſtantiis æqualibus AC CB æ〈que〉ponderarent. at non ę〈que〉
ponderant, quod eſt abſurdum. diſtantia igitur AC ipſi CB
æqualis eſſe non poteſt. ſi uerò AC maior fuerit CB; ablato ſi­
militer exceſſu D, nihilominus ęqualia grauia AB non ę〈que〉
ponderabunt, ſed inclinabitur ad A. æqualia enim grauia AB ex
distantiis inæqualibus non æ〈que〉ponderant, ſed inclinatur ad maiorem
distantiam AC. ergo totum AD multò magis præponderabit,
quàm B. quod fieri non poteſt. poſita enim ſunt æ〈que〉ponde
rare. Quare AC maior eſſe non poteſt, quàm CB. ſed oſtenſa
eſt, ne〈que〉 ipſi CB æqualis eſſe: ac propterea minor eſt AC, quàm
CB. Manifestum eſt ita〈que〉 grauia ex distantiis inæqualibus æ〈que〉pon­
derantia, inæqualia eſſe; maiuſquè in minori diſtantia existere. quod
oportebat demonſtrare.
B
4 post hu­
ius.
1 poſt hu­
ius.
2 post hu­
ius.
SCHOLIVM.
In propoſitione verba illa, maius quidem ex minori, non haben
tur integra in codice græco, qui ſic habet, καὶ τό ἀπὸ το̄ν ἐλάσσονος
vbi deſiderari videtur μέιζον, vt integrè ita legatur, καὶ τὸ μείζον
ἀπὸ τοῡ ἐλάσσονος.
A
Sitquè maius A. Græcus codex, καὶ ἔσω τὸ α, vbi ſup­
plendum eſt, καὶ ἔσω μείζον τὸ α Hæc verò ita ſunt omnino reſti
tuenda, quia in vltima demonſtrationis concluſione inquit
Archimedes, Manifeſtum est ita〈que〉 grauia ex diſtantiis inæqualibus
æ〈que〉ponderantia inæqualia eſſe; maiuſquè in minori existere.
B
Poſtquam Archimedes duabus primis poſitionibus oſtendit, quno
ſe henant grauia ex diſtantijs ęqualibus in hac tertia conuertitſe ad
oſtendendum, quno ſe hennt ex diſtantijs inęqualibus. & quem in ſecundo
poſtulato aſsumpſit, quno ſe hennt grauia ęqualia in diſtantijs in ę­
qualibus conſtituta; nimirum quod eſt in longiori diſtantia, pręponde­
rat ei, quod eſt in breuiori. nunc oſtendit, quno inęqualia grauia ſe
hennt, ita vt ę〈que〉ponderent, in diſtantijs in ęqualibus poſita. demom
ſtratquè graue maius in breuiori diſtantia eem oportere, minus ve­
rò graue in longiori. & ecce quomodo Archimedes paulatim de
ducit nos in cognitionem principalis fundamenti, quod ſcilicet gra
ue ad graue eſt, vt diſtantia ad diſtantiam permutatim. Ex hoc. enim pri
mùm cognoſcimus grauius in minori, leuius autem in maiori
diſtantia eſſe debere, ſi ę〈que〉ponderare debent.
1
PROPOSITIO. IIII.
Si due magnitudines æquales non idem centrum
grauitatis habuerint, magnitudinis ex vtriſ〈que〉
magnitudinibus compoſitæ centrum grauitatis
erit medium rectæ lineæ grauitatis centra magni
tudinum coniungentis.
Sit quidem A

centrum grauita
tis magnitudi­
nis A. B uerò
ſit centrum gra­
uitatis magni­
tudinis B iun­
staquè AB bifariam diuidatur in C. dico magnitudinis ex utriſquè ma­
gnitudinibus compoſitæ centrum grauitatis eſſe punctum C. ſi. enim non; ſit
utrarumquè magnitudinum AB centrum grauitatis D, ſi fieri potest. Quòd
autem ſit in linea AB, præoſtenſum est. Quoniam igitur punstum D cem
trum eſt grauitatis magnitudinis ex AB compoſitæ, ſuſpenſo puncto D, magni
tudines AB æ〈que〉ponderabunt. magnitudines igitur AB ęquales æ〈que〉
ponderant ex diſtantiis AD DB in ęqualibus exiſtentibus; quod fie
ri non poteſt. æqualia. enim grauia ex diſtantiis in a qualibus non æ〈que〉ponde­
rant. non eſt igitur D ipſarum magnitudinum centrum grauitatis.. Qua
re manifestum est punstum C centrum eſſe grauitatis magnitudinis ex AB
compoſitæ. quod demonſtrare oportebat.
def. centri
grauit.
contra 2.
post huius
2 post hu­
ius.
25[Figure 25]
SCHOLIVM.
26[Figure 26]
Poſſunt magnitudines ęquales idem centrum
grauitatis habere, vt duo parallelogramma æ­
qualia ad rectos ſibi inuicem angulos exiſten
tia: triangulum quo〈que〉 & parallelogrammum in­
terſe æqualia. propterea cubos, piramides, cylin
dros, & huiuſmodi alias magnitudines ęqua
les idem grauitatis centrum herre intelligere poſſu
mus. propterea in propoſitione cùm inquit Archimedes
ſi duæ magnitudines æquales non idem centrum grauitatis
1habuerint. intelligendum eſt his verbis Archimedem ſuppo­
nere magnitudines ita eſſe conſtitutas, vt à centro ad centrum
duci poſſit recta linea. quod idem obſeruandum eſt in prima
propoſitione ſecundi libri huius.
Súmoperè aút animaduertenda ſunt nonnulla, quibus vtitur
Archimedes in hac propoſitione, cùm ſint communiſſima,
& maximè vtilia in hac ſcientia. ac primùm quidem conſide
randum occurrit, quid ſibi vult Archimedes per magnitudi
nem ex vtriſ〈que〉 magnitudinibus AB compoſitam. Nam ma­
gnitudines AB ſunt inuicem ſeparatę, & ſunt duę, ipſe autem
vtram〈que〉 vnam tantùm conſiderat. quod quidem ita intelli­
gendum eſt. quoniam ſcilicet recta linea AB eas coniungit; ideo
Archimedes conſiderat vnam tantùm eſſe magnitudinem; quę
conſtat ex ipſis AB, & efficitur vna magnitudo à linea AB.
cuius munus eſt non ſolùm connectere magnitudines AB,
ita vtne〈que〉 ad ſe ampliùs accedere, ne〈que〉 recedere inuicem
poſſint; ſintquè ab hac linea quaſi compulſę eundem ſemper
interſe ſeruare ſi tum: verum etiam ſi ſuſpendantur ex C, in­
telligendum eſt linea AB in rectitudinem iacere, inſuperquè
ſuſtinere magnitudines AB. Ne〈que〉 magis vna eſt magnitudo
quadrilaterum, pentagonum, cubus, & huiuſmodi aliæ, quàm
ſit magnitudo, quæ componitur ex magnitudinibus AB v­
nà cum linea AB. quòd ſi eſt vna tantùm magnitudo, ergo
vnum habet centrum grauitatis. Archimedes igitur quęrit cen
trum grauitatis huiuſce magnitudinis; demonſtratquè cen
trum eſſe in puncto C. quod eſt medium lineæ AB. notan
dum eſt autem Archimedem non conſiderare grauitatem li­
neę AB. vt potè, quę longitudo tantùm exiſtat. Quòd ſi quis
etiam mente concipere vellet lineam AB grauitate pręditam
eſſe; nihilominus centrum grauitatis lineę AB ſimiliter eſſet
in eius medio C. nam longitudo AC longitudini CB eſt
æqualis; ac propterea hę quidem longitudines eſſent inter ſeſe
ę〈que〉ponderantes. Quare, ſiue conſiderata grauitate lineę AB,
ſiue minùs, centrum grauitatis magnitudinis ex AB compo
ſitę eſt medium rectę lineę, quæ centra grauitatis magnitudinum
coniungit. Et hoc modo ſi plures etiam eſſent magnitudines
à recta linea coniunctę, eodem modo eas pro vna tantùm ma
1gnitudine ex pluribus magnitudinibus compoſita accipere po
terimus, veluti Archimedes in ſe〈que〉ntibus accipiet.
Argumentandi modus in eſt in hac demonſtratione maxi­
ma conſideratione dignus, & huius ſcientiæ maximè pro­
prius. cùm enim dixiſſet Archimedes poſito centro grauitatis
magnitudinis ex AB compoſitæ in puncto D, ſtatim infert.
Quoniam igitur punctum D centrum eſt grauitatis magnitudinis ex
AB compoſita, ſuſpenſo puncto D, magnitudines AB æ〈que〉pondera­
bunt. hoc eſt ſi magnitudo ex AB compoſita ſuſpendatur ex
D, manebit, vt reperitur; nec amplius in alteram partem in cli
nabit. quod euenit ob naturam centri grauitatis, quod talis
eſt naturæ (ſicuti initio explicauimus) ut ſi graue in eius cen­
tro grauitatis ſuſtineatur, eo modo manet, quo reperitur, dum
ſuſpenditur; parteſquè undiquè æ〈que〉ponderant. & ob id ſi
magnitudo ex AB compoſita ſuſpendatur in eius centro gra
uitatis, manet; parteſquè AB æ〈que〉ponderant. ac propterea
quando in ſe〈que〉ntibus quærit Archimedes, quoniam grauia
æ〈que〉ponderare debent, tunc tantùm quærit ipſorum centrum
grauitatis, ut in ſexta, ſeptimaquè propoſitione in quit Archi­
medes magnitudines ę〈que〉ponderare ex diſtantijs, quę permu
tatim proportionem habent, ut ipſarum grauitates, in demom
ſtratione tamen quærit, vbi nam eſt centrum grauitatis magni
tudinis ex vtrisquè compoſitę. quo inuento, ſtatim neceſſariò
ſequitur, magnitudines, ſi ex ipſo centro ſuſpendantur, æ〈que〉
ponderare.
Hinc colligere poſſumus alterum argumentandi modum,
conuerſo nempè modo, veluti in eadem figura, ſi dicamus
grauia AB ſuſpenſa ex C æ〈que〉ponderant, ſtatim inferre
poſſumus, punctum C ipſorum ſimul grauium, hoc eſt ma
gnitudinis ex ipſis AB compoſitę centrum eſſe grauitatis.
Quare ad ſe inuicem conuertuntur, hoc punctum eſt horum
grauium centrum grauitatis; ergo hęc grauia ex hoc puncto
æqùeponderant; & è conuerſo, nempè hæc grauia ex hoc pun
cto æ〈que〉ponderant, ergo idem punctum eſt ipſorum centrum
grauitatis. ſed ad uertendum hanc ſequi conuertibilitatem, quan­
do præfatum punctum eſt in recta linea, quæ centra grauita­
tum ponderum coniungit; deinde quando hęc linea non eſt
1horizonti perpendicularis. ſecus aurem minimè. Nam ſi pon
dera AB ſint in libra ADB, quę ſit arcuata, vel angulum con­
ſtituat, ſiue intelligatur libra recta linea AB, cui affixa ſit
perpendicularis CD. vt in tractatu de libra noſtrorum Me­
chanicorum diximus. ſuſpendantur autem pondera AB ex

D, & æ〈que〉ponderent; non
ſequitur tamen, ergo D
centrum eſt grauitatis ma­
gnitudinis ex AB com­
poſitę. centrum enim gra
uitatis in linea exiſtit AB
quæ centra grauitatis ma
gnitudinum AB coniun
git, nempe in C. Verùm coniungat recta linea AB centra

grauitatis æqualium ponderum AB, lineaquè
AB, cuius medium ſit C, in centrum mundi ten­
dat, magnitudoquè ex ipſis AB compoſita vbi­
cun〈que〉 ſuſpendatur in linea AB, vt in E; ma
nebunt vti〈que〉 pondera AB ex E ſuſpenſa, vt in
prima propoſitione de libra noſtrorum Mecha­
nicorum oſtendimus. cùm C ſit ipſorum centrum
grauitatis, & EC ſit horizonti erecta. Et quam­
uis magnitudo ex ipſis AB compoſita ex E ſu
ſpenſa maneat; non propterea ſequitur ergo E
centrum eſt grauitatis magnitudinis ex ipſis AB
compoſitę. niſi fortè accidat ſuſpenſio ex puncto
C. Præterea verò aduertendum eſt in hoc caſu pon
dera AB, dici quidem poſſe, manere, non autem
æ〈que〉ponderare. omnia nimirum, quę æ〈que〉ponderant, ma­
nent; ſed non è conuerſo, quæ manent, æ〈que〉ponderant. Nam
ſi pondus A maius fuerit pondere B; ſiue B maius, quàm
A, vbicun〈que〉 fiat ſuſpenſio in linea AB, ſemper ob eandem
cauſam, quomodocun〈que〉 ſint pondera, manebunt; non ta­
men æ〈que〉ponderabunt. Vt enim pondera æ〈que〉ponderent,
requiritur, vt pars parti, virtuſquè vnius virtuti alterius hinc
inde reſiſtere, & æquipollere poſſit; vt propriè dici poſſint pom
dera æ〈que〉ponderare. & vt hoc euenire poſſit, oportet, vt
1tes ex determinatis diſtantijs determinatas quo〈que〉 habeant
grauitates; ſi ex dato puncto æ〈que〉ponderare debent. Quòd
ſi in hoc caſu datum fuerit punctum C, ex quo pondera AB
ex æqualibus diſtantijs CA CB ę〈que〉ponderare debeant: o­
porteret, vt pondera AB (ex demonſtratis) ſemper eſſent æ­
qualia. Quoniam autem quomodocun〈que〉 ſint pondera, hoc eſt; ſi
ue pondus A maius, ſiue minus fuerit, quàm B, manent, ſi
igitur dixerimus, ergo pondus A ponderi B ę〈que〉ponderat;
eſſet omnino inconueniens. cùm ex ijsdem diſtantijs eidem pom
deri pondus quandoquè maius, quandoquè minus ę〈que〉pon­
derare non poſſit; vt in hoc caſu accidere poteſt. Quocirca
nec propriè dici poſſunt pondera, ſiue in libra AB, ſiue ex
diſtantijs CA CB conſtituta eſſe. Vndè ne〈que〉 Archimedis
propoſitiones in hoc caſu ſunt intelligendę quandoquidem
in his propriè quærit ponderum, magnitudinumquè æ〈que〉­
ponderationes. ne〈que〉 enim in hac quarta demonſtratione in
hoc caſu potuiſſet Archimedes abſurdum oſtendere, ſi C non
eſt grauitatis centrum magnitudinis ex AB compoſitæ, ſit
E. facta igitur ex E ſuſpenſione, magnitudines æquales AB
ex in æqualibus diſtantijs EA EB ę〈que〉ponderabunt. quod
fieri non poteſt. non enim hoc eſt abſurdum; cùm pondera
ex E ſuſpenſa maneant idcirco quando linea AB eſt horizom
ti erecta; propriè ad rem noſtram minimè pertinet. Ex dictis
igitur ſemper valet conſe〈que〉ntia, hoc punctum horum pon
derum centrum eſt grauitatis, ergo ſi ex hoc ſuſpendantur, pom
dera ę〈que〉ponderant. non autem è conuerſo. niſi quando ar­
gumentatio ſumitur ſemper ex recta linea, quæ centra graui
tatis magnitudinum coniungit, & quando hęc linea non eſt

horizonti erecta. hac enim
ratione quocun〈que〉 modo
recta linea ſe habeat, ſem­
per ſequitur idem. Vt ſi li­
nea AB fuerit, ſiue non fue­
rit horizonti æquidiſtans,
ipſius medium C centrum
erit grauitatis magnitudi­
nis ex magnitudinibus AB æqualibus compoſitę. vnde ſequi
1tur, ſi appendantur pondera AB ex C, æ〈que〉ponderare. &
è conuerſo, ſi AB pondera ex C æ〈que〉ponderant, ergo C
centrum grauitatis exiſtit. ex quibus ſequitur lineam AB, pom
deraquè manere eo modo, quo reperiuntur. vt in noſtro me­
chanicorum libro in codem tractatu de libra demonſtraui­
mus, & aduerſus illos, qui aliter ſentiunt, abundè diſpu­
tauimus.
poſt quar­
tam propo
ſitionem.
*
27[Figure 27] 28[Figure 28] 29[Figure 29]
In demonſtratione autem huius quartæ propoſitionis in­
quit Archimedes. Quòd autem ſit in linea AB, præostenſum eſt. qua
ſi dicat Archimedes, ſe priùs oſtendiſſe centrum grauitatis ma
gnitudinis ex AB compoſitæ eſſe in linea AB; quod tamen
in ijs, quæ dicta ſunt, non videtur expreſſum. virtute tamen ſi
conſideremus ea, quę in prima, tertiaquè propoſitione dicta
ſunt, facilè ex his concludi poteſt, centrum grauitatis magni­
tudinis ex duabus magnitudinibus compoſitæ eſſe in recta li
nea, quæ ipſarum centra grauitatis coniungit. Quare memi­
niſſe oportet eorum, quę a nobis in expoſitione primi poſtu
lati huius dicta fuere, nempè Archimedem ſupponere, diſtan­
tias eſſe in vna, eademquè recta linea conſtitutas. ideoquè in
prima propoſitio nec inquit, Grauia, quę ex diſtantijs ęquali
bus æ〈que〉ponderant, æqualia eſſe inter ſe; Archimedes què demom
ſtrat, quòd quando æ〈que〉ponderant, ſunt æqualia: ex dictis
ſequitur, ſi æ〈que〉ponderant, ergo centrum grauitatis magni­
tudinis ex ipſis compoſitę erit in eo puncto, vbi æ〈que〉ponde­
rant; hoc eſt in medio diſtantiarum, lineę ſcilicet, quę grauium
centra grauitatis coniungit. quod idem eſt, ac ſi Archimedes
dixiſſet. Grauia, quę habent centrum grauitatis in medio li­
neę, quę magnitudinum centra grauitatis coniungit, ęqua­
lia ſunt inter ſe. cuius quidem hęc quarta propoſitio videtur
eſſe conuerſa. quamuis Archimedes loco grauium nominet
magnitudines. Pręterea in tertia propoſitione, quoniam oſten­
dit Archimedes, inęqualia grauia ę〈que〉ponderare ex diſtantijs
inęqualibus, ita vt grauius ſit in minori diſtantia, ſequitur er
go centrum grauitatis eſt in eo puncto, vbi æ〈que〉ponderant;
& idem eſt, ac ſi dixiſſet, in æqualium grauium centrum gra­
uitatis eſt in recta linea, quæ ipſorum centra grauitatis con­
iungit; ita vt ſit propinquius grauiori, remotius uerò leuiori.
1vnde ſequitur centrum grauitatis ipſorum grauium ubicum
〈que〉 eſſe poſſe in recta linea, quę ipſorum centra grauitatis con
iungit. Ex quibus concludi poteſt, centrum grauitatis magni­
tudinis ex duabus magnitudinibus compoſitę eſſe in recta li
nea, quæ ipſorum centra grauitatis connectit.
Poſtremò notandum eſt, Archimedem ea, quæ in ſuperio
ribus propoſitionibus nuncupauit grauia, in hac quarta pro
poſitione, veluti etiam in ſe〈que〉ntibus, non ampliùs grauia,
ſed (vti diximus) magnitudines nominare. quod quidem his
de cauſis id ab ipſo factum exiſtimo. primùm enim, quia in
his expreſse quærit centrum grauitatis; quod quidem centrum,
quamuis ſit centrum grauitatis, potiùs reſpicit magnitudinem,
quàm graue aliquod. Nam cùm dicimus centrum grauitatis,
ſtatim innuimus ſitum, ſitum inquàm determinatum figu­
ræ, in qua eſt; ſiquidem centrum grauitatis eſt punctum, &
(vt ita dicam) punctum grauitatis eius, in quo eſt. & ideo,
quoniam magnitudo formam habet dete mina tam, centrum
grauitatis rectè poteſt reſpicere ſitum reſpectu magnitudinis,
in qua eſt; quod tamen efficere non poteſt reſpectu grauis.
etenim graue, ut graue eſt, non habet formam determina tam;
cùm eadem grauitas eſſe poſſit in cubo, in piramide, aliiſquè
corporibus quibuſcun〈que〉, modò minoribus, modò maiori­
bus, pro ut ſunt diuerſarum ſpecierum. quare centrum grauita
tis non poteſt reſpicere ſitum in grauibus, quatenus grauia con
ſiderantur; ſed quatenus magnitudines exiſtunt. Præterea Ar­
chimedes loco grauium magnitudines nominat, quia eas di­
uiſibiles conſiderat, quod eſt proprium magnitudinis; vt in ſe
xta, ſeptima, & octaua propoſitione. & quamuis, dum diuidum
tur magnitudines, grauia quo〈que〉 diuiſa proueniant; non ta­
men propterea grauia diuiduntur, ut grauia. non.n. hoc ipſis
competit, vt grauibus; ſed vt magnitudinibus, quæ ſunt per
ſe diuiſibiles. Archimedes igitur his de cauſis nomen grauium
in magnitudines mutauit. in ſuperioribus enim theoremati­
bus pertractauit, quomodo res æ〈que〉ponderant ex diſtantijs
modò æqualibus, modò in æqualibus. & quoniam res ę〈que〉pon
derant, pro ut ſunt magis grauia, & minùs grauia; non ut sunt
maiores, vel minores magnitudines, ſiquidem talis naturæ
1eſſe poteſt minor magnitudo, quę maiore magnitudine alte
rius nature grauior exiſtat; proindé Archimedes in ſuperiori­
bus rectè grauia nuncupauit; optimèquè in his magnitudines
vocat. At verò aduertendum eſt, quòd quamuis Archimedes
in his magnitudines nominet, non propterea exiſtimandum
eſt, eum intelligere magnitudines tantùm; ſed magnitudines
grauitate pręditas, ita ut in ipſis omnino grauitatem reſpiciat.
Etenim pluribus modis intelligere poſſumus magnitudines,
vel enim ut ſint inter ſe eiuſdem ſpeciei, vel diuerſæ; nec non
inſuper homogeneæ, vel heterogeneæ. vt in hac propoſitione
quando Archimedes proponit duas magnitudines ęquales, tuc
intelligere poſſumus eas eſſe eiuſdem ſpeciei, & homogeneas;
quæ, cùm ſint æquales, erit & grauitas vnius grauitati alterius
æqualis. ſi verò conſideremus eas eſſe diuerſæ ſpeciei, & e­
tiam heterogeneas; tunc quando Archimedes proponit has
magnitudines æquales; intelligendum eſt, eas eſſe æquales in
grauitate; quæ quidem efficit, vt demonſtratio, quod propo­
ſitum eſt, concludat. vt ex eius demonſtratione patet. Et his
quo〈que〉 modis intelligere poſſumus magnitudines in ſe〈que〉n
tibus vſ〈que〉 ad nonam propoſitionem in quibus ſcilicet intel
ligere poſſumus magnitudines eſſe non ſolùm eiuſdem ſpe­
ciei, vel diuerſæ, verùm etiam & homogeneas. & heteroge­
neas. ut poſt ſeptimam clariùs oſtendemus. Verùm de­
monſtrationes clariores redduntur, ſi intelligamus magnitu­
dines eſſe eiuſdem ſpeciei, & homogeneas, in quibus graui­
tas magnitudini reſpondet, vt ſi ipſarum altera fuerit alte­
rius dupla, & grauitas vnius grauitatis alterius dupla exiſtat.
Quòd ſi magnitudo fuerit alterius tripla, vel quadrupla, &c.
erit & grauitas grauitatis tripla, vel quadrupla, & ſic dein­
ceps. deinde ſi magnitudo bifariam diuiſa fuerit, & ipſius gra
uitas in duas ęquas partes ſit quo〈que〉 diuiſa. quòd ſi magnitu­
do in plures diuidatur partes, & grauitas quo〈que〉 in totidem
eiuſdem proportionis diuiſa proueniat.
1
PROPOSITIO. V.
Si trium magnitudinum centra grauitatis in re
cta linea fuerint poſita, & magnitudines æqualem
habuerint grauitatem, acrectæ lineæ inter centra
fuerint æquales, magnitudinis ex omnibus magni
tudinibus compoſitæ centrum grauitatis erit pum
ctum, quod & ipſarum mediæ centrum grauitatis
exiſtit.
30[Figure 30]
Sint tres magnitudines ACB. ipſarum autem centra grauitatis ſint
puncta ACB in resta linea ACB poſita. ſint verò magnitudines ACB
æquales; rectæquè lineæ AC CB inter centra ipſarum aquales. Di
co magnitudinis ex omnibus ACB magnitudinibus compoſitæ centrungra
uitatis eſſe punctum C. quod eſt centrum grauitatis mediæ ma­
gnitudinis. Quoniam enim magnitudines AB æqualem habent graui
tatem; magnitudinis ex vtriſ〈que〉 AB compoſitæ centrum graui
tatis erit punctum C: cùm ſint AC CB æquales. ſitquè propterea
punctum C medium rectæ lineę AB. Sed & magnitudinis C cem
trum grauitatis est idem punctum C. punctum ergo C trium ma­
gnitudinum ABC centrum quo〈que〉 grauitatis erit. Quare pa
tet magnitudinis ex omnibus magnitudinibus ACB compoſitæ centrum
grauitatis eſſe punctum, quod & magnitudinis mediæ centrum graui­
tatis existit. quod demonſtrare oportebat.
1
4 huius.
COROLLARIVM. I.
Ex hoc autem manifeſtum eſt, ſi quotcunquè
magnitudinum, & numero imparium, gra­
uitatis in recta linea conſtituta fuerint; & magni­
tudines æqualem habuerint grauitatem; rectæquè
lineæ inter ipſarum centra fuerint æquales, ma­
gnitudinis ex omnibus magnitudinibus compoſi
tæ centrum grauitatis eſſe punctum, quod & ipſa­
rum mediæ centrum grauitatis exiſtit.
*
SCHOLIVM.
31[Figure 31]
Ex demonſtratione colligit Archimedes ſi plures fuerint
magnitudines, quam tres; dummodo ſint numero impares, vt
ABCDE; quarum centra grauitatis ABCDE reperiantur in li
nea recta AE. fuerint autem hę magnitudines æquales in gra
uitate. inſuper rectę lineę AB BC CD DE, quę ſunt inter cen­
tra grauitatis, fuerint æquales: magnitudinis ex omnibus ma
gnitudinibus ABCDE compoſitæ centrum grauitatis eſſe
punctum C. quod eſt centrum grauitatis magnitudinis
mediæ.
Eodem enim modo, ac primùm quidem ex demonſtratio
ne patet punctum C centrum eſſe grauitatis trium magnitudinum
BCD, & quoniam AB BC ſunt æquales ipſis CD DE,
1erit AC ipſi CE ęqualis. cùm què ſit grauitas magnitudinis
A ęqualis grauitati ipſius E, erit itidem punctum C magni
tudinum AE centrum grauitatis. ergo punctum C magni
tudinis ex omnibus magnitudinibus ABCDE compoſitæ
centrum grauitatis exiſtit.
4 huius.
Quòd ſi fuerint ad huc plures magnitudines, impares verò
extiterint; quæ ita ſe habeant, vt expoſitum eſt; ſimiliter oſtem
detur, centrum grauitatis mediæ magnitudinis centrum eſſe
grauitatis magnitudinis ex omnibus magnitudinibus com­
poſitæ.
In hoc corollario, verba illa, & magnitudines æqualem habue­
rint grauitatem in greco codice ita habentur. εἵκα τατε ἴσον ἀπέχον­
τα ἀπὸ τοῦ μέσου μεγέθεος ἴσον βάρος ἔχωντι quorum multa ſuperuaca­
nea nobis viſa ſunt; loco quorum (vt arbitror) rectè congruent
καὶ τὰ μεγέθεα ἴσον βάρος ἔχωντι, vt vertimus. Nam ſi ordinis at〈que〉
conditionum propoſitę propoſitionis ratio habenda eſt, opor
tet vt magnitudines ęqualem habeant grauitatem; Nam &
Archimedes in ſe〈que〉ntibus demonſtrationibus ijs vtitur, ut
ſunt æ〈que〉graues. Adhuc tamen veritatem habebit ſi cæteris
conditionibus illud quo〈que〉 addere voluerimus, nempe ſi ma
gnitudines à media magnitudine æqualiter diſtantes æqualem habuerint
grauitatem eodem modo punctum C centrum erit grauitatis

magnitudinis ex omnibus ABCDE compoſitę, Nam ſi ma­
gnitudines à media magnitudine ſunt ę〈que〉graues; ęqualem
quo〈que〉 habebunt grauitatem magnitudines AE; veluti ma­
gnitudines BD, quæ æqualiter à media magnitudine C di­
ſtant. & quam uis non ſint omnes æ〈que〉graues, ſufficit, vt AE
quæ ęqualiter à media magnitudine diſtant, ſint ę〈que〉graues.
ſimiliter BD ę〈que〉graues. Eadem enim ratione, quoniam
BD ſunt æ〈que〉graues, & diſtantiæ BC CD ęquales; erit C
1rum BD centrum grauitatis. pari què ratione C erit centrum
grauitatis magnitudinum AE ę〈que〉grauium. cum ſint AC
CE ęquales, & idem C eſt grauitatis centrum magnitudinis
C. ergo punctum C magnitudinis ex omnibus magnitudini­
bus ABCDE compoſitę centrum grauitatis exiſtit.
*
32[Figure 32]
COROLLARIVM. II.
Si verò magnitudines fuerint numero pares;
& ipſarum centra grauitatis in recta linea extite­
rint, magnitudineſquè æqualem habuerint
tatem, rectæ què lineæ inter centra fuerint æqua
les: magnitudinis ex omnibus magnitudinibus com
poſitæ centrum grauitatis erit medium rectæ li­
neæ, quæ magnitudinum centra grauitatis coniun­
git. vt in ſubiecta figura.
*
33[Figure 33]
SCHOLIVM.
Colligit præterea Archimedes ſi magnitudines ABCDEF
fuerint numero pares, quarum centra grauitatis ABCDEF in
recta linea AF ſint conſtituta; magnitudineſquè ſint æquales
in grauitate; ſintquè inter centra lineę AB BC CD DE EF
æ quales. diuidatur autem AF bifariam in G. erit punctum
G centrum grauitatis magnitudinis ex omnibus compoſi­
tæ quod quidem, figura tantùm inſpecta, perſpicuum eſt.
Cùm enim magnitudines AF ſint æ〈que〉graues, & AG GF
1 ſint æquales, erit G centrum grauitatis magnitudinis ex AF
compoſitæ. quia verò AB eſt ipſi EF æqualis, reliqua BG
ipſi GE æqualis exiſtet. & ſunt magnitudines BE ę〈que〉gra­
ues, erit idem G centrum grauitatis magnitudinum BE. ſimili­
ter cùm ſit BC æqualis DE, relin〈que〉tur CG ipſi GD ęqua­
lis; magnitudinesquè CD ſunt ę〈que〉graues. ergo punctum G cem
trum eſt quo〈que〉 magnitudinum CD. Vnde ſequitur, punctum
G magnitudinis ex omnibus magnitudinibus ABCDEF con­
poſitæ centrum grauitatis exiſtere.
4 huius.
Hoc quo〈que〉 loco verba illa magnitudineſquè æqualem habuerint
grauitatem. Græcus codex ita mendosè legit. καὶ τὰ μέσα αὔτης ἴσον
βάρος ἔχωντι, quæ quidem verba hoc modo reſtitui poſſunt.
καὶ τὰ μεγέθεα ἴσον βάρος ἔχωντι.
*
In præcedenti propoſitione oſtendit Archimedes, quomo
do ſe habet centrum grauitatis magnitudinis ex duabus ma­
gnitudinibus ęqualibus compoſitæ. In hac autem demonſtrat,
vbi ſimiliter grauitatis centrum reperitur inter plures magni­
tudines æ〈que〉graues, & inter ſe ęqualiter diſtantes. ex quibus
tandem colliget fundamentum ſæpiùs dictum. nempè ſi ma­
gnitudines ę〈que〉ponderare debent; ita ſe habebit magnitudi­
num grauitas ad grauitatem, ut ſe habent diſtantiæ permuta
tim, ex quibus ſuſpenduntur. & hoc demonſtrat Archimedes
in duabus ſe〈que〉ntibus propoſitionibus. nam magnitudines,
vel ſunt commenſurabiles interſeſe, vel incommenſurabiles.
de commenſurabilibus aget in ſe〈que〉nti: de incommenſurabi
libus verò in ſeptima propoſitione. & Archimedes duas ſe〈que〉n­
tes propoſitiones ueluti coniunctas proponit. Nam in ſexta
inquit Magnitudines commenſurabiles, &c. in ſeptima uerò in­
quit, Si autem magnitudines ſuerint incommenſurabiles, quaſi vna tam
tùm ſit propoſitio in duas partes diuiſa. ita ut ne〈que〉 numeris
eſſent diſtinguende, ſed pro vna tantùm propoſitione ſummen
dæ, obſe〈que〉ntis autem demonſtrationis faciliorem intelligen
tiam hęc priùs præmittimus.
LEMMA.
Si duę fuerint magnitudines in æquales, quarum maior ſit
alterius dupla, tertia verò quędam magnitudo minorem
1tiatur. maiorem quo〈que〉 in partes numero pares metietur.
Sint duę in ęquales magni

tudines AB, ſitquè A ipſius
B duplex. magnitudo autem
C magnitudinem B metia­
tur. Dico C magnitudinem
A metiri, menſurationesquè numero pares eſſe. Quoniam
enim C metitur B, eodem numero C metietur medietates
ipſius A, quæ ſuntipſi B æquales. ergo duplo plures erunt nu
mero menſurationes ipſius A, quàm ipſius B. quare menſu­
rationes ipſius A ſunt numero pares. duplum enim ſemper
paritatem ſecum affert. quod demonſtrare oportebat.
34[Figure 34]
Porrò maxima in his duabus ſe〈que〉ntibus propoſitionibus
adhibenda eſt diligentia; quibus tota rerum Mechanicarum
ratio in nititur. Quocirca vt harum propoſitionum demon­
ſtrationes perfectè intelligere poſſimus; præter eos argumen­
tandi modos, quorum ante quintam huius propoſitionem
meminimus; alterum quo〈que〉 modum, quo Archimedes in

hac ſexta propoſitione vtitur, nouiſſe oportet. vt ſcilicet, ſi ma
gnitudo A æ〈que〉ponderatipſis BC facta ſuſpenſione ex pun­
cto D; ita ſcilicet, vt D ſit centrum grauitatis magnitudinis
ex omnibus ABC magnitudinibus compoſitæ; ipſarum verò
1magnitudinum BC, hoc eſt magnitudinis ex BC compoſi­
tæ centrum grauitatis ſit punctum E; auferantur verò BC
à linea EA, & ipſarum loco ponatur in E magnitudo;
quæ ſit vtriſ〈que〉 ſimul BC ęqualis, vt in ſecunda figura. Dico
eodem modo pondera ABC ę〈que〉ponderare in prima figu­
ra, veluti grauia AE in ſecunda.
35[Figure 35]
Primum autem, vthoc recte per

pendamus, intelligantur pondera
BC (vt in tertia figura) ſeorſum
à linea CA, & penes diſtantias EC
EB conſtituta. quorum quidem pon­
derum ſit centrum grauitatis E. ſi igitur intelligatur poten
tia in E ſuſtinere pondera BC, hoc eſt pondus exipſis BC
compoſitum: pondera uti〈que〉 manebunt. quòd ſi ambo pe­
penderint, vt quinquaginta, potentia in E tantùm quinqua
ginta ſuſtinebit. quoniam totum ſuſtinebit pondus ex ipſis
compoſitum, auferantur verò pondera BC à ſitu BC, intelli
ganturquè pondera eſſe in E conſtituta; hoc eſt vnum ſit
pondus ex ipſis ſimul iunctis compoſitum, cuius centrum gra­
uitatis ſit in E conſtitutum; tunc eadem potentia in E eo­
dem modo hoc pondus ſuſtinebit; propterea quod eodem mo­
do quinquaginta tantùm ſuſtinebit. Quare pondera BC tam
ex diſtantijs EC EB grauitant, quàm ſi vtra〈que〉 in E con
ſtituta fuerint; vel quod idem eſt, quàm pondus ipſis BC ſi­
mul æquale in E poſitum. Ex quo patetid, quod initio prę­
fati ſum us, nempe, vnumquodquè graue in eius centro gra­
uitatis propriè grauitare. Quocum 〈que〉 enim modo eadem gra
uia ſeſe habent, eodem ſemper modo in eius grauitatis centro
grauitant.
per def.
cent. grau.
36[Figure 36]
Quibus cognitis, intelligantur nunc grauia BC in linea
CA poſita eſſe; ut in ſuperiori figura: & ut quod propoſitum
fuit, oſtendatur; hoc modo argumentari licebit. Quoniam
enim magnitudines BC ſuam habent grauitatem in E, ſiqui
dem pro vna tantùm intelliguntur magnitudine ex BC com
poſita, cuius punctum E centrum grauitatis exiſtit. in ſecum
da verò figura magnitudo E ſimiliter ſuam habet grauitatem
in puncto E; quod eſt eius centrum grauitatis. at〈que〉
1do E eſtipſis BC ſimul ſumptis ęqualis. diſtantię verò AD
DE ſunt æquales, cum ſint ęedem; erit vti〈que〉 punctum D in
ſecunda figura centrum grauitatis magnitudinis ex AE com­
poſitæ, veluti D in prima figura ipſarum ABC centrum gra
uitatis exiſtit. ac propterea in vtra〈que〉 figura pondera æ〈que〉­
ponderabunt:
Cæterum hoc quo〈que〉 oſtendemus hoc pacto.
37[Figure 37]
Iiſdem nam〈que〉 poſitis; æ〈que〉ponderarent ſcilicet grauia
ABC facta ex D ſuſpenſione. ſitquè punctum E
centrum grauitatis ponderum CB. quæ quidem pondera
CB grauitatis centrum habeant in linea CB. Dico pondus
A ponderi ipſis CB ſimul ſumptis æquali in E conſti­
tuto æ〈que〉ponderare. Mente concipiamus diſtantias EC
EB, manente centro E, circa ipſum circumuerti poſſe;
vt modò ſint in FEG, modò in HEK. ſimiliter in­
telligantur pondera CB, modò in FG, modò in HK
exiſtere. Quoniam igitur punctum E. centrum eſt
grauitatis ponderum CB; erit idem E (cùm ſitum
nonmutet) centrum grauitatis ponderum in ſitu FG, ac
ponderum in HK exiſtentium. Quiaverò vnumquod­
〈que〉 pondus (ex dictis) propiè in eius centro grauitatis graui
tat; pondera ſimul CB ſiue ſint in FG, ſiue in HK, proprie
in puncto E grauitabunt. At verò quoniam idem
1pondus vnam & eandem ſemper habet grauitatem; erit pondus
ex CB compoſitum æ〈que〉graue, tam in ſitu CB, quàm in
FG, & in ſitu HK. conſiderando nempe pondera CB (ut
revera ſunt) nilaliud eſſe niſi vnum tantùm pondus ex CB
compoſitum. Ex quibus perſpicuum eſt, punctum E eodem
ſemper modo grauitare. Quare quoniam pondera CB in ſi­
tu CB ipſi A ę〈que〉ponderant, ſuamquè habent grauitatem
in puncto E; eadem pondera CB ſiue ſint in FG, ſiue in
HK, eidem ponderi A æ〈que〉ponderabunt. ſiquidem propriè
ſemper grauitant in E, & eandem ſemper habent grauita­
tem Intelligatur deni〈que〉 HEK in centrum mundi tendere; e­
runtvti〈que〉 vtra〈que〉 pondera HK, tanquam in puncto E com
ſtituta, vt ex prima propoſitione noſtrorum Mechanicorum
elici poteſt, quamuis perſe notum ſit. ſiquidem ſeorſum pon
dus H ſecundùm eius centrum grauitatis propriè grauitat ſu
per puncto E; pondus verò K eſt, tanquam ex E appenſum;
vndè & in eodem puncto E quo〈que〉 grauitat. Ita〈que〉 quoniam
ambo propriè grauitant in E, erunt pondera HK perinde,
acſi vnum eſſet pondusipſis HK, hoc eſtipſis CB æquale, cu
ius centrum grauitatis ſit in E conſtitutum. atverò pondus
A ipſis CB in ſitu HK exiſtentibus æ〈que〉ponderat. ergo idem
pondus A ipſis CB in E conſtitutis, hoc eſt ponderi ipſis CB
ſimul ſumptis ęquali in E poſito æ〈que〉ponderabit. quod de­
monſtrare oportebat.
Quod idem quo〈que〉, ſi plura eſſent pondera, ſimiliter o­
ſtendetur.
Valetita〈que〉 conſe〈que〉ntia, punctum D centrum eſtgra­
uitatis magnitudinis ex ponderibus ABC compoſitę; ergoi­
dem punctum D centrum eſt grauitatis ponderis in A, & pom
derisipſis BC ſimul ęqualis in E conſtituti. ex quo conſequi­
tur, quòd ſi magnitudines ABC ex D æ〈que〉ponderant, ergo
ex eodem D magnitudo ipſis BC ſimul æqualis in E poſita,
& magnitudo A æ〈que〉ponderabunt. quòd ſi rectè perpenda­
mus, nil aliud ſunt pondera in BC, niſi magnitudo in E con­
ſtituta. ſiquidem punctum E ipſius centrum grauitatis
exiſtit
In noſtro autem Mechanicorum libro in quinta
1tione tractatus de libra duas attulimus demon ſtrationes oſten­
tes duo pondera vt CB tam in punctis CB ponderare, quàm ſi
vtra〈que〉 ex puncto E ſuſpendantur. At verò quo niam demon
ſtrationes ibi allatæ ijs indigent, quę Archimedes in ſe〈que〉n­
ti ſexta propoſitione demonſtrauit, idcirco demonſtrationes
illæ huic loco non ſunt oportunæ; vt ex ipſisſumi poſſit tan­
quam demonſtratum pondera CB, tam in punctis CB pon­
derare, quàm ſi vtra〈que〉 ex E ſuſpendantur. Quare hoc loco hę
tantùm ſufficiant rationes, quæ dictæ ſunt. Ex quibus poteſt
Archime des diſtam conſe〈que〉ntiam colligere; nempè magni­
tudines ABC ex D æ〈que〉ponderant, auferantur autem BC,
& loco ipſarum vtriſ〈que〉 ſimul ę〈que〉grauis ponatur magnitu­
do in E; ſimiliter hęc magnitudo ipſi A æ〈que〉ponderabit. Po­
ſtea verò ex ijs, quæ Archimedes demonſtrauit, fieri poteſt re
greſſus; vapertiùs, manifeſtiùſ què cognoſcere valeamus, pon
dera BC ita ponderare, ac ſi vtra〈que〉 ex puncto E ſuſpen­
dantur.
38[Figure 38]
Cęterum hoc loco Archimedes non ſolùm de duobus, verum
etiam de pluribus ponderibus idipſum intelligendum admittit.
vt ſi magnitudines STVXZM æ〈que〉ponderent facta ſuſpenſio
ne ex puncto C. ſitquè magnitudinum MZ centrum grauitatis
D; ipſarum verò STVX ſit centrum grauitatis E. ſi ita〈que〉 ma
gnitudines STVX, & ZM ex C æ〈que〉ponderant; auferantur
STVX, quarum loco ponatur in E magnitudo ipſis STVX ſi
mul ſumptis ęqualis: auferanturquè ZM, at〈que〉 ipſarum loco po
natur in D magnitudo ipſis ZM ſimul ęqualis; tunclicetinfer
re, ergo hæ magnitudines in ED poſitæ ę〈que〉pondera­
bunt. Quod quidem ijsdem prorſus modis oſtendentur.
præſertim ſi mente concipiamus diſtantias ES EX,
1nec non magnitudines STVX in ſuis diſtantijs circa centrum
grauitatis E circumuerti poſſe; veluti diſtantias DZ DM, ma
gnitudineſquè ZM circacentrum D. moueantur autem
SEX, & ZDM, donec in centrum mundi vergant. ſimiliter
oſtendetur magnitudines STVX eſſe, ac ſi in E eſſent appen
ſę, ſiue conſtitutę; magnitudines verò ZM ac ſi in D poſi­
tæ fuerint. &c. Ex quibus ſequitur, ſi punctum C centrum
eſt grauitatis magnitudinum STVXZM. ponatur magnitu­
do ipſis STVX ſimul ſumptis ęqualis in E; magnitudo au
tem ipſis ZM ſimul æqualis in D; punctum C ſimiliter
ipſarum quo〈que〉 centrum grauitatis exiſtet. vnde vtro〈que〉 mo
do æ〈que〉ponderabunt. & ita in alijs, ſi plures fuerint magni­
tudines.
PROPOSITIO. VI.
Magnitudines commenſurabiles ex diſtantijs
eandem permutatim proportionem habentibus,
vt grauitates, æ〈que〉ponderant.
Commenſurabiles ſint magnitudines AB quarum centra grauita­
tis AB, & quædam ſit diſtantia E D, & vt ſe habet grauitas ma­
gnitudinis A ad grauitatem magnitudinis B, ua ſit diſtantia
DC ad distantiam CE. ostendendum eſi, ſi centra grauitatis AB fue
rint in punctis ED conſtituta, hoc eſt A in E, & B in D;
magnitudinis ex vtriſquè magnitudinibus AB compoſitæ centrum
grauitatis eſſe punctum C. Quoniam enim ita est magnitudo A ad
magnitudinem B, vt DC ad CE. eſt autem magnitudo A ipſi
B commenſurabilis; erit & CD ipſi CE commenſurabilis; hoc eſt
recta linea rectæ lineæ commenſurabilis exiſtet. Quare ipſarum EC
CD communis reperitur menſura. quæ quidem ſit N. deinde ponatur
ipſi EC æqualis vtra〈que〉 DG DK; ipſi verò DC æqualis EL. &
quoniam æqualis est DG ipſi CE, communi addita CG, erit DC
ipſi EG æqualis; ſed DC eſt ipſi EL ęqualis: erit igitur LE æqua­
lis ipſi EG. quare vtra〈que〉 LE EG ęqualis eſt ipſi DC. ac propte
1rea dupla est LG ipſius DC. quia verò vtra〈que〉 DG DK æqualis
facta eſt ipſi CE, erit & ipſa quo〈que〉 GK ipſius CE dupla. Quare
N vtran〈que〉 LG Gk metitur, cùm & ipſarum medietates DC CE

metiatur. Et quoniam magnitudo A ita eſt ad magnitudinem
B, vt DC ad CE, ut autem DC ad CE, ita eſt LG ad GK, utra〈que〉
enim vtriuſ〈que〉 duplex exiſtit (ſiquidem LG dupla eſt ipſius DC,
& GK itidem ipſius CE duplex) erit magnitudo A ad magni­
tudinem B, ut LG ad Gk; & conuertendo magnitudo B ad
magnitudinem A, vt KG ad GL. Quotuplex autem est LG ipſius
N, totuplex ſit magnitudo A ipſius F, erit vti〈que〉 LG ad N, vt
magnitudo A ad F, atqui est KG ad LG, vt magnitudo B ad
magnitudinem A: LG verò ad N eſt, vt magnitudo A i­
psam F, ex æquali igitur erit KG ad N, vt magnitudo B ad F quare æ­
〈que〉multiplex eſt kG ipſius N, veluti magnitudo B ipſius F. demon
ſtratum aunt eſt magnitudinem A ipſius F multiplicem eſſe, ſiquidem eſt
magnitudo A ad ipſam F, vt LG ad N, quæ quidem LG mul
tiplex eſt ipſius N. qua propter F ipſarum AB communis existit men
ſura. Jta〈que〉 diuiſa LG in partes LH, HE, EC, CG, ipſi N aquales,
cadent vti〈que〉 diuiſiones in punctis EC, quoniam Nipsam
metitur, nec non ipſam quo〈que〉 LE metitur; cùm ſit LE ipſi
CD æqualis. eruntquè diuiſiones LH, HE, EC, CG, numero
pares; cùm N dimidiam ipſius LG, hoc eſt CD metiatur.
1Averò ſimiliter diuiſa in partes OP QR ipſi F æquales; ſectio­
nes LH, HE, EC, CG in LG existentes magnitudini N æqua­
les, erunt numero æquales ſectionibus OPQR in magnitudine A
existentibus ipſi F æqualibus. Diuidantur ſectiones LH, HE, EC,

CG bifariam in punctis STVX. ſi it a〈que〉 in vnaqua〈que〉 ſestio
ne ipſius LG apponatur magnitudo æqualis ipſi F, quæ centrum gra­
uitatis babeat in medio ſectionis; vt ſi in LH ponatur magnitudo
S, in HE magnitudo T, in EC magnitudo V, & in
CG magnitudo X; ipſarum què vna quæ〈que〉 STVX ſit ipſi
F æqualis: habeat verò magnitudo S ſuum grauitatis centrum,
quod ſit punctum S, in medio ſectionis LH, nempè in pun­
cto S; ſimiliter cæteræ magnitudines TVX habeant cerrra
grauitatis; quæ ſint puncta TVX, in medio ſectionum HE,
EC, CG, in punctis nempè TVX, erunt centra grauitatisma
gnitudinum STVX in recta linea conſtituta, & quomao
SH dimidia eſt ipſius LH, veluti HT ipſius HE, erit ST,
ipſius LE dimidia, vnaquæ〈que〉 verò LH HE dimidia
quo〈que〉 eſt ipſius LE, ſiquidem LH, HE inter ſe ſunt ęqua
les; erit igitur ST vnicui〈que〉 LH, & HE æqualis. eodem què
prorſus modo oſtendeturi TV ęqualem eſſe vnicui〈que〉 HE
EC. & VX æqualem EC. & CG. & quoniam omnes
1LH, HE, EC, CG, inter ſe ſunt æquales; erunt ST TV VX in
terſe æquales. quare lineæ inter centra grauitatis magnitudi­
num STVX exiſtentes ſunt inter ſe ęquales. omnes verò magni
tudines STVX ſimul ſunt æquales ipſi A, quandoquidem ipſis
OPQR, & numero, & magnitudine ſunt ęquales; ergo magni­
tudinis ex omnibus magnitudinibus STVX compoſitæ centrumgra
uitatis erit punstum E. cùm omnes magnitudines STVX ſint nu­
mero pares. quippe cùm ſint in ſectionibus LH HE EC CG nu
mero paribus. & LE ipſi EG æqualis exiſtat. quòd ſi LE eſtipſi
EG æqualis, demptis æqualibus LS GX æqualibus, ſiquidem
ſunt dimidiæ ſectionum LH CG æqualium: erunt SE in­
terſe æquales, vnde ex præcedenti colligitur, punctum E cen­
trum eſſe grauitatis magnitudinum STVX. ſimiliter autem oſtem
detur, quòd ſi diuidatur GK in partes GD DK ipſi N æquales;
cadetvti〈que〉 diuiſionum aliqua in puncto D; ſiquidem Nipſas
GD DK metitur; cùm vtra〈que〉 ſit æqualisipſi EC. diuiſioneſ­
què GD DK numero pares erunt; cùm N dimidiam
GK, ipſam ſcilicet EC metiatur. ſi ita〈que〉 diuidatur GD DK
bifariam in punctis ZM. deinde diuidatur magnitudo B
in partes ipſi F æquales; ſectiones GD DH in GK exiſtentes
ipſi N æquales, erunt numero æquales ſectionibus in ma
gnitudine B exiſtentibus ipſi F æqualibus. quare vnicui〈que〉
partium ipſius GK apponatur magnitudo æqualis ipſi F; centrum gra­
uitatis habens in medio ſectionis; vt ponantur magnitudines ZM in
ſectionibus GD DK, ita vt magnitudinum centra grauita­
tis, quæ ſint ZM, in medio ſectionum GD DK, in punctis
nempè ZM ſint conſtituta, omnes autem magnitudines ZM ſi
mul ſunt æquales ipſi B. magnitudinis ex omnibus magnitudinibus
ZM compoſitæ centrum grauitatis erit punctum D. cùm ſit ZD
ęqualis DM. ſed magnitudines STVX ſunt magnitudini A
æquales, & ZM ipſi B ergo magnitudo A eſt tanquam impoſita
ad E, ipſa verò B ad D. eodem ſcilicet modo ſe habebit ma­
gnitudo A impoſita ad E, vt ſe habent magnitudines STVX;
ipſa verò B ſe habebit ad D, vt magnitudines ZM. ſunt au
tem magnitudines STVXZM inter ſe æquales, cùm vnaquæ 〈que〉 ſit
ipſi F ęqualis: ſuntquè omnes, (hoc eſt ipſarum centra graui
tatis) inrecta linea poſitæ; quarum centragrauitatis poſita ſunt inter ſe
1æqualiter diſtantia; ſiquidem oſtenſum eſt ST TV VX inter­
ſe æquales eſſe. Eodemquè modo oſtendetur XZ ZM cæteris
æquales eſſe. & ſunt magnitudines STVXZM numero pares,
cùm ſectiones totius LK, ( in quibus inſunt) ipſi N æquales
ſint inter ſe ęquales, & numero pares. cùm oſtenſum ſit ſectio
nes in LG, & in Gk exiſtentes numero pares eſſe. conſtat magni­
tudinis ex omnibus STVXZM magnitudinibus compoſitæ centrum
grauitatis eſſe medietatem restæ lineæ, in qua centra grauitatis magnitu
dinum habentur. Ita〈que〉 cùm LE ſit æqualis C D, EC verò ipſi Dk,
tota LC æqualis erit CK. cùm autem ſint LHDK æquales; ſi­
quidem ſunt eidem N æquales, & harum medietates, hoc eſt
LS ipſi MK ęqualis erit. & ob id SC ipſi CM eſt æqualis.
at verò linea SM magnitudinum centra grauitatis coniungit,
ergo magnitudinis ex omnibus STVXZM magnitudinibus compoſi
tæcentrum grauitatis est punctum C. Quare loco magnitudinum
STVX, poſito centro grauitatis A ad E, B verò loco ipſarum
ZM poſito ad D, erit punctum C grauitatis centrum ma­
gnitudinis ex vtriſ〈que〉 magnitudinibus AB compoſitæ. ac
prop terea ex puncto C æ〈que〉ponderabunt. ergo magnitudines AB
ex diſtantijs DC CE, quę permutatim eandem habent pro.
portionem, vt grauitates, ę〈que〉ponderant. quod demonſtrare
oportebat.
ex 3 de­
cimi.
11 quinti.
cor. 4. quin
ti.
22. quinti.
iemme.
ex 2. cor.
lemma.
2.cor. quin
tæ huius.
*
39[Figure 39] 40[Figure 40]
SCHOLIVM.
Circa finem Gręcus codex habet, τα κέντ<10>α τῶν μέσων μεγεθῶν,
quaſi dicat, centrum grauitatis magnitudinis ex omnibus
magnitudinibus STVXZM compoſitę medietatem eſſe rectę
lineę VX, quę centra mediarum magnitudinum VX coniun
git; quòd cùm ſint omnes magnitudines numero pares; itidem
eſſet punctum C, & quamuis hoc ſit verum, non tamen ad hoc
reſpexit Archimedes duabus de cauſis. Nanin ſecudo corollario
pręcedentis oſtendit centrum grauitatis omnium magnitu­
dinum eſſe medietatem rectę lineę, quę grauitatis centra om­
nia coniungit. Deinde concludere volens punctum C centrum
eſſe grauitatis omnium magnitudinum, ſtatim inquit hoc ſe
qui, quia LC eſt ipſi CK ęqualis, quę ſunt medietates totius
1rectælineę LK. Et non dixit, quia VC ſitipſi CX ęqualis.
Quare codicem græcum ita reſtituendum cenſeo. τὰκέντ<10>κ τῶν
τοῦ βὰ<10>εος μεγεθῶν, vt vertimus.
*
Ob ſe〈que〉ntis verò demonſtrationis cognitionem, hoc pro
blema priùs oſtendemus.
PROBLEMA.
Duarum expoſitarum magnitudinum incommenſurabi­
lium altera vtcum〈que〉 ſecetur; magnitudinem tota ſecta ma­
gnitudine minorem, & altero ſegmentomaiorem, alteri ve­
rò expoſitæ magnitudini commenſurabilem inuenire.
Sint duæ magnitudi­
nes incommenſurabiles

AE BC. ſeceturquè ipſa­
rum altera, putà BC, vt­
cum〈que〉 in D. oportet
magnitudinem inuenire
minorem quidem BC,
maiorem verò BD, quæ ſitipſi AE commenſurabilis. Au­
feratur ab AE pars dimidia, rurſus dimidiæ partis ipſius AE
dimidia auferatur; & eius, quæ remanet, adhuc dimidia; idquè
ſemper fiat, donec relinquatur magnitudo minor, quàm DE.
quod quidem perſpicuum eſt poſſe fieri ex prima decimi Eu­
clidis propoſitione. ſitita〈que〉 AF, quæ minor exiſtat, quàm
DC. quippe quę AF, cùm ſit abla ta ex AE ſemper per dimi
diam partem, metietur vti〈que〉 AF ipſam AE. Deinde mul­
tiplicetur AF ſuper BD, tum demum multiplicatio vltima,
vel in puncto D cadet, vel minus. ſi cadet; ſeceturex DE
magnitudo DG ęqualis AF. quod quidem fiet, quoniam AF
minor eſt DC. Quoniam igitur AF metitur BD, & DG;
metietur AF totam BG. Sed & ipſam AE metitur; etgo
AF ipſarum BG AE communis exiſtit menſura, ac propte­
rea BG ipſi AE commenſurabilis exiſtir; quæ quidem BG
minor eſt BC, maior verò BD. Si verò multi­
plicatio ipſius AF ſuper BD non cadet in D. ſed in H,
erit vti〈que〉 HD minor AF. nam ſi HD ipſi AF eſſet ęqualis,
1vltima multiplicatio caderet in D. ſi verò maior eſſet HD,
quàm AF tunc non eſſet vltima multiplicatio. quare cùm ſit
DC maior AF; erit & HC ipſa FA maior. ſi ita〈que〉 fiat HK
æqualis AF; erit punctum K inter puncta DC. BK igitur
minor erit, quàm BC, & maior BD; eodemquè modo o­
ſtendetur AF ipſarum Bk AE communem eſſe menſu­
ram. & obid BK ipſi AF commenſurabilem exiſtere. quod
facere oportebat.
1.def.deci­
mi.
41[Figure 41]
Cùm autem verba ſe〈que〉ntis demonſtrationis aliquantu­
lum ſint obſcura, vt vim demonſtrationis rectè petcipiamus,
hoc quo〈que〉 theorema ex ijs, quæ ab Archimede hactenus de­
monſtrata ſunt, oſtendemus. ad quod demonſtrandum com
muni notione indigemus, quam nos in noſtro Mechanico­
rum libro poſuimus. Nempè.
Quæ eidem æ〈que〉pondeiant, inter ſe æquè ſunt grauia.
PROPOSITIO.
Si commenſurabiles magnitudines minorem habuerint
proportionem, quàm diſtantię permutatim habent; vt ę〈que〉­
ponderent, maiori opus erit magnitudine, quàm ſit ea, quę
ad alteram magnitudinem minorem proportionem habet.
42[Figure 42]
Sint magnitudines AC commenſurabiles, diſtantię ve­
rò ſint ED EF. minorem autem habeat
1portionem A ad C, quàm ED ad EF. Dico, vt magnitu­
dines ex diſtantijs ED EF æ〈que〉ponderent, maiori o­
pus eſſe magnitudine in F, quàm ſit magnitudo A;
ita vt ipſi C in D æ〈que〉ponderare poſſit. fiat ED
ad EG, vt magnitudo A ad magnitudinem C.
Deindefiat EK æqualis EG. exponaturquè altera ma­
gnitudo L ipſi A ęqualis. Quoniam igitur minorem
habet proportionem A ad C, quàm ED ad EF, &
vt A ad C, ita ED ad EG; habebit ED ad
EG minorem proportionem, quàm ad EF. ac
EF minor eſt, quàm EG. quoniam ausem A ad C
eſt, vt ED ad EG, commenſurabiles magnitudines
AC ex diſtantijs ED EG æ〈que〉ponderabunt.
verò EK ſit æqualis EG, magnitudines AL æ­
quales ex diſtantis æqualibus EK EG ſimiliter æ〈que〉­
ponderabunt. At verò quoniam C in D æ〈que〉­
ponderat ipſi A in G, ſimiliter L in K eidem A in
G ę〈que〉ponderat; ęqualem habebit grauitatem C in D,
L in K. Ita〈que〉 quoniam diſtantia EG æqualis eſt diſtan
tiæ Ek, longitudo EK maior erit longitudine EF. ergo
magnitudines AL ęquales ex inæqualibus diſtantijs
EF non ę〈que〉ponderabunt. ſed magnitudo L deorſum ver­
get. ſi igitur in F collocanda ſit magnitudo, quæ æ〈que〉pon
deret ipſi L in K, proculdubiò hęc magnitudine A ma­
ior exiſtet. Inæqualia enim grauia, nempè L, &
do maior, quàm A, exinæqualibus diſtantijs EK EF æ­
〈que〉ponderant, dummodo maius, hoc eſt magnitudo maior,
quàm A, ſit in diſtantia minori EF. minusverò, hoc eſt ma­
gnitudo L, ſit in minori EK. Quoniam ita〈que〉 magnitudo
C in D eſt ę〈que〉grauis, vt L in K, magnitudo, quæ in F
ipſi L in K æ〈que〉ponderat, eadem quo〈que〉 in F ipſi C in D
æ〈que〉ponderabit maior verò magnitudo, quàm ſit A, in F ipſi
L in K æ〈que〉ponderat, ergo maior magnitudo, quàm A in
F, ipſi C in D æ〈que〉ponderabit. quod demonſtrare opor­
tebat.
10. quinti.
6. huius.
comm. not.
2. poſt bu­
ius.
3. huius.
His cognitis poſſumus ad Archimedis demonſtrationem
accedere.
1
PROPOSITIO. VII.
Si autem magnitudines fuerint incommenſura
biles, ſimiliter æ〈que〉ponderabunt ex diſtantijs per
mutatim eandem, at〈que〉 magnitudines, propor­
tionem habentibus.
43[Figure 43]
Sint incommenſurabiles magnitudines AB C. Distantiæ verò
DE EF. Habeat autem AB ad C proportionem eandem, quam di
stantia ED ad ipſam EF. Dico, ſi ponatur AB ad F, C ve­
rò ad D, magnitudinis ex vtriſ〈que〉 AB C compoſitæ centrum gra
uitatis eſſe punctum E. ſi enim non æ〈que〉ponderabit (ſi fieri poteſt)
AB poſita ad F ipſi C poſitæ ad D; velmaior est AB, quàm C, ita
vt AB ad F æ〈que〉ponderet ipſi C ad D; vel non. Sit maior; ſitquè
exceſſus HL; ita vt KH ad F, & C ad D ę〈que〉ponderent.
auferaturquè ab ipſa AB magnitudo NL, quæ ſit minor exceſſu
HL, quo maior est tota AB, quàm C, ita vt æ〈que〉ponderent; vt dictum
eſt. & ſit quidem reſiduum A, hoc eſt KN, commenſurabile ipſi C.
Et quoniam minor eſt kN quàm KM, minorem quo〈que〉
1habebit proportionem kN ad C, quàm kM ad eandem
C. tota verò KM ad C eſt, vt DE ad EF; ergo KN ad
C minorem habet proportionem; quàm DE ad EF. Quo
niam igitur magnitudines AC, hoc eſt KN C, ſunt commenſurabi­
les, & minorem habet proportionem A, hoc eſt kN ad C, quàm DE
ad EF; non æ〈que〉ponderabunt A C, hoc eſt KN C, ex distantiis
DE EF, poſito quidem A, hoc eſt KN ad F, C verò ad D. &
vt æ〈que〉ponderent, oporter, vt in F maior ſit magnitudo,
quàm KN; ita vt ipſi C in D æ〈que〉ponderate poſſit. Ac
propterea cùm ſit kH adhuc minor, quàm KN, ſi igitur
KH ponatur ad F, & C ad D, nullo modo æ〈que〉ponde­
rabunt. quod tamen fieri non poteſt. ſupponebatur enim eas
æ〈que〉ponderare. Non igitur magnitudo minor, quàm tota
KM in F magnitudini C in D æ〈que〉ponderat. Eadem au­
tem ratione, ne〈que〉 ſi C maior fuerit, quàm vt æ〈que〉ponderet ipſi AB,
hoc eſt ipſi KM. etenim grauiore exiſtente C ad D, quàm KM
ad F. primùm auferatur ex C exceſſus, quo C grauior eſt,
quàm KM, ita vt æ〈que〉ponderet ipſi KM. Deinde rurſus
auferatur quædam magnitudo minor exceſſu, quo grauior
eſt C, quàm kM, ita vt æ〈que〉ponderent; reſiduum verò ſit
ipſi KM commenſurabile, & c. ſimiliter oſtendetur nullam
magnitudinem ipſa C minorem poſitam ad D vllo modo
æ〈que〉ponderare ipſi KM ad F poſitæ. Quare magnitudo
C ad D, kM verò ad F ę〈que〉ponderant. Vnde ſequitur ma
gnitudinis ex vtriſ〈que〉 magnitudinibus compoſitæ centrum
grauitatis eſſe punctum E. ac propterea incommenſurabiles
magnitudines AB C ex diſtantiijs ED EF, quæ permutatim
eandem habent proportionem, vt magnitudines, æ〈que〉pon­
derare. quod demonſtrare oportebat.
ex proxi­
mo proble­
mate.
8. quinti.
ex præce­
denti.
ex prima
propoſitio­
ne.
SCHOLIVM.
In demonſtratione occurrit obſeruandum, quòd ſi exceſ­
ſus HL ita diuideret magnitudinem KM, vt reſiduum KH
fuerit commenſurabile ipſi C; tunc abſ〈que〉 alia conſtructio­
ne, magnitudines commenſurabiles KH C ex diſtantijs DE
EF æ〈que〉ponderarent; quod fieri non poteſt. cùm minorem
1habeat proportionem KH ad C, quàm ED ad EF. ſiquidem
ſupponitur KM ad C ita eſſe, vt ED ad EF. Archimed es ve
iò, vt demonſtratio abſ〈que〉 diſtinctione ſit vniuerſalis, prę­
cipit (exiſtente KH ipſi C commenſurabili, ſiue incommen
ſurabili) vt auferatur pars aliqua minor exceſſu HL, ut AL,
ita tamen, vt reliqua KN ſit commenſurabilis ipſi C. quod qui
dem fieri poſſe oſtenſum eſt in proximo problemate. ex tota
enim magnitudine KM partem abſcindere poſſumus, vt KN
minorem quidem tota KM, maiorem verò KH, quæ ipſi
C commenſurabilis exiſtat.
Cognita Archimedis demonſtratione de incommenſura­
bilibus magnitudinibus, idem alio quo〈que〉 modo oſtendere
poſſumus, applicando nempè diuiſibilitatem, & commenſura
bilitatem non magnitudinibus, verùm diſtantijs. hac autem
priùs demonſtrata propoſitione.
PROPOSITIO.
Si commenſurabiles diſtantię maiorem habuerint pro­
portionem, quàm magnitudines permutatim habent; vt
ę〈que〉ponderent, maiori opus erit longitudine, quàm ſit
ea, ad quam altera longitudo maiorem habet proportio­
nem.
44[Figure 44]
Sint diſtantiæ DE EH commenſurabiles, magnitudines
verò ſint A C. habeatquè ED ad EH maiorem proportio­
nem, quàm A ad C. Dico vt AC ę〈que〉ponderent, maiori opus
1eſſe longitudine, quàm ſit EH. exponatur altera magnitu­
do G, quæ ad C eandem habeat proportionem, quàm habet
DE ad EH. erunt vti〈que〉 magnitudines GC inter ſe commen
ſurabiles. Deinde fiat EK æqualis EH, exponaturquè ma­
gnitudo L ipſi G æqualis. Quoniam igitur G ad C eſt,
vt DE ad EH, ob commenſurabilitatem æ〈que〉pondera
G in H, & C in D. ſimiliter æ〈que〉pondera bunt magnitudi­
nes æquales GL ex æqualibus diſtantijs EK EH. Cùm igitur
C in D ipſi G in H æ〈que〉ponderet; L verò in K ipſi quo­
〈que〉 G in H æ〈que〉ponderet; eandem habebit grauitatem
in D, ut L in K. Quoniam autem maiorem habet propor­
tionem DE ad EH, quàm A ad C, & vt DE ad EH, ita eſt
G ad C; maiorem habebit proportionem G ad C, quàm A
ad C. ergo maior eſt G, quàm A. ac propterea magnitudo
minor eſt magnitudine L. poſita igitur magnitudine L in K,
& A in H, non æ〈que〉pondera bunt; & vt ę〈que〉ponderent, o­
portet, vt A in longiori ſit diſtantia, quàm ſit EH: Inęqualia
enim grauia LA ex inęqualibus diſtantijs
maius quidem L in minori diſtantia EK, minus verò graue
A in maiori, quàm ſit EK, hoc eſt in maiori, quàm ſit EH.
Ita〈que〉 cùm ſit C in D æ〈que〉grauis, vt L in k; longitudo,
quæ efficit, vt A æ〈que〉ponderetipſi L in K; eadem prorſus
efficiet, vt A ipſi C in D ę〈que〉ponderare poſſit. A verò in
maiori diſtantia, quàm EH, ipſi L in K ę〈que〉ponderat; ergo
in maiori diſtantia, quàm EH, magnitudo A ipſi C in D
ę〈que〉ponderabit. quod demonſtrare oportebat.
6. buius.
communis no
tio ſupradi
cta.
10. quinti.
3. huius.
Hoc demonſtrato Archimedis propoſitionem de incom­
menſurabilibus magnitudinibus aliter oſtendemus hoc
pacto.
ALITER.
Incommenſurabiles magnitudines ex diſtantijs permuta­
tim eandem, at〈que〉 magnitudines, proportionem habenti­
bus; ę〈que〉ponderant.
1
Sint incom­

menſurabiles ma
gnitudines AC,
diſtantiæ verò
DE EF. ſitquè vt
A ad C, ita DE
ad EF. Dico A
in F, C verò in
D æ〈que〉ponde­
rare. Si autem (ſi fieri poteſt) non æ〈que〉pondera bunt; diſtam
tiæ DE EF aliter ſeſe habere debebunt, vt magnitudines AC
ę〈que〉ponderent. Quocirca vel longior eſt EF, quàm opus
ſit, vel longior eſt ED. ſit EF longior. ſitquè exceſſus GF, ita
vt poſita magnitudine A in G ipſi C in D æ〈que〉ponde­
 ret. Fiat EH maior EG, minor verò EF. ſit autem EH
ipſi ED commenſurabilis. Quoniam igitur DE ad EH
maiorem habet proportionem, quàm ad EF; & vt DE ad
EF, ita eſt A ad C; maiorem habebit proportionem DE
ad EH, quàm A ad C. ſuntquè longitudines ED EH in­
terſe commenſurabiles; ergo magnitudo A in H ipſi C in
D non æ〈que〉ponderabit, ſed vt ę〈que〉ponderet, maiori opus
eſt longitudine, quàm ſit EH; ita vt A ipſi C in D æ〈que〉
ponderare poſſit. at〈que〉 adeò cùm adhuc minor ſit EG, quàm
EH; magnitudo A in G magnitudini C in D nullo modo
æ〈que〉ponderabit. quod fieri non poteſt. ſupponebatur enim
A in G, & C in D ę〈que〉ponderare. eademquè prorſus ra­
tione, ſi ED longior fuerit, quàm opus ſit, ita vt magnitu­
dines æ〈que〉ponderent, oſtendetur magnitudinem C nullo pa­
cto æ〈que〉ponderare poſſe ipſi A in F in minori diſtantia,
quàm DE. Quare magnitudines in commenſurabiles AC ex
diſtantijs ED EF, quæ eandem permutatim habent propor­
tionem, vt magnitudines, æ〈que〉ponderant. quod demonſtra­
re oportebat.
problema
ante 7. bu­
ius 8. quinti
ex pxima
ppoſitione
45[Figure 45]
In prioribus ſermonibus ante quintam propoſitionem ha­
bitis, diximus propoſitionum præcedentium demonſtratio­
nes planiores euadere, ſi intelligamus magnitudines eiuſdem
eſſe ſpeciei, & homogeneas. Quòd quidem ſi Archimedem
1his, vel de rectilineis tantùm demonſtrationes attuliſſe (vt non­
nulli fortaſſe falsò exiſtimarunt) intelligeremus; ita vt ex Ar­
chimedis demonſtrationibus non ſit adhuc vniuerſaliter de­
monſtratum hoc pręcipuum fundamentum; nempè magni­
tudines ex diſtantijs permutatim proportionem habentibus, vt
ipſarum grauitates, ę〈que〉ponderare; in hoc certè rationes ab
Archimede allatas, ipſarum què demonſtrationum vim mini­
mè percipiemus. Quapropter ea, quæ demonſtrauit, omni­
bus magnitudinibus vniuerſaliter competere ipſum voluiſſe
nullatenus eſt dubitandum. Ne〈que〉 enim, vt perfectè, & vni­
uerſaliterſciamus, magnitudines ç〈que〉ponderare ex diſtantijs
permutatim proportionem habentibus, vt ipſarum grauita­
tes, alijs, quàm pręcedentibus propoſitionibus indigemus.
In hoc enim fundamento demonſtrando minimè diminu­
tus extitit Archimede. Nam ſi ad propoſitiones ab ipſo alla­
tas, pręcipuèquè ad vim demonſtrationum reſpiciamus, ſiuè
magnitudines intelligantur eiuldem ſpeciei, ſiue diuerſę, ſi­
ue homogeneę, ſiue heterogeneę, ſiue planę, ſiue ſolidę, &
hę quidem, ſiue rectilineę, ſiue quom odocun〈que〉 mixtę; ni­
hilominus demonſtrationes idem prorſus concludent, ita vt
Archimedes non de aliquibus magnitudimbus tantùm de­
monſtrationes attulerit; ſed de omnibus prorſus demonſtra­
uerit. In his enim Archimedes non ad magnitudines tantùm,
verùm ad magnitudinum grauitates potiſſimùm reſpexit.
quandoquidem loco grauium magnitudines nominat; vt
poſt quartam huius propoſitionem adnotauimus. quod qui­
dem facilè ex verbis ipſius rectè intellectis apparere poteſt. Nam
in quærta propoſitione cùm inquit, ſi duæ fuerint magnitudines
æquales, vt antea diximus, intelligendum eſt eas ęquales
eſſe grauitate. quod non ſolùm ex eius demonſtrationeli­
〈que〉t, verùm etiam ex modo lo〈que〉ndi, quo vſus eſt Archime­
des in alijs propoſitionibus. In quinta enim propoſitione,
quę eiuſdem eſt cum quarta ordinis, & naturę, in quit;
Sitrium magnitudinum centra grauitatis in recta linea fuerint poſi­
ta, & magnitudines æqualem habuerint grauitatem. ſimlli­
ter poſt quintam demonſtrationem bis quoquè eodem v­
titur lo〈que〉ndi modo, nempè cùm adhuc proponit
1plures magnitudines, inquit, & magnitudines æqualem habuerint
grauitatem. ex quibus conſtat Archimedem ad magnitudinum
grauitates omnino reſpexiſſe. ita vt quando Archimedes in­
quit, & magnitudines æquales, idem eſt, ac ſi dixiſſet, & magnitu­
dines æqualem habuerint grauitatem. Præterea in ſexta propoſitio
ne inquit magnitudines ę〈que〉ponderare ex diſtantijs permu­
tàtim proportionem habentibus, vt grauitates. ita ut cauſa
huius æ〈que〉ponderationis ſit (vt reuera eſt) magnitudinum
grauitas. & quanquam in hac ſeptima propoſitione dicat, ma
gnitudines æ〈que〉ponderare ex diſtantijs permutatim propor­
tionem habentibus, vt magnitudines, & non dixit, vt grauita
tes; intelligendum tamen eſt, ac ſi dixiſſet, eas ę〈que〉pondera­
re, vt magnitudinum grauitates. hęc enim ſeptima propoſi­
tio eſt pars ſextæ propoſitionis, vt iam pręfati fum^{9}; vnde ſi in
ſexta magnitudines ę〈que〉ponderant ob earum grauitatem, ob
eandem quo〈que〉 cauſam & in hac ſeptima æ〈que〉ponderare de
bent. Pręterea in ſe〈que〉nti etiam propoſitione dum proponit
oſtendere quam proportionem habere debent ſectiones lineę
intercentra grauitatum diuiſę magnitudinis exiſtentes, inquit,
quam habet grauitas magnitudinis ablatæ ad grauitatem reſiduæ hoc
autem deinceps exponens, non inquit oportere ſectiones lineæ
eam habere proportionem, quàm grauitas ad grauitatem ha­
bet; ſed horum loco inquit, quàm magnitudo ad magnitudi
nem. ex quibus omnibus clarè perſpicitur, quòd quando Ar­
chimedes magnitudines nominat, omnino magnitudinum
grauitates vult intelligere.
Ad eorum autem intelligentiam, quę dicta ſunt in ſexta, ſepti
maquè propoſitione, earunquè demonſtrationibus, obſeruandum
eſt, quòd in ſexta propoſitione pro magnitudinibus commen
ſurabilibus intelligere oportet magnitudines grauitate com­
menſurabiles; ita nempe, vt numeris exprimi poſſint; quam­
quam non ſint mole, & magnitudine commenſurabiles, vt
in figura ſextę propoſitionis magnitudo A ponderet exempli
gratia vt XVI. B verò vt VIII. intelligatur〈que〉; F magnitudinum
1AB communis menſura in grauitate, ita vt ſit æ〈que〉grauis vni­
cui〈que〉 parti OPQR, quæ quidem, & ſi non ſint magnitu­
dine inter ſe ęquales, ſufficit, vt ſint æ〈que〉graues: veluti magni

tudines quo〈que〉 STVX inter ſe, ipſis〈que〉; OPQR tantùm ę〈que〉
graues; ita ut vnaquæ〈que〉 ponderet, vt IIII. veluti etiam par
tes ipſius B, & vnaquæ〈que〉 ZM. hiſquè ita poſitis demonſtra
tio rectè concludet.
46[Figure 46]
In hacverò ſeptima Archimedis propoſitione in­
telligantur magnitudines kMC incommenſurabiles graui­
tate, vt in eius figura grauitas ipſius C ponderet, vt XII. gra
uitas verò ipſius KM maior ſit, quàm XX. ita vthę graui­
tates ſint in commenſurabiles. auferaturquè grauitas exceſſus
HL, quæ ſit vt IIII. ita vt quæ relinquiturgrauitas, ipſius nen­
pè KH, quę quidem maior eſt, quàm XVI, in F poſita, gra
uitati ipſius C, quæ eſt XII, in D poſitæ æ〈que〉ponderet,
Auferatur deinde NL minor exceſſu HL; cuius quidem gra
uitas ſit maior, quàm II. ita vt grauitas reſidui KN, quæ
nimirum ſit XVIII, ſit commenſurabilis grauitati
XII. ipſius C. & quamuis magnitudines KM C, & KN C ſint,
vel non ſint inter ſe magnitudine commenſurabiles, vel
1menſurabiles; eadem prorſus demonſtratio idem concludet.
quæ quidem omnia in ſe〈que〉nti quo〈que〉 propoſitione conſi­
deranda occurrunt. Vnde perſpicuum eſt has Archime dis pro
poſitiones, ac demonſtrationes vniuerſaliſſimas eſſe, ar〈que〉 o­
mnibus, & quibuſcun〈que〉 magnitudinibus conuenientes.
reſpice fi­
guram ſepti­
mæ propoſi
tionis Ar­
chimedis.
Iacto hoc pręcipuo, ac pręſtantiſſimo mechanico funda­
mento; in ſe〈que〉nti propoſitione colligit ex hoc Archimedes,
quomodo ſe habent centra grauitatis magnitudinis diuiſæ.
PROPOSITIO. VIII.
Si ab aliqua magnitudine magnitudo aufera­
tur; quæ non habeat idem centrum cum tota; re­
liquæ magnitudinis centrum grauitatis eſt in re­
cta linea, quæ coniungit centra grauitatum to tius
magnitudinis, & ablatæ, ad eam partem produ­
cta, vbi eſt centrum to tius magnitudinis, ita vt aſ­
ſumpta aliqua ex producta, quæ coniungit centra
prædicta eandem habeat proportionem ad eam,
quæ eſt inter centra, quam habet grauitas magni­
tudinis ablatæ ad grauitatem reſiduæ, centrum e­
rit terminus aſſumptæ.
Sit alicuius magnitudinis AB centrum grauitatis C. auferatur­
què ex AB magnitudo AD; cuius centrum grauitatis ſit E. coniuncta
verò EC, & ex parte C producta, aſſumatur CF, quæ ad CE eam
dem habeat proportionem, quam habet magnitudo AD ad DG. osten­
dendum est, magnitudinis DG centrumgrauitatis eſſe punctum F. non
ſit autem; ſed, ſi fieri potest, ſit punctum H. Quoniam igitur magnitudi­
nis AD centrum grauitatis est punctum E; magnitudinis verò DG
eſt punctum H; magnitudinis ex vtriſ〈que〉 magnitudinibus AD DG,
compoſitæ centrum grauitatis erit in linea EH, ita diuiſa, ut pirtes ipſius
permutatim eandem habeant proportionem, vt magnitudines. Quare non
1erit punctum C ſecundùm diuiſionem proportione reſpondentem prædi­
etæ. vt ſcilicet ſit HC ad CE, vt AD ad DG. etenim ut AD
ad DG; ita factum fuit FC ad CE. ſi igitur ſecetur linea EH ſe
cundùm proportionem ipſius AD ad DG; non terminabit

diuiſio ad punctum C. cùm ſit impoſſibile eandem habere
proportionem FC ad CE, quam. HC ad eandem CE. di­
uiſio igitur ad aliud terminabitur punctum, vt K; ita vt
ad KE ſit, vt AD ad DG. vnde ſequitur punctum K cen­
trum eſſe grauitatis magnitudinis ex AD DG compoſitæ.
Non eſt igitur punctum C centrum magnitudinis ex AD DG compo
ſitæ; hoc est ipſius AB. eſt autem; ſuppoſitum eſt enim ipſum eſſe. er­
go ne〈que〉 punctum H centrum est grauitatis magnitudinis DG. eſt
igitur punctum F; quod quidem eſt terminus productę lineę
CF; quæ eandam habet proportionem ad lineam CE inter
centra exiſtentem; quam habet grauitas magnitudinis AD
ad grauitatem ipſius DG. quod demonſtrare oportebat.
ex præce­
dentibus.
ex præce­
dentibus.
47[Figure 47]
SCHOLIVM.
In hac demonſtratione intelligendum eſt etiam punctum
H eſſe poſſe extra lineam EF, ita vt EFH non ſitirecta linea.
quòd ſi H non eſſet in linea EF, idem ſequi abſurdum adeò
perſpicuum eſt; vt nec demonſtratione egeat. Quoniam ſi in
telligatur H extra lineam EF; iuncta EH, & ita diuiſa intel­
ligatur, vt ipſius partes permutatim grauitatibus magnitudi­
num AD DG reſpondeant; eſſet vti〈que〉 hoc punctum inuen­
tum, quod extra lineam EF reperiretur, centrum grauitatis to
1tius AB quod fieri non poteſt. ſiquidem eſt punctum C, vt
ſuppoſitum fuit. Vnde ne〈que〉 illud punctum H ipſius DG cem
trum grauitatis exiſteret.
Hic eſt terminus primę partis principalis, in qua Archime
des (vt initio dixim^{9}) de magnitudinib^{9}, & degrauibus in
communi pertractauit; quandoquidem propoſitiones, ac de­
monſtrationes tam planis, quàm ſolidis quibuſcun〈que〉 ſunt
accomodatæ; vt manifeſtum fecimus.
Nunc ita 〈que〉 ſe conuertit Archimedes ad inueſtigandum cen
tra grauitatis planorum. primùm què perquirit centrum gra­
uitatis parallelogrammorum; oſtendetquè centrum grauitatis
cuiuſlibet parallelogrammi eſſe in recta linea, quæ coniungit
oppoſita latera bifariam diuiſa. ob cuius intelligentiam hæc
priùs lemmata in vnum collecta nouiſſe erit valdè vtile.
LEMMA.
Sit parallelogrammum ABCD, cuius oppoſita latera AB
CD ſint bifariam diuiſa in EF. connectaturquè EF, quæ ni
mirum æquidiſtans erit ipſis AC BD. Deinde diuidatur v­

naquæ〈que〉 AE EB in partes numero pares, & inuicem ęqua
les; vt in AG GE; & EH HB. ducanturquè GK HL ipſi
EF ęquidiſtantes. ſit verò centrum grauitatis ipſius AK pun
ctum M. ipfius verò GF punctum N, & ipſius EL pun­
ctum O deniquè ipſius HD punctum P. Dico primùm pum
cta MNOP eſſe in linea recta. deinde lineas MN NO OP
inter centra exiſtentes inter ſe æquales eſſe. Deni〈que〉 centrum
grauitatis parallelogrammi AD eſſe in linea NO, quę con
iungit centra grauitatis ſpatiorum mediorum; parallelogram
morum ſcilicet GF EL.
1Ducantur à punctis MN ipſi AGE ęquidiſtantes QMR
SNT. erunt vti〈que〉 AQRG, & GSTE parallelogramma.
Quoniam igitur parallelogramma AK GF in æqualibus
ſuntbaſibus AG GE, & in ijſdem parallelis; erunt AK
inter ſe ęqualia. & quoniam AC GK EF ſunt ęquidiſtantes;
erit angulus CAG ipſi KGE ęqualis, & KGA ipſi
æqualis; & horum oppoſiti inter ſe ſunt ęquales; paralle­
logrammum GF ipſi AK ęquale, & ſimile exiſtit. Ita〈que〉
ſi GF colloceturſuper AK, rectè congruet: eruntquè paral­
lelogramma inuicen coaptata. lineęquè GE AG, GK AC, &
reliquæ coaptatæ erunt. quare eorum centra inui­
cem coaptata erunt. hoc eſt N erit in puncto M. Quoniam
autem à punctis MN (quod nunc intelligitur vnum tantum
eſſe punctum) ductæ fuerunt ST QR ipſi AGE æquidi­
ſtantes, linea ST coaptabitur cum QR, quippe cùm ambæ
hæ lineæ ab vno puncto prodeuntes ipſi AG ęquidiſtantes
eſſe debeant. punctum igitur S in Q, & T in R coaptabi­
tur. eritquè QM ipſi SN ęqualis, & MR ipſi NT. ac pro
pterea linea GS parallelogrammi GT erit coaptata in A〈que〉
& ET coaptata erit in GR parallelogrammi AR. Vnde e­
rit AQ ęqualis GS, cùm ſint coaptatæ; & GR ipſi ET ę­
qualis; cùm ſint quo〈que〉 coaptatę. Quocirca pa­
rallelogramma AR GT ſunt inuicem coaptata, paral­
lelogrammorumquè oppoſita latera ſunt inter ſe ęqualia, erunt
AQ GS GR ET inter ſe ęqualia. Nunc autem intelligantur
parallelogramma AK GF non ampliùs coaptata. & quoniam
lineę QMR, & SNT ſuntipſi AGE parallelę; & AQ GR,
GS ET, inter ſe ſuntæquales, & ęquidiſtantes; puncta RS in
vnum coincident punctum. eritquè QST linea recta. ex qui
bus patet, rectam lineam, quæ coniungit centra grauitatis MN
ipſi AGE æquidiſtantem exiſtere. eodemquè modo oſtende­
tur rectas lineas, quæ coniungunt grauitatis centra NO, cen­
traquè OP, ipſi AB æquidiſtantes eſſe. Vnde ſequitur lineam
MNOP rectam eſſe. Quare primùm conſtat grauitatis centra
in recta linea exiſtere.
36. primi.
29. primi.
34. primi.
5. post, hu­
ius.
34. primi.
48[Figure 48]
Quoniam autem oſtenſum eſt QM æqualem eſſe ipſi SN,
& MR ipſi NT, eodem quo〈que〉 modo oſtendetur OT
1lem eſſe ipſi SN. Quoniam igitur OT NS ſunt ęquales, iti­
demquè TN SM æquales, erit ON ipſi NM æqualis. ea­
demquè ratione oſtendetur OP ęqualem eſſe ipſi ON. vn­
de colligitur lineas MN NO OP inter centra exiſtentes in­
rerſe ęquales eſſe.
Poſtremò quoniam parallelogramma AK GF EL HD
ſunt inuicem æqualia, & numero paria, centraquè grauitatis
ſunt in recta linea poſita. lineęquè MN NO OP inter cen­
tra ſunt ęquales, magnitudinis ex omnibus AK GF EL HD
magnitudinibus compoſitæ centrum grauitatis eſt in linea
MP bifariam diuiſa. Et quoniam MN eſt æqualis ipſi OP,
punctum, quod bifariam diuidit MP cadet in linea NO.
centrum ergo grauitatis omnium magnitudinum AK GF
EL HD, hoc eſt parallelogrammi AD eſt in linea NO, quę
coniungit centra ſpatiorum mediorum GF EL. quę quidem
omnia oſtendere oportebat.
2.cor. quin
tæ huius.
Quoniam autem centrum grauitatis parallelogrammi AD
eſt in linea NO, & in linea MP bifariam diuiſa; non repu­
gnare videtur, quin inferri poſſit, hoc centrum eſſe in puncto
T, in linea EF exiſtente. Quòd tamen falſum eſt. nam poſ
ſet quidem concludi centru eſſe in medio lineę NO (ſiquidem
eſt in medio lineę MP, vt dictum eſt) ſed non in puncto T; ex demom
ſtratione enim oſtenditur NS æqualem eſſe ipſi TO. at verò
NT ęqualem eſſe ipſi TO, nullo modo demonſtrari poteſt;
niſi ſupponeremus centra grauitatis MNOP in parallelogra
mis ita ſe habere, vt MQ MR, & MR RN, & RN NT &
NT TO, &c. inter ſe ęquales eſſent. quod nullo modo ſup­
poni poteſt nam hoc modo centra grauitatis parallelogram­
morum AK GF &c. eſſent in lineis, quę bifariam ſecant op
poſita latera. eſſent quippè in lineis à punctis MN OP du­
ctisipſis AC GK EF &c. æquidiftantibus, quæ oppoſita la
tera AG CK, GE KF, EH FL, &c. bifariam ſecarent. quod
eſt id, quod Archimedes demonſtrare in ſe〈que〉nti nititur. quod
quidem in cauſa eſt, vt demonſtratione ad impoſſibile id de­
ducat. ſuppoſuimus autem (vt pareſt) parallelogramma
1tra grauitatis habere; ac centra grauitatis MNOP intra pa­
rallelogramma exiſtere, quoniam parallelogramma fi­
guræ ad eaſdem partes concauæ. quod quidem eodem modo
ab Archimede in ſe〈que〉nti ſupponitur.
9. poſt hu­
ius.
PROPOSITIO. IX.
Omnis parallelogrammi centrum grauitatis
eſt in recta linea, quæ oppoſita latera parallelo­
grammi bifariam diuiſa coniungit.
49[Figure 49]
Sit parallelogrammum ABCD, linea verò EF bifariam diuidat la
tera AB CD. Dico parallelogrammi ABCD centrum grauitatis eſſe
in linea EF. Non ſit quidem, ſed, ſi fieri poteſt, ſit H. & ab ipſo vſ〈que〉
ad lineam EF ducatur H æquidistansipſi AB. Diuiſa verò EB
ſemper bifariam in G. rurſuſquè EG brfariam in K; idèquè
ſemper fiat, tandem quædam relin〈que〉tur linea, putà EK, minor
ipſa HI. Diuidaturquè vtra〈que〉 AE EB in partes AN NM
LE GO OB ipſi EK æquales. quod quidem fieri poteſt, quia
diuiſa eſt EB in partes ſemper ęquales. & ex his diuiſionum pun
ctis ducantur NP MQ LR kS GT OV ipſi EF æquidistantes.
diuiſum enim erit totum parallelogrammum in parallelogramma æqualia
& ſimiliaipſi kF. cùm enim ſint parallelogrammorum baſes
EL LM MN NA KG GO OB ipſi KE parallelo­
grammaquè in ijſdem ſint parallelis AB CD conſtituta;
erunt parallelogramma æqualia. ſimilia verò, quoniam
ſunt ęquiangula. Parallelogrammis igitur æqualibus, at〈que〉
1ſimilibus ipſi KF inuicem coaptatis, & centra grauitatis inter ſe conue­
nient. quia verò in EB facta eſt diuiſio ſemper in duas partes
ęquales erunt parallelogramma in ED numero paria. ac per
conſe〈que〉ns & quę ſunt in EC numero paria. vnde & quę sunt
in toto AD numero paria erunt. Jta〈que〉 quædam erunt magnitudi­
nes æquidiſtantium laterum æquales ipſi KF numero pares, hoc eſt o­
 mnes, quæ ſunt in AD, centraquè grauitatis ipſarum in recta linea
ſunt conſtituta, & lineæ inter centra ſunt a quales magnitudinis ex ipſis
omnibus compoſitæ centrum grauitatis erit in recta linea, quæ coniungit
centra grauitatis mediorum ſpatiorum, parallelogrammorum ſcili­
cet LF KF. Non est autem; punctum enim H, quod ſupponitur
eſſe centrum grauitatis omnium magnitudinum, hoc eſt pa
rallelogrammi AD, extra media parallelogramma LF KF exiſtit.
etenim cùm ſit EK minor HI, linea KS ipſi EF ęquidiſtans
lineam HI ipſi EK æquidiſtantem ſecabit, quippè quæ re­
lin〈que〉t punctum H extra figuram KF, ac per conſe〈que〉ns ex­
tra media parallelogramma LF KF. quare punctum H non
eſt centrum grauitatis parallelogrammi AD, vt ſupponeba­
tur. ergo conſtat, centrum grauitatis parallelogrammi ABCD eſſe in re
cta linea EF. quod demonſtrare oportebat.
*
ex prima
pręcedenti
36. primi.
*
lemma.
SCHOLIVM.
Græcus codex poſt verba, centraquè grauitatis ipſarum in recta
linea ſunt constituta, habet, καὶ τὰ μὲσα ἴσα, καὶ ω̄ὰντα τὰ εφ̓ εκάτεζα
τῶν μἐσων αυτά τε ἴσα ἐντί, quæ quidem omnino ſuperflua nobis
uia ſunt, & tanquam ab aliquo addita. Nam ſi Archimedes di­
xit omnia parallelogramma eſſe inter ſe, & ęqualia, & ſimilia;
non opus eſt addere, media LF ES eſſe inter ſe ęqualia, &
quę ab his ſunrad vtram〈que〉 partem, vt MR KT, NQ GV,
AP OD, eſſe inter ſe æqualia; cum omnia (vt dictum eſt) ſint
ęqualia. quare verba hęc (meo quidem iudicio) delenda ſunt.
demonſtrationes enim mathematicę nullum admittunt ſu­
perfluum. & Archim edes non tantùm ſuperfluus, quin potiùs
ob cius breuitatem diminutus ferè videatur.
1
*
Ex hac nona propoſitione duo corolloria elicere poſſum^{9};
quæ quidem tanquam valde nota fortafſe videtur omiſiſſe Ar
chimedes. quamuis primum in ſe〈que〉nti demonſtratione inſeruit.
COROLLARIVM. I.
Ex hoc perſpicuum eſt cuiuſlibet parallelogrammi centrum
grauitatis eſſe punctum, in quo coincidunt rectæ lineæ, quæ
oppoſita latera bifariam ſecant.
Nam (vt Archimedes etiam ſe

〈que〉nti demonſtratione inquit)
ſi parallelogrammi ABCD lineę
EF GH bifariam diuident late­
ra oppoſita AB DC, & AD BC.
patet in EF centrum eſſe graui­
tatis parallelogrammi AC. ſimi
liter conſtat idem centrum eſſe
in linea GH, quæ oppoſita latera AD BC bifariam ſecat. e­
ritigitur in K, vbi EF GH ſeinuicem ſecant.
50[Figure 50]
COROLLARIVM. II.
Ex hoc patet etiam, cuiuſlibet parallelogrammi centrum gra
uitatis eſſe in medio rectæ lineę, quæ bifariam oppoſita latera
diſpeſcit.
Cùm enim oſtenſum ſit centrum grauitatis parallelogram
mi AC eſſe punctum K. & ob parallelogrammum EH eſt
EK æqualis BH. propter parallelogrammum verò
linea KF eſt æqualis HC. ſuntquè BH HC æqua­
les. erit EK ipſi KF æqualis. punctum ergo K eſt in medio
rectæ lineę EF, quæ oppoſita latera AB DC bifariam diui­
dit. Eoden〈que〉; prorſus modo oſtendetur, K medium eſſe rectę lineę
GH, quæ bifariam ſecat oppoſita latera AD BC.
34. primi.
In ſe〈que〉nti Archimedes adhuc perſiſtit in inuentione cen­
tri grauitatis parallelogrammorum, alia tamen methodo.
nam hoc peripſorum parallelogrammorum diametros duo­
bus modis aſſequitur.
1
PROPOSITIO. X.
Omnis parallelogrammi centrum grauitatis
eſt punctum, in quo diametri coincidunt.
Sit parallelogrammum
ABCD. & in ipſo ſit li­
nea EF bifariam ſecans

latera AB CD. itidem­
què ſit KL ſecans AC BD
bifariam. conueniant­
què EF kL in H. est
vti〈que〉 parallelogrammi
ABCD centrum grauita
tis in linea EF. hoc enim
oſtenſum eſt. eadem verò de cauſa centrum grauitatis ipſius AD est
etiam in linea KL. quare punctum H parallelogrammi AD cen­
trum grauitatis existit. Verùm in puncio H diametri parallelogram­
mi concurrunt. ductis enim lineis AH HB CH HD; quoniam
lineæ AE EB EF FD inter ſe ſunt ęquales. ſimiliter quo〈que〉
AK KC BL LD inter ſe ęquales; erit EH ipſi HF ęqua
lis, cùm ſint ipſis BL LD ęquales. duæ igitur AE EH dua
bus DF FH ſunt æquales, & angulus AEH angulo DFH
ęqualis; erit triangulum AEH triangulo DFH ęquale. ac
propterea angulus EHA angulo FHD æqualis. cùm igitur
ſit EHF recta linea, eruntangnli EHA FHD adverticem,
& obid AHD recta exiſtit linea. ac per conſe〈que〉ns diame­
ter parallelogrammi AD. pariquè ratione oſtendetur BHC
rectam eſſe lineam. ex quibus patet in puncto H vtran〈que〉 dia
metrum conuenire. centrum igitur grauitatis parallelogram­
mi AD eſt punctum, in quo diametri concurrunt. Quare demon
stratumeſt, quod propoſitum fuit.
1
9 huius.
29, primi.
4. primi.
51[Figure 51]
ALITER.
Hoc autem aliter quo­
〈que〉 oſtendetur. ſit paralle

logrammum ABCD.
ipſius verò diameter ſit
B D. triangula vti〈que〉
ABD BDC erunt in­
terſe æqualia, & ſimilia.
quare triangulis inuicem
coaptatis; centra quo〈que〉
grauitatis ipſorum inuicem coaptabuntur. Sit autem trianguli ABD cen
trum grauitatis punctum E; lineaquè BD bifariam ſecetur in H. con
nectaturquè EH, & producatur. ſumaturquè FH æqualisipſi HE.
Ita〈que〉 coaptato triangulo ABD cumtriangulo B DC, poſitoquè latere
AB in DC, hoc eſt A in C, & B in D. AD autem poſito in
BC; A ſcilicet in C, & D in B. vnde & BD cum ipſamet
DB coaptatur, B ſcilicet in D, & D in B. quia verò pun­
ctum H ſibi ipſi coaptatur, cùm fitmedium lineę BD. & an
guli EHD FHB ad verticem ſunt æquales; lineaquè EH eſt
ipſi HF ęqualis; congruet etiam recta HE cum recta FH, & pun­
ctum E cum F conueniet, ſed quoniam punctum E centrum
eſt grauitatis trianguli ABD idem punctum E cum centro e­
tiam grauitatis trianguli B DC conueniet. ergo punctum F cen­
trum eſt grauitatis trianguli BDC. Nunc verò intelligantur
triangula non ampliùs coaptata. Quoniam igitur centrum graui­
tatis trianguli ABD eſt punctum E, ipſius verò DBC est punctum F,
triangulaquè ABD DBC ſunt ęqualia, patet magnitudinis ex v­
triſ〈que〉 triangulis compoſit centrum grauitatis eſſe medium rectæ lineæ
EF; quod eſt punctum H, vt factum furt. Quoniam autem dia­
metri cuiuſlibet parallelogrammi ſeſe bifariam diſpeſcunt, e­
rit punctum H, vbi diametri parallelogrammi ABCD con­
currunt. ergo punctum H, in quo diametri coincidunt; ipſius
ABCD centrum grauitatis exiſtit. quod demonſtrare opor­
rebat.
1
ex 34.pri
mi.
5. post hu­
ius.
4. huius.
52[Figure 52]
SCHOLIVM.
Cognito centro grauitatis cuiuſlibet parallelogrammi,
vult Archimedes oſtendere centrum grauitatis triangulorum.
& quoniam in hac poſtrema demonſtratione aſſumpſit cen­
trum grauitatis trianguli ABD eſſe punctum E, videtur or
dinem peruertiſſe, & per ignotiora doctrinam tradidiſſe; cùm
non ſit adhuc oſtenſum, in quo ſitu dictum centrum in trian­
gulis reperiatur. quod tamen ſi rectè perpendamus, non ita ſe
habet. Nam vis demonſtrationis eſt in hoc conſtituta, vt
ſupponatur triangulum habere centrum grauitatis, idquè tan
ùm eſſe intra ipsum triangulum, quod quidem ſupponi po­
teſt. cùm triangulum ſit figura ad eaſdem partes concaua. ne­
〈que〉 enim refert, ſiuè centrum ſit in E, ſiuè in alio ſitu, dum­
modo intra triangulum exiſtat. demonſtratio enim eodem mo­
do ſemper concludet punctum H centrum eſſe grauitatis pa
rallelogrammi AC, quod idem obſeruandum eſt in nonnullis
alijs demonſtrationibus. vt in ſecunda demonſtratione deci­
mæ tertiæ, hui^{9} & in prima ſecundilibri. Antequam autem Ar­
chimedes centrum grauitatis triangulorum oſtendat, nonnul
las pręmittit propoſitiones.
9. post hu­
ius.
PROPOSITIO. XI.
Si duo triangula inter ſe ſimilia fuerint, & in i­
pſis ſint puncta ad triangula ſimiliter poſita & alre
rum punctum trianguli, in quo eſt, centrum fue­
rit grauitatis, & alterum punctum trianguli, in
quo eſt, centrum grauitatis exiſtet.
1
Dicimus quidem puncta in ſimilibus figuris eſſe
ſimiliter poſita, è quibus ad æquales angulos du­
ctæ rectæ lineæ, æquales efficiunt angulos ad ho­
mologalatera. Vt dictum fuit in ſeptimo poſtulato.
53[Figure 53]
Sint duo triangula ABC DEF ſimilia. ſit què AC ad DE, vt
AB ad DE, & BC ad EF. & in præfatis triangulis ABC DEF
ſint puncta HN ſimiliter poſita ſitquè punctum H centrum grauitatis
trianguli ABC. Dico & punctum N centrum eſſe grauitatis trianguli
DEF. non ſit quidem, ſed, ſi fieripoteſt, ſit punctum G centrum grauita
tis trianguli DEF. connectanturquè HA HB HC, DN EN FN,
DG EG FG. Quoniamigitur ſimile eſt triangulum ABC triangulo
DEF, & ipſorum centra grauitatum ſunt puncta HG. ſimi­
lium autem figurarum centra grauitatum ſunt ſimiliter poſita; ita vt
ab ipſis ad ęquales angulos ductæ rectæ lineę æquales faciant
angulos ad homologa latera, vnum〈que〉mquè vnicuiquè; erit angulus
GDE ipſi HAB aqualis. at verò anguius HAB aqualis est angulo
EDN, cùm ſint puncta HN ſimiliter poſita: angulus igitur EDG
angulo EDN æqualis existit. maior minori quòd fierinon potest. Non
igitur punctum G centrum eſt grauitatis trianguli DEF. Quare eſt
punctum N. quod demonstrare oportebat.
1
6.& 7 poſt
huius.
SCHOLIVM.
In hac propoſitione ſupponit Archimedes dari poſſe pun­
cta in triangulis ſimilib^{9} ſimiliter poſita, qd quidem ſieri poſſe
oſtendimus in ſcholijs ſeptimi poſtulati. Præterea idem vide­
tur Archimedes in triangulis demonſtrare, quod in ſexto po­
ſtulato vniuerſaliter in figuris ſuppoſuit. Nam ſi centra gra­
uitatis ſupponuntur in ſimilibus figuris eſſe ſimiliter poſita;
& in ſimilibus triangulis quo〈que〉 erunt ſimiliter poſita. In­
ter hęc tamen maxima eſt differentia, nam in poſtulato inquit,
centra grauitatum in ſimilibus figuris eſſe ſimiliter poſita; cu
ius quidem conuerſum, nempè puncta in ſimilibus figuris ſi­
militer poſita eſſe ipſarum centra grauitatis, eſt falium. quod
eſt quidem manifeſtum abſ〈que〉 alio exemplo. ac propterea
Archimedes hoc in loco inquit, ſi duo erunt punſta in ſimi­
libus triangulis ſimiliter poſita, & alterum ipſorum fuerit cen­
trum grauitatis. & alterum quo〈que〉 centrum grauitatis exiſtet.
Vnde propoſitio hęc potiùs eſt conuerſa poſtulati, quàm
eadem.
Ob demonſtrationem autem nouiſſe oportet, quòd ſi pun
ctum G fuerit in linea DN, tuncanguli EDG EDN eſſent in
terſe ęquales, ac propterea demonſtratio nihil abſurdi conclu
deret. In hoc autem caſu oſtendendum eſſet, angulum EFG
ipſi EFN ęqualem eſſe, vel FEG ipſi FEN. quæ quidem eo­
dem prorſus modo oſtendentur. comparando nempè angu­
los EFG EFN angulo BCH; angulos verò FEG FEN ipſi
CBH. Quòd ſi G fuerit in alio ſitu, vt in triangulo EDN,
tuncanguli FDG FDN oſtendentur ęquales. & ita in alijs
caſibus, vbicun〈que〉 ſcilicet fuerit punctum G, ſemper ali­
quod inuenietur huiuſmodi abſurdum. quæ quidem omni­
nò fieri non poſſunt.
1
PROPOSITIO. XII.
Si duo triangula ſimilia fuerint, alterius verò
trianguli centrum grauitatis in rectalinea fuerit,
quæ ſit ab aliquo angulo ad dimidiam baſim du­
cta; & alrerius trianguli centrum grauitatis erit in
linea ſimiliter ducta.
54[Figure 54]
Sint duo triangula ABC DEF ſimilia ſitquè AC ad DF, vt
AB ad DE, & BC ad FE. Diuiſaquè AC bifariam in G, iunga
tur BG. centrum verò grauitatis trianguli ABC ſit punctum H in li
nea BG. Dico centrum grauitatis trianguli EDF eſſe in recta linea ſi
militer ducta. ſecetur DF bifariam in puncto M. & iungatur EM.
& vt BG ad BH, ita fiat ME ad EN. connectanturquè AH
HC, DN NF. Quoniam enim eſt BA ad ED, vt AC ad DF, &
AG dimidia eſt ipſius AC; ipſius verò DF dimidiaest DM; erit BA
ad ED, vt AG ad DM. Quoniam autem ob triangulorum
ABC DEF ſimilitudinem angulus BAC angulo EDF eſt ę­
qualis. & vt AB ad DE, ita AG ad DM; permutando〈que〉; AB
AG, vt DE ad DM; erit triangulum ABG triangulo DEM ſimile.
ſimilium ant triangulorum anguli sunt ęquales, et circa æquales angulos late
1ra sut proportionalia. erit
igitur angul^{9} AGB angulo

DME aqualis, et ABG ip
ſi DEM æqualis quare
vt AG ad DM, ita eſt BG
ad EM, & vt AB ad DE,
ita BG ad EM; & pmu­
tado AB ad BG, vt DE
ad EM. eſt autem BG ad
BH, vt ME ad EN, erit igitur ex æquali AB ad BH, vt DE ad EN.
rurſuſquè permutando AB ad DE, vt BH ad EN. quoniam
autem anguli ABH DEN, quos ipſæ lineę continent, ſunt
æquales, erit triangulun. ABH triangulo DEN ſimile. qua
re anguli ſunt inter ſe æquales, & circa a quales angulos latera ſunt
proportionalia ſi autem hoc, angulus BAH angulo EDN est æqualis.
Vnde & reliquus angulus HAC angulo NDF æquolis exiſtit. qui­
dem totius BAC ipſi EDF eſt æqualis. Eademquè ratione an-
gulus BCH ipſi EFN est æqualis. & angulas HCG angulo NFM
æqualis, oſtenſum est autem angulum ABH ipſi DEM aqualem eſſe.
ob ſimilitudinem autem riangulorum ABC DEF totus an
gulus ABC eſtipſi DEF ę ualis: ergo & reliquus angulus HBC
ipſi NEF æqualis exiſtit. Porrò ex his omnibus patet puncta HN ad
homologa latera eſſe ſimiliter poſita, & cum ipſis angulas æquales effi­
cere. Cùm igitur puncta HN ſint ſimiliter poſita; & punctum H cen­
trum eſt grauitatis trianguli ABC, & puncium N trianguli DEF cen­
trum grauitatis existet. exiſtente igitur centro grauitatis H in li
nea BG ab angulo ad dimidiam baſim ducta. & alterum gra
uitatis centrum N in linea EM ſimiliter ducta reperitur.
quod demonſtrare oportebat.
16. quinti.
6.ſeati.
16. quinti.
22. quinti.
16. quinti.
6. ſexti.
7. post hu
ius.
11.huius.
55[Figure 55]
SCHOLIVM.
In ſe〈que〉nti Archimedes oſtendet, in qua linea reperitur cem
trum grauitatis cuiuſlibet trianguli. quod quidem duobus aſ­
ſequitur medijs. Diligenter autem omnia ſunt conſideranda;
quoniam in hoc conſiſtit tota perſcrutatio centri grauitatis
triangulorum. Quapropter vt prior demonſtratio appareat
perſpicua, hęc antea demonſtrabimus.
1
LEMMA. I.
Æquidiſtantes lineæ lineas in eadem proportione diſpe­
ſcunt.
Sintlineę AB CD, quas ſecent æqui­

diſtantes lineæ AC EF BD. Dico ita eſ­
ſe BE ad EA, vt DF ad FC. primùm
quidem AB CD vel ſunt
vel minùs. ſi ſunt æquidiſtantes, iam habe
tur intentum. Nam BE erit æqualis DF,
& EA ipſi FC. vnde ſequitur ita eſſe BE

ad EA, vt DF ad FC.
34. primi.
56[Figure 56] 57[Figure 57]
Si verò AB CD non fuerint æquidi­
ſtantes, concurrant in G, vt in ſecunda fi­

gura, & quoniam BD EF æquidi­
ſtantes, erit GB ad BE, vt GD ad
& componendo GE ad EB, vt GF ad
conuertendoquè BE ad EG, vt DF ad
FG, rurſus quoniam EF AC ſunt æquidi
ſtantes; erit GE ad EA, vt GF ad FC, e­
ritigitur ex æquali BE ad EA, vt DF ad FC.
2.ſexti.
18.quinti.
cor.4.quinti
58[Figure 58]
Secent verò ſeſe lineæ AB CD, vt in tertia figura, ſimi­
litudinem triangulorum BGD EGF, it a erit BG ad GE,
DG ad GF. & componendo BE ad EG, vt DF ad FG.
verò GE ad EA, vt GF ad FC. ergo ex æquali BE ad EA
erit, vt DF ad FC. quod demonſtrare oportebat.
1
ex 4. ſexti.
18. quinti.
2. ſexti.
LEMMA. II.
Sit A ad B, vt C ad D; rurſus A ad E ſit, vt C ad F.
Dico primùm A ad BE ſimul ita eſſe, vt C ad DF.
59[Figure 59]
Quoniam enim A eſt ad B, vt C ad D, erit conuertendo
B ad A, vt D ad C. eſt autem A ad E, vt C ad F; ergo ex ę­
 quali B erit ad E, vt D ad F. quare componendo BE ad
E, vt DF ad F. quoniam autem A eſt ad E, vt C ad F; e
rit conuertendo E ad A, vt F ad C. rurſus igitur ex ęquali
erit BE ad A, vt DF ad C. ac deni〈que〉 conuertendo A e­
rit ad BE, vt C ad DF.
cor.4.quinti
22. quinti.
18. qninti.
cor.4.quinti
22. quinti.
Si verò fuerint quattuor magnitudines; vt adhue A (in ea­
dem figura) ad G ſit, vt C ad H. ſimili­

ter oſtendetur A ad omnes BEG ſimul
ſumptas ita eſſe, vt C ad omnes ſimul
DFH. ſumendo vt in ſecunda figura BE
pro vna tan ùm magnitudine, & DF pro
alia; erunt〈que〉 ex vtra〈que〉 parte tres tantùm
magnitudines; eritquè A ad BE ſimul,
vt C ad DF ſimul, vt oſtenſum eſt, dein
de A ad G eſt, vt C ad H, erit igitur
A ad BEG ſimul, vt C ad DFH.
1 60[Figure 60]
Pariquè ratione ſi quin〈que〉 fuerint magnitudines, eodem
modo tres mediæ iungatur ſimul, ita vttres ſint duntaxat magni
tudines. & ſic in infinitum. quod demonſtrare oportebat.
COROLLARIVM.
Ex hoc elici poteſt. quòd ſi fuerint quotcun〈que〉 magnitudi
nes proportionales; & alię ipſis numero æquales, & in eadem
proportione, vt ſcilicet ſit (vt in prima figura) A ad B, vt C
ad D, B verò ad E, vt D ad F. deinde vt E ad G, ſic F
ad H, & ita deinceps, ſi plures fuerint magnitudines, ſi­
militer erit A ad omnes BEG ſimul ſumptas, vt C ad om­
nes ſimul DFH.
Primùm quidem A eſt ad B, vt C ad D. & quoniam ma
gnitudines ſunt proportionales, ex ęquali erit A ad E, vt
ad F. ſimiliter A ad G, vt C ad H. Ex quibus ſequitur
A ad BE ſimul ita eſſe, vt C ad DF. A verò ad omnes
BEG ſimul, vt C ad omnes ſimul DFH. & ita ſi plures fue
rint magnitudines.
22. quinti.
LEMMA. III.
Sit triangulum ABC, cuiuslatus BC in quotcun〈que〉 di­
uidatur partes æquales BE ED DF FC. & a punctis EDF
ipſi AB equidiſtanres ducantur EG DH FK. rurſus à pun
ctis GHK ipſi BC ęquidiſtantes ducantur GL HM KN.
Dico triangulum ABC ad omnia triangula ALG GMH
HNK KFC ſimulſumpta eandem habere proportionem,
quam habet CA ad AG.
1
Quoniam enim FK ęquidiſtans eſtipſi DH; erit CF ad FD,
vt CK ad KH. ſunt〈que〉 CF FD æquales; ergo & CK KH in­
terſe ſunt æquales. ſimiliter propter lineas æquidiſtantes FK
DH EG, ita eſt KH ad HG, vt FD ad DE; eſt autem FD
æqualis DE; erit igitur KH ipſi HG æqualis. Pariquè ra­

tione oſtendetur ob ęquidiſtantes lineas DH EG BA, lineam
HG ipſi GA æqualem eſſe. Ex quibus patet CK KH HG
GA inter ſe æquales eſſe. Quoniam autem trianguloru ABC
kFC angulus ad C eſt vtri〈que〉 communis; & ABC ipſi kFC,
& BAC ipſi FKC æqualis, cum ſit Fk ipſi AB æquidiſtans;
erit triangulum ABC ipſi KFC ſimile. & quonian NK FC,
& HN KF ſunt ęquidiſtantes, erunt anguli KCFCkF angu
lis HkN KHN ęquales; ac propterea reliquus CFK reliquo
KNH ęqualis: latus verò CK lateri KH eſt ęquale; erit igi­
 tur triangulum KFC triangulo HNK ſimile, & ęquale. ſimi
literquè oſtendetur omnia triangula ALG GMH HNK KFC
interſeſe ſimilia, & æqualia eſſe. & obid ipſi ABC ſimilia eſſe.
Fiat igit vt AC ad AG, ita AG ad alia O. ſimiliterv AC ad GH,
ita GH ad P. rurſusvt AC ad Hk, ita HK ad 〈que〉 deniquè
vt AC ad Ck, ita CK ad R. & quoniam AG GH HK KC
ſunt æquales, eadem AC ad vnamquam〈que〉 ipſarum ean­
dem habebit proportionem, ergo eandem quo〈que〉 habebit
propoſitionem AG ad O, vt GH ad P, & HK ad Q, &
1KC ad R. ac propterea lineæ OPQR inter ſe ſunt æquales.
Atverò quoniam ita eſt AC ad AG, vt AG ad O, & vt
AC ad GH, ita GH, hoc eſt AG ipſi ęqualis, ad P. rurſus
vt AC ad HK, ita HK, hoc eſt AG ad 〈que〉 ac tandem vt
AC ad KC, ita KC, hoc eſt AG ipſi ęqualis, ad R. erit
ad omnes conſe〈que〉ntes ſimul ſumptas AG GH HK KC,
hoc eſt erit AC ad eandem AC, vt AG ad omnes ſimul
OPQR. vnde ſequitur omnes ſimul OPQR ipſi AG ęqua
les eſſe. Ita〈que〉 quoniam ſimilia triangula in dupla pro­
portione laterum homologorum, erit triangulum ABC ad
ALG, vt AC ad O. eodemquè modo erit triangulum ABC
ad GMH, vt AC ad P. rurſus ABC ad HNK, vt AC ad
Q, & vt idem ABC ad KFC, ita AC ad R. triangulum
igitur ABC ad omnes conſe〈que〉ntes, videlicet ad omnia triam
gula ſimul ſumpta ALG GMH HNK KFC, eritvt AC ad
omnes ſimul OPQR. hoc eſt ad AG. oſtenſum eſt igitur,
quod propoſitum fuit.
2. ſexti.
1. lemma.
29. primi.
76. primi.
ex 17 quini.
ex præcedem
ti lemmate
19.ſexti.
ex præcedem
ti lemmate
61[Figure 61]
PROPOSITIO. XIII.
Omnis trianguli centrum grauitatis eſt in recta
linea ab angulo ad dimidiam baſim ducta.
Sit triangulum ABC. & in ipſo ſit AD ab angulo A ad dimi­
diambaſim BC ducta. oſtendendum est, centrum grauitatis trianguli
ABC eſſe in linea AD. Non ſit quidem, ſed ſi fieri potest ſit punctum
H. & ab ipſo ducatur HI æquidiſtansipſi BC, quæ ipſam AD
in I. Deinde diuiſa DC bifariam, idquè ſemper fiat, dones relinqua­
tur linea Dω minor ipſa HI. Diuidaturquè ipſarum vtra〈que〉 BD DC
in partes æquales Dω; parteſquè in DC exrſtentes ſint Dω ωβ
βZ ZC; quibus reſpondeant æquales partes DααζζO OB. &
a ſectionum punctis ducantur OE ζG αL ωM βK ZF æquidictan
tes ipſi AD. & connectantur EF Gk LM quæ nimirum ipſi BC
æquidistantes erunt. cùm enim ſint BD DC interſe equales, iti­
dem OB ZC æquales; erit DO ipſi DZ ęqualis. quare DO
ad OB eſt, vt DZ ad ZC. Quoniam autem EO FZ ſunt
1ipsi AD æquidiſtantes, erit AE ad EB, vt DO ad OB; & vt
DZ ad ZC, ſic AF ad FC. at〈que〉 DO ad OB eſt, vt DZ ad
ZC. erit igitur AE ad EB, vt AF ad FC. quare EF ipſi BC
eſt æquidiſtans, eodemquè modo oſtendetur, ita eſſe AG ad

GB, vt AK ad KC, & AL ad LB, vt AM ad MC. ex quib^{9}
ſequitur LM GK EF non ſolùm ipſi BC, verùm etiam inter­
ſeſe parallelas eſſe. ſecct EF lineas Gζ Kβ in Xε. ipſam verò
AD in T. lineaquè GK ſecet Lα Mω in Nδ, & AD in Y.
linea deniquè LM ipſam AD in S diſpeſcat. Quoniam au
tem Dω eſt ipſi HI æquidiſtans, eſtquè Dω minor quam HI, li
nea ωM ipſi AL ęquidiſtans ipſam HI ſecabir. ac propterea
punctum H centrum grauitatis trianguli ABC extra paral­
 lelogrammum DM reperitur. At verò quoniam LD DM
ſunt para lelogramma, erunt LS αD inter ſe æquales, ſimili­
ter SM Dω ęquales. ſuntverò αD Dω ęquales: ergo & LS
SM inter ſe ſunt ęquales. eademquè rarione NY Yδ inter ſe­
ſe, & ipſis LS SM ęquales exiſtent. quarelinea SY bifariam
diuiditlatera oppoſita parallelogrammi MN. pariquè ratio­
ne oſtendetur lineam YT bifariam diuidere oppoſita latera
parallelogrammi KX; lineamquè TD latera oppoſita
1lelogrammi FO bifariam quo〈que〉 diuidere. Ita〈que〉 parallelogrà
mi MN centrum grauitatis est in linea ΥS. parallilogrammi ver
KX grouitatis centrum est in linea TΥ. parallelogrammi autem FO in
linea TD; magnitudinis igitur ex his omnibus parallelogrammi
MN KX FO compoſitæ centrum grauitatis eſt in recta linea S D. ſiv
ita〈que〉 punctum R. quod quidem erit centrum grauitatis figura
LNGXEOZF εKδM. lungatur〈que〉; RH, & producatur, quæ ipsa ωM
ſecet in P. ipſiquè AD a puncto C æqui diſtans ducatur CV, qu
ipſi RH occurrat in V. triangulum ita〈que〉 ADC ad omnia triangu
la ex AM MK kF FC deſcripta ſimiliaipſi ADC, hoc eſt ad tria
gula ASM M δK KεF FZC ſimul ſumpta eandem habet propor
tionem, quam habet CA ad AM. ſiquidem ſunt AM MK kF FC
æquales quia verò & triangulum ADB ad omnia ex AL LG GE
EB deſcripta triangula ſimilia ALS LGN GEX EFO eandem ha
bet proportionem, quam ‘BA ad AL: & antecedentes ſimul
omnes conſe〈que〉ntes, hoc eſt totum triangulum ABC ad on
nia triangula ſimul ſumpta, quæ ſunt in AB, & in AC conſti­
tuta, eandem habebit proportionem, quam habet AC AB ſi
mul ad AM AL ſimul, quia verò ob ſimilitudinem triangulorum
ABC ALM CA ad AM eſt, vt BA ad AL; erit CA ad AM, vt
CA BA ſimul ad AM AL ſimul. triangulum igitur ABC ad omnia
prædicta triangula eandem habet proportionem quam habet CA ad AM.
At〈que〉 CA ad AM maiorem habet proportionem quàm VR ad RH; e­
tenim proportio ipſius CA ad AM eſt eadem, quæ est totius VR adipsam
R. p. quandoquidem triangula ACD MCω ſunt ſimilia. ſint〈que〉; AD &
Mω ęquidiſtantes, ſitquè propterea CA ad AM, vt CD ad
Dω. & quoniam VR DC àlineis DR ωp CV
diuiduntur; erit Cω ad ωD, vt VP ad PR. & componendo
ad Dω, vt VR ad RP. quare vt CA ad AM, ita VR ad
quia verò VR ad RP maiorem habet proportionem,
ad RH. maiorem quo〈que〉 habebit proportionem CA ad
AM, quàm VR ad RH. eſt autem CA ad AM, vt triangulum
ABC ad omnia triangula in lineis AC AB. (vt dictum eſt)
conſtituta; ergo & triangulum ABC adprædicta triangula maio
rem habet proportionem, quàm VR ad RH. Quare & diuidendo pa-
rallelogramma MN kX FO hoc eſt figura LNGXEOZF εK δM) ad
circumrelicta triangula in lineis AC AB conſtituta maiorem ha-
1bent proportionem, quam NH ad HR. linea igitur, quæ eandem
habeat proportionem ad HR, quam parallelogramma MN
kX FO ad circumrelicta triangula, maior erit, quàm VH
Fiat itaquè in eademproportione QH ad HR, ut parallelogramma ad
triangula; erit vti〈que〉 QH maior, quam VH. Quoniam igitur eſt
magnitudo ABC, cuius centrum grauitatis est H, & ab ea magnitudo

auferatur compoſita ex MN kX FO parallelogrammis; & magnitudi
nis ablatæ centrum grauitatis eſt punctum R; magnitudinis reliquæ ex
circumrelictis triangulis compoſitæ centrum grauitatis erit in recta li-
nea RH ex parte H producta, aſſumptaquè aliqua vt, QH, quæ ad
HR eam habeat proportionem, quam habet magnnudo ex parallelo­
grammis MN KX FO conſtans ad reliquum, hoc eſt ad reli­
qua triangula, ergo punctum Q centrum est grauitatis magnitudinis
ex ipſis circumrelictis triangulis compoſitæ. quoa fieri non poteſi aucta
enim recta linea θκ per Q ipſi AD æquidistante in eodem plano triam
guli ABC, in ipſa eſſent omnia centra grauitatis trian­
gulorum, hoc est in vtram〈que〉 partem Qθ Qκ, centraquè
grauitatis trianguli ALM, ac centrum magnitudinis ex vtriſ­
què triangulis LGN MK δ compoſitę in parte Qθ eſſe deberent.
1centra verò grauitatis magnitudinis ex GEX KεF compo­
ſitę, ac magnitudinis ex. EBO FZC compoſſtæ, eſſent in par
te Qκ, ita vt punctum Q magnitudinis ex omnibus trian­
gulis compoſitæ centrum eſſet grauitatis. quæ quidenſunt om­
nino abſurda. Quòd ſi ducta linea per Q, non fuerit etiam
ipſi AD ęquidiſtans, eadem ſe〈que〉ntur in conuenientia. Ma
niſestum eſt igitur; quod propoſitum fuerat.
ex t. deci­
mi.
2. ſexti.
2. ſexti.
34. primi.
3. lemma.
ex12.quinti
ex12.quinti
ex 4.ſexti
1. lemma.
8. quinti.
11. quinti.
8. quinti.
20. quinti
add.
8.huius.
62[Figure 62] 63[Figure 63]
SCHOLIVM.
Id ipſum vult ad huc Archimedes aliter oſtendere. ob ſe〈que〉m
tem verò demonſtrationem hoc priùs cognoſcere oportet.
LEMMA.
Si intra triangulum vni lateri ęquidiſtans ducatur, ab op­
poſito autem angulo intra triangulum quoquè recta ducatur
linea, æquidiſtantes lineas in eadem proportione diſpeſcet.
Hoc in ſecundo noſtrorum planiſphęriorum libro in ea
parte oſtendimus, vbi quomodo conficienda ſit ellipſis, inſtru
mento à nobis inuento demonſtrauimus. hoc nempè modo,

Sit triangulum ABC, ipſiquè BC in­
tra triangulum ducatur vtcumquè æ­
quidiſtans DE. à punctoquè A intra
triangulum ſimiliter quocum〈que〉 du­
catur AF; quæ lineam BC ſecet in F;
lineam verò DE in G. Dico ita oſſe
CF ad FB, vt EG ad GD. Quoniam
enim GE FC ſunt æquidiſtantes, erit
triangulum AFC triangulo AGE æquiangulum, vt
AF ad AG, ita CF ad EG. ob eandemquè cauíam ita eſt FA
ad AG, vt FB ad GD. quare vt CF ad EG, ita eſt FB ad
ac permutando, vt CF ad FB, ita EG ad GD. quod
ſtrare oportebat.
1
ex 4.ſexti
11.quinti.
16.quinti.
64[Figure 64]
IDEM ALITER.
Sit triangulum ABC, ducaturquè AD ab angulo A ad dimidiam
baſim BC. Dico in linea AD centrum eſſe grauitatis trianguli ABC.
N on ſit autem, ſed ſi fieri poteſt; ſit H. iunganturquè AH HB HC, &
ED DF FE ad dimidias BA BC AC ducantur, ſecetquè EF ip­
ſam AD in M. & ipſi AH æquidistantes ducantur EK FL. &

iungantur KL LD Dk DH; ſecetquè DH ipſam KL in N.
iungaturquè MN. Quoniam igitur triangulum ABC ſimile est triam
gulo DFC, cùm ſit BA ipſi FD æquidistans; ſiquidem ſunt late­
 ra CA CB bifariam diuiſa, ideoquè ſit CF ad FA, vt CD
ad DB. trianguliquè ABC centrum grauitatis est punctum H; &
trianguli FDC centrum grauitatis erit punctum L. puncta enim HB
intra vtrumquè triangulum ſunt ſimiliter poſita. etenim ad homologa
latera angulos efficiunt æquales. hoc enim perſpicuum. est cùm enim
ſint triangulorum ABC DFC homologa latera AC FC,
AB FD, BC DC, ſintquè AH FL æquidiſtantes; erit an­
gulus LFC angulo HAC ęqualis. ſed angulus CFD eſt ipſi
1CAB æqualis; reliquus igitur angulus LFD reliquo HAB
æqualis exiſtit. & quoniam ita eſt CF ad FA, vt CL ad
cùm ſint FL AH ęquidiſtantes. CF verò dimidia eſt ipſius
CA, erit & CL ipſius quo〈que〉 CH dimidia. at CD ipſius
CB dimidia exiſtit; erit igitur DL ipſi BH ęquidiſtans.
propterea angulus LDC eſt ipſi HBC ęqualis, & LDF
HBA ęqualis. cùm ſittotus CDF toti CBA ęqualis; anguli
verò ACH & HCB tam ſunt trianguli ABC, quàm FDC.
Obeandem autem rationem trianguli EBD centrum grauitatis est pun-
ctum K. ſimiliter enim oſtendetur punctum K in triangu­
lo EBD eſſe ſimiliter poſitum, vt H in triangulo ABC.
Quare magnitudinis ex vtriſquè triangulis EBD FDC compoſitæ
centrum grauitatis eſt in medietate lineæ kL. cum triangula EBD
FDC ſint æqualia. ſunt enim in ęqualibus baſibus BD
& in ijſdem parallelis EF BC, ſiquidem eſt AE ad EB,
AF ad FC. quippè cùm latera AB AC ſint bifariam diui­
ſa. medium veròipſius kL eſt punctum N; cùm ſit KE ipſi AH
ęquidiſtans, & ob id ſit BE ad EA, vt Bk ad kH. & vt
ad EA, ita CF ad FA; vt autem CF ad FA, ſic CL ad LH.
quare vt BK ad KH, ita CL ad LH. Si autem hoc. æquidi-
ſtans est BC ipſi kL, & iuncta est DH, erit igitur BD ad DC, vt
KN ad NL. D verò medium eſt ipſius BC. ergo & me­
dium eſt ipſius KL. Quare magnitudinis ex vtriſquè dictorum trian
gulorum EBD & FDC compoſitæ centrum grauitatis est punctum
N. parallelogrammi verò AEDF centrum grauitatis eſt punctum M,
vbi ſimiliter diametri concurrunt, ac propterea magnitudinis ex
omnibus triangulis EBD FDC vna cum parallelogramo AEDF
compoſitæ centrum grauitatis eſt in linea MN. Verùm triangulorum
EBD FDC, ſimulquè parallelogrammi AEDF, hoc eſt totius
trianguli ABC grauitatis centrum est punctum H; linea igitur MN pro
ducta tranſibit per punctum H. quod eſſe non poteſt. etenim cùm ſit
KN ipſi BD æquidiſtans; erit BK ad KH, vt DN ad
NH: vt autem BK ad KH, ita eſt BE ad EA, & vt BE ad
EA, ita eſt DM ad MA, cùm ſit EM ipſi BD æquidiſtans.
erit igitur DM ad MA, vt DN ad NH. quare MN ipſi AH
eſt ęquidiſtans; ideoquè MN numquam cùm AH conueni­
re poteſt. Non est igitur punctum H centrum grauitatis trianguli
1ABC. quare non eſt extra lineam AD. in ipſi igitur exiſtit. Quod
demonitrare oportebat.
2.ſexti.
11.huius.
29. primi.
2. ſexti.
2.ſexti.
29. primi.
11. huius.
4.huius.
38. primi.
2.ſexti.
2.ſexti.
11.quinti.
2.ſexti.
lemma.
*
11.huius.
*
A
65[Figure 65]
SCHOLIVM.
Inquit Archimedes linea igitur MN producta tranſibit per pun­
ctum H. quod eſſe non poteſt, nempè, vt non ipſamet linea MN,
ſed eius pars, ſiuead M, ſiue ad N producta cum H conue
nireoporteat. cùm tamen ipſamet linea MN per punctum
H tranſire debeat. ita vt punctum H ſit inter puncta MN;
hoc eſt in linea MN, & non in eius parte producta. Nam ſi
punctum H centrum eſt grauitatis totius trianguli ABC.
punctum verò N centrum grauitatis magnitudinis ex triangu
lis EBD FDC compoſitę; at〈que〉 punctum M centrum gra­
uitatis parallelogrammi AEDF; oportet vt punctum H ita li­
neam diuidat MN; vt eius partes magnitudinibus permuta­
tim reſpondeant. vt nimirum pars ad M ad partem ad N ſit,
vt magnitudo ex triangulis EBD FDC conſtans ad parallelo
grammum AEDF. vt ex ſexta, & octaua huius propoſitione
perſpicuum eſt. Quare punctum H in linea MN eſſe debe­
ret; vt ipſemet Atchimedes paulò ſuperiùs affirmauit; cùm in­
 quit. ac propterea magnitudinis ex omnibus compoſitæ contrum grauita­
tis eſt in linea MN. & non dixit in eius parte producta. Quodiv
ca vel deldum eſt verbum illud producta, tanquam ab aliquo
additum, vel ideo tamen hoc dixiſſe voluit Archimedes, vt o­
ſtenderet lineam MN nullo modo (etiam ſi produceretur) cum
H conuenire poſſe.
A
*
PROPOSITIO. XIIII.
Omnis trianguli centrum grauitatis eſt punctum
in quo rectæ lineæ ab angulis trianguli ad dimidia
later a ductæ concurrunt.
1
Sit triangulum ABC, & ab angulo A ducatur AD ad dimi­
diam BC. BE verò ab angulo B ad dimidiam AC. quę quidem
lineę AD BE ſeinuicem ſecent in pum

cto H. Quoniam igitur centrum grauita­
tis trianguli ABC est in vtra〈que〉 linea
AD BE; hoc enim demonstratum eſt in
pręcedenti. erit vti〈que〉 centrum graui­
tatis, vbilineç AD BE ſe inuicem ſecant.
ſecant verò ſeſe in H. ergo punctum
H centrum eſt grauitatis trianguli ABC.
quod demonſtrare oportebat.
66[Figure 66]
SCHOLIVM.
Similiter ſi ducta fuerit CH, & producta, bifariam ſecaret
AB. In hac enim linea eſſet centrum grauitatis trianguli; cem
trum verò eſt in linea ab angulo ad dimidiam baſim ducta:
ergo hæc linea ab angulo C ad dimidiam AB ducta eſſet.
Præterea ſi linea à puncto C ad dimidiam AB ducta non tran
ſiret per H; eſſet vti〈que〉 in hac linea centrum grauitatis; cen­
trum quo〈que〉 grauitatis eſt in linea AD, & in linea BE, ut in
H; vnius igitur figurę plura darentur centra grauitatis. quod
fieri non poteſt. quod quidem, cùm ſit in con ueniens, nos in
noſtro Mechanicorum libro dari non poſſe ſuppoſuimus.
Quare linea CH indirectum ducta, bifariam ſecaret AB.
quod quidem paulò infra aliter quo〈que〉 oſtendemus, nonnul
lis prius demonſtratis; quæ Archimedes ob ſe〈que〉ntem demon­
ſtrationem, tanquam demonſtrata ſupponit. Vult enim Ar­
chimedes, poſtquam inuenit centrum grauitatis cuiuſlibet
trianguli, centrum quo〈que〉 grauitatis quærere trapetij duo la­
tera ęquidiſtantia habentis. quod eſt quidem pars trianguli,
& tanquam fruſtum a triangulo abſciſſum. ſupponitquè den
trum grauitatis cuiuſlibet trianguli eſſe in recta linea baſi du
cta ęquidiſtante, quæ latera ita diuidat, vt partes ad uerticem
ſint reliquarum partium duplæ. quod quidem ortum ducit
ex cognitione alterius theorematis oſtendentis centrum
1uitatis cuiuſlibet trianguli eſſe in recta linea ab angulo ad di­
midiam baſim ducta (vt Archimedes demonſtrauit) & inſu­
per in eo puncto, quod dictam lineam diuidatita, vt pars ad
angulum reliquę ad baſim ſit dupla. Quare hoc prius ita oſtem
demus.
13.huius.
PROPOSITIO.
Omnis trianguli centrum grauitatis eſt punctum in recta
linea ab angulo ad dimidiam baſim ducta exiſtens, quod li­
neam diuidat, ita vt poitio ad angulum reliquæ ad baſim, ſit
dupla.
Sit triangulum ABC, in quo ab an

gulo A ad dimidiam baſim BC re­
cta ducatur linea AD. Ducaturquè
ab angulo B ad dimidiom baſim
AC linea BE, quæſecet AD in F. Et
quoniam centrum grauitatis triangu­
 li ABC eſt punctum F; oſtendendum
eſt lineam FA ipſius FD duplam eſ­
ſe. iungatur FC. quoniam enim AE
eſt equalis ipſi EC, erit triangulum
ABE triangulo EBC æquale, cùm
ſint ſub eadem altitudine. Ob eandemquè cauſam triangulum
AFE triangulo EFC exiſtit æquale. ſi igitur à triangulo ABE
auferatur triangulum AFE, & à triangulo EBC triangulum
auferatur EFC; relin〈que〉tur triangulum ABF triangulo BFC
æquale. Rurſus quoniam BD eſt æqualis ipſi DC; erit trian­
 gulum BFD triangulo DFC æquale, ſiquidem candem ha­
bentaltitudinem. duplum igitur eſt triangulum BFC triangu­
li BFD. Quare & triangulum ABF trianguli BFD duplum
exiſtit. quia verò triangula ABF FBD in eadem ſunt altitudi
ne, idcirco ſeſe habebunt, vt baſes AF FD. at〈que〉 triangulum
ABF. duplum eſt ipſius FBD; ergo portio AF ipſius FD dupla
exiſtit. quod demonſtrare oportebat.
1
14.huius.
1.ſexti.
1.ſexti.
1.ſexti.
67[Figure 67]
ALITER.
Sit rurſus triangulum ABC, & AD BE ab angulis ad di
midias baſes ductæ ſint erit vti〈que〉 punctum, F (vbi ſe in
cen fecant) centrum grauitatis triangulb ABC. Drco AF a­
pſius FD duplam eſſe. Iungatur DE. Quoniam enim BC

AC in punctis DE bifariam ſecantur; erit
CD ad DB, vt CE ad EA. linea igitur
DE ipſi AB eſt æquidiſtans. trian­
gulum ABC ſimile eſt triangulo
ac propterea ita eſt BC ad CD, vt AB
ad DE. eſt autem. BC dupla ipſius CD
(ſiquidem punctum D bifariam diuidit
BC) erit igitur AB dupla ipſius DE. At
vero quoniam AB DE ſunt parallelæ, erit triangulum AFB
triangulo EFD ſimile. & vt AB ad ED, ita AF ad FD,
autem AB ipſius ED dupla, ergo AF ipſius FD dupla
exiſtit. quod demonſtrare oportebat.
14. huius.
2. ſexti.
4. ſexti.
4.ſexti.
68[Figure 68]
Exijs, quæ demonſtrata ſunt, oſtendemus, quod paulò an
te propoiuimus, nempè cùm lineæ AD BE bifariam ſecent
BC CA. Dico lineam CF productam bifariam quo〈que〉 ſe­
care ipſam AB.
Producatur enim (ijsdem poſitis) CFGH; quæ lineam

AB ſecet in G. & à puncto B
ipſi AD æquidiſtans ducatur
BH. quæ ipſi CG occuriat in
H. Quoniam igitur FD, eſt i­
pſi BH ęquidiſtans, erit CD
ad DB, vt CF ad FH. ve­
rò eſt æqualis BD; ergo CF ipſi
FH æqualis exiſtit. ac propterea
CH dupla eſt ipſius (F. At ve­
rò quoniam ob ſimilitudinem
triangulorum CBH CDF, ita eſt
HC ad CF, vt BH ad DF; erit & BH ipſius FD duplex.
1verùm & AF (ex proximè demonſtratis) ipſius FD duplex
exiſtit. erunt igitur BH FA inter ſe ęquales. Quoniam autem
BH eſt ęquidiſtans ipſi AF, æquiangula erunt triagula GBH
GAF. quare vt BH ad AF, ita BG ad GA, quia verò BH eſt
ipſi AF æqualis; erit & BG ipſi GA æqualis. ergo recta li­
nea EFG bifariam diuidit AB. quod demonſtrare oporte­
bat.
2. ſexti.
ex 4.ſexti
69[Figure 69]
Reliquum eſt, vt ob ſe〈que〉ntem demonſtrationem alteram
propoſitionem oſtendamus.
PROPOSITIO.
Centrum grauitatis cuiuſlibet trianguli eſt in recta linea
baſi ducta æquidiſtante, quæ latus ita diuidat, vt pars ad an­
gulum reliquæ ad baſim ſit dupla.
In trianagulo enim ABC ducta
ſit DE baſi BC æquidiſtans, quæ

latus AB diuidat in D, ita vt DA
ipſius DB ſit duplex. Dico in linea
DE centrum eſſe grauitatis triangu
li ABC. Ducatur ab angulo A ad
dimidiam BC linea AF, quæ di­
 uidat DE in G. erit AD ad DB,
vt AG ad GF, ac propterea erit
AG ipſius GF dupla. punctum er
go G centrum eſt grauitatis trian­
guli ABC. Quare conſtat centrum
eſſe in linea DE. quod demonſtra­
re oportebat
1
2. ſexti.
70[Figure 70]
COROLLARIVM.
Ex hoc elici poteſt centrum grauitatis cuiuſlibet trianguli
eſſe in medio ductæ lineæ baſi æquidiſtantis, quę latus diui­
datita, vt portio ad verticem ſit reliquę ad baſim dupla.
Eſt enim DG ad GE, vt BF ad FC. ſunt verò BF æ­
quales; ergo & DG GE inter ſe ſunt æquales. quare grauita­
tis centrum G eſt medium lineę DE.
lemm.
2. der
ſtratic
13.hi
PROPOSITIO. XV.
Omnis trapezij duo latera inuicem habentis æ­
quidiſtantia centrum grauitatis eſt in recta linea,
quæ latera æquidiſtantia bifariam ſecta coniungit;
ita diuiſa, vt ipſius portio terminum habens mino
rem parallelam bifariam diuiſam ad reliquam por­
tionem eandem habeat proportionem, quam ha
bet vtra〈que〉 ſimul, quæ ſit æqualis duplæ maioris
parallelarum cum minore ad duplam minoris cum
maiore.
Sit trapezium ABCD habens latera AD BC parallela. linea
verò EF bifariam diuidat AD BC. Quòd igitur in linea EF ſit cen
trum grauitatis trapezii, perſpicuum est. productis enim CDG FEG
BAG, li〈que〉t in idem punctum, putà G concurrere. propterea quòd
cùm ſit AD æquidiſtans ipſi BC, neceſſe eſt
ipſius BA ad AG, ipſiusquè FE ad EG, & CD ad DG, quæ ni­
mirum in omnibus eadem eſt, in vnum & idem punctum terminare. erit〈que〉;
trianguli GBC centrum grauitatis in linea GF. ſimiliter〈que〉 trianguli
1 AG D centrum grauitatis in linea EG. ergo reliqui trapezii ABC
centrum grauitatis erit in linea EF. iungatur ita〈que〉 BD, quæ int
æqua in punctis KH diuidatur. ac per ea ducantur LHM NkT
BC æquidiſtantes; quæ lineam EF in punctis RS diſpeſcant
lungantur〈que〉 DF BE, ſecetquè DF lineam LM in X. ip
verò EB ſecet NT in O. Iungaturquè OX, quæ lineam EF

P ſecet. erit ita〈que〉 trianguli DBC centrum grauitatis in linea H
cùm ſit HB tertia pars ipſius B D; ſitquè propterea DH ipſi
HB dupla. & per punctum H ducta ſit baſi BC æquidiſtans M
eſt autem centrum quo〈que〉 grauitatis trianguli DBC in linea DF; q
eſt ab angulo D ad dimidiam BC ducta. Quare dicti triang
centrum grauitatis est punctum X. Eademquè ratione cùm ſit D
tertia pars ipſius DB, ac proptcrea ſit BK ipſius KD dup
ſitquè KN æquidiſtans ipſi AD; erit centrum grauitatis tri
guli ABD in linea KN; idem verò centrum reperitur quo
in linea BE, cùm ſit ab angulo B ad dimidiam AD duc
ergo punctum O, vbi ſe inuicem ſecant, centrum eſt grauitatist
guli ABD. magnitudinis igitur ex vtriſ〈que〉 triangulis ABD BI
compoſitæ, quæ eſt trapezium ABCD, centrum grauitatis est in rect
1nea OX. dicti autem trapezii centrum gauitatis est etiam in li­
nea EF, quare trapezii ABCD centrum grauitatis est punctum
P. At verò triangulum BCD ad ABD proportionem habet eam,
OP ad PX. cùm ſint puncta OX triangulorum centla graui
tatis, ac punctum P vtrorum〈que〉 commune centrum. Sed vt
triangulum BDC adtriangulum ABD, ita eſt quo〈que〉 baſis BC
ad baſim AD. cùm triangula eandem habeant altitudinem,
ſiquidem ſunt in ijsdem parallelis AD BC. quare vt BC ad
AD, ita OP ad PX. Sed quoniam anguli RPO SPX ver­
ticem ſunt ęquales, & angulus PRO ipſi PSX, veluti
ROP angulo PXS eſt ęqualis, erit triangulum OPR triangu
lo XPS ſimile; quare vt OP ad PX, ſic PR ad PS. eſt
BC ad AD, vt OP ad PX; vt igitur BC ad AD, ita RP ad PS.
& antecedentium dupla, duæ ſcilicet BC ad AD, vt duæ PR
ad PS. & componendo duæ BC cum AD ad AD; vt
PR cum PS ad PS. & ad conſe〈que〉ntium dupla, vt ſcilicet
duæ BC cum AD ad duas AD, ita duæ PR cum PS ad duas
PS. dictum eſt autem BC ad AD ita eſſe, vt PR ad PS. quare
conuerrendo AD ad BC erit, vt PS ad PR. &
dupla. hoc eſt duæ AD ad BC, vt duæ PS ad PR. Ita〈que〉 in
eadem ſunt proportione duç BC cum AD ad duas AD, vt
duę PR cum PS ad duas PS. ſicut verò duę AD ad BC, ita duę
PS ad PR. antecedentes igitur ad ſuas ſimul conſe〈que〉ntes
eadem erunt proportione. Quare ſicut duæ BC cum AD ad duas
AD cum BC, ita duæ RP cum PS ad duas P S cum PR,
verùm duæ quidem RP cum PS eſt vtra〈que〉 ſimul SR RP. bis
enim aſſumitur PR, ſemel verò PS. Cum autem lineæ DH ES
à lineis diuidantur ęquidiſtantibus ED OT HM, erit DK
KH, vt ER ad CS; kD verò eſt æqualis KH, erit ER ipſi
RS ęqualis. erit igitur ER cum RP, hoc est PE ipſis SR RP
ęqualis. duæ verò PS cum PR eſt vtra〈que〉 PS SR. bis enim aſ­
ſumitur PS, ſemel què PR. & quoniam FS eſt ęqualis ipſi SR.
quod quidem eodem modo oſtendetur, cùm ſit FS ad SR, vt
BH ad Hk. erit FS cum SP, hoc est PF ipſis PS SR æqualis.
Quare ita ſehabet PE ad PF, vt duæ BC cum AD ad duas
AD cum BC. Centrum igitur grauitatis P trapezij ABCD
in linea eſt EF, quæ coniungit parallelas AD BC bifariam di
1uiſas; ita vt pars PE, quæ eſt ad minorem parallelam AD
reliquampartem PF eam habet proportionem, quam du
ipſius BC, quæ eſt maior æquidiſtantium, vna cum min
AD, ad duplam minoris AD cum maiore BC, ergo demons
ta ſunt, quæ propoſita fuerant.
ex 2.ſ
13.hu
8. huius.
ex proxi­
me demon
ſtratis.
*
13. huius.
6. hu
1. ſe.
15. p
29. p
ex 4.
11. 〈que〉
18.
corol
quint
cor.2
ma a
huius
1. l.
in 13
71[Figure 71]
SCHOLIVM.
Græcus codex poſt ea verba, cùm ſit HB tertia pars ipſius Z
habet και δια τοῡ θ σαμιου ω̄αζἀλλλος τἀ βὰσει ὀυχ τᾱς ἁ μθ, qu
quidem verba illa οὐκ τὰς perperam leguntur; quorum l
ponerem αομὶνα ἐσὶ, ita vt ſint hoc modo reſtituenda, κα δια
σαμε̄ιου ω̄αζάλλλως τᾱ βὰσει αομὲνα ισὶ ἁ μθ.
*
Hæc ſunt, quæ de centro grauitatis figurarum rectiline
Archimedes ſcripta reliquit. Ex quibus maxima certè vtil
habetur; ne〈que〉 ampliùs de rectilineis figuris Archimedes p
tractare voluit. ex dictis enim alia omnia dependent. Nan
tra grauitatis rectilinearum figurarum, quæ æquales angu
latera〈que〉 æqualia habent, ex his in uenire poterimus. quæ
dem figurę in circulo inſcribi poſſunt. Quod ſanè Federi
Comandinus in eius libro de centro grauitatis ſolidorum
prioribus propoſitionibus præſtitit. aliaquè nonnulla, vt
tragrauitatis rectilinearum figurarum in ellipſi, deindè ip
circuli, & ellipſis centra grauitatis in uenit. omneſquè dem
ſtrationes in ijs, quæ in hoc libro iam demonſtrata ſunt,
dauit. præterea ex his etiam idem Commandinus in com
tarijs libri Archimedis de quadratura paraboles, (quo ad p
xim) grauitatis centrum cuiuſlibet figurę rectilineæ ad in
nit. Quod quidem nos quo〈que〉, vt initio polliciti fuimus,
nullis mutatis idem oſtendemus. hoc prius ſuppoſito.
Triangula in eadem baſi conſtituta eam inter ſe propo
nem habent, quam eorum altitudines.
Hoc autem demonſtratum eſt ab excellentiſsimis viris,
riſquè Euclidis interpretibus, Federico Commandino, & Cl
ſtophoro Clauio; qui hanc propoſitionem poſt primam
ti libri Euclidis demonſtrarunt.
1
PROBLEMA.
Cuiuſlibet rectilineę figurę centrum grauitatis inuenire.
Triangulorum centrum grauitatis iam ab Archimede de­
monſtratum eſt.
Sit ita〈que〉 primùm quadri

laterum ABCD, cuius opor­
teat centrum grauitatis inue
nire. Ducatur AC, quæ qua
drilaterum in duo triangula
ABC ACD diuidet. à punctiſ­
què BD ad AC perpendicu
lares ducantur BE DF. In­
ueniantur deinde ex dictis cem
tra grauitatis triangulorum
ABC ACD. ſintquè puncta
GH. iungaturquè GH, quæ diuidatur in K, ita vt GK
ad KH ſit, vt DF ad BE. Dico punctum K centrum
eſſe grauitatis quadrilateri ABCD. Quoniam enim triangu­
la ABC ACD in eadem ſunt baſi AC, erunt inter ſeſe, vt al­
titudines. quare triangulum ACD ita ſe habet ad triangulum
ABC, vt DF ad BE. hoc eſt GK ad KH. punctum ergo K cem
trum eſt grauitatis magnitudinisex vtril què triangulis
ACD compoſitæ; hoc eſt quadrilateri ABCD.
ex 6.h
72[Figure 72]
Sit autem pentagonum

ABCDE. iunganturquè AC
AD. inueniaturquè triangu
li ABC centrum grauitatis
H. quadrilateri verò ACDE
ex proximè demom ſtratis cen­
trum grauitatis inueniatur
Iam vti〈que〉 conſtat (du­
cta HK) centrum grauita
tis totius ABCDE in linea
1HK exiſtere. Rurilus trianguli ADE centrum inueniatur F
quadrilateri verò ADCB punctum G. iungaturquè GF. e
eodem modo centrum grauitatis totius ABCDE in linea F
ſed eſt quo〈que〉 in linea HK, ergo vbrſe inuicem ſecant, vt
L, centrum erit grauitatis pentagoni ABCDE.
73[Figure 73]
In hexagonis ſimiliter.

vt ABCDEF iungantur
AC AE, deinceps inuenia
tur trianguli ABC centrum
grauitatis G, pentagoni
verò ACDEF ex dictis cen
trum ſit H. ductaquè GH
centrum grauitatis totius
ABCDEF erit in linea GH
ſimiliter centrum grauita­
tis trianguli AFE ſit K, pem
tagoni verò AEDCB ſit L, iunctaquè KL, erit centrum gr
uitatis totius hexagoni in linea KL. verùm eſt etiam in lin
GH. ergo errt in M. in quo GH KL ſe inuicem ſecant.
74[Figure 74]
Nequè aliter in heptago

no ABCDEFG, in quo du
cantur BG CE. trianguli
verò ABG centrum graui­
tatis ſit H. hexagoni autem
GBCDEF, ſit K. deinde
trianguli CDE centrum gra
uitatis ſit L, hexagoni ve­
rò CEFGAB ſit M. iun­
ctiſquè HK ML, eadem ra
tione centrum grauitatis
totius heptagoni erit in vtraquè linea Hk LM. ergo erit in
*
75[Figure 75]
Eodemquè prorſus modo in octagono, & in alijs demc
figuris centrum graui tatis inuenietur. quæ quidem facere
portebat.
1
Curautem hoc modo centra grauitatum in præfatis figu­
ris poſitione tantùm, & non determinatè ea indeterminata,
linea, & in tali ſitu exiſtere inuenerimus, vt in parallelogram
mis & in triangulis factum fuitab Archimede; explicabitur in
ſecundo libro poſt tertiam proportionem; vbi oſtendemus,
in quibus figuris determinatè inueniri poteſt centrum graui­
tatis.
Antequam autem finem primolibro imponamus, reliquum
eſt; vt ea quæ in præfatione ſuppoſuimus, oſtendamus. pri­
mùm què quando ſecundùm rectam lineam aliqua diuiditur
figura per centrum grauitatis, aliquando diuidi in partes ſem
per ęquales, & aliquando in partes inæquales.
PROPOSITIO.
Figura dari poteſt, quę per centrum grauitatis recta li­
nea diuiſa, ſemper in partes diuidatur æquales.
Sit parallelogrammum

ABCD, cuius centrum gra­
uitatis E. Ducaturquè per
E vtcun〈que〉; linea GEF, quę
vel diameter eſt, vel min^{9}.
ſi eſt diameter, iam conſtat
parallelogrammum in duo
ęqua eſſe diuiſum. Si verò non eſt diameter, ducantur
AC BD, quæ per E tranſibunt. Quoniam igitur AF eſt æqui­
diftans ipſi CG, eritangulus EAF ipſi ECG, & EFA ipſi
æqualis, eſt autem AEF ipſi GEC ad verticem æqualis, latus〈que〉
AE ipſi EC æquale; erit triangulum AEF triangulo CEG ęqua
le. eodemquè modo oſtendetur triangulum FEB triangulo
EGD. & triangulum AED ipſi BEC æquale. Ex quibus patet.
figuram ex tribus triangulis compoſitam, hoc eſt figuram
FGDA ipſi FGCB æqualem eſſe. diuiditurergo parallelogran­
mum à linea per centrum grauitatis ducta in partes ſem perç­
quales. quod demonſtrare oportebat.
1
34.primi
29. primi
15. primi
76[Figure 76]
Hoc idem multis alijs figuris accidet, vt pentagonis, he
gonisæquiangulis, & æquilateris, & alijs.
PROPOSITIO.
Figura dari poteſt, quæ per centrum grauitatis recta li
diuiſa, non ſemper in partes diuidatur ęquales.
Habeat triangulum ABC

latera AB AC æqualia. trian
guliverò centrum grauitatis ſit
D. à quo ipſi BC ęquidiſtans
Ducatur FDG. Dico partem
AFG minorem eſſe parte BFGC.
ducatur ADE, quæ bifariam
BC diuidet. & à puncto G
ipſi AE ęquidiſtans ducatur
HGK. compleantur〈que〉 figurę
EH KF. Quoniam enim FG
ęquidiſtans eſt ipſi BC, erit FD ad DG, vt BE ad E
& eſt BE ipſi EC æqualis. erit igitur FD ipſi DG ęqua
vt etiam paulò ante 15. huius oſtendimus. quare FG ip
DG dupla. eſt. ac propterea parallelogrammum FK dupi
eſt parallelogrammi DK. quia verò AD ipſius DE du
exiſtit, erit quoquè parallelogrammum DH ipſius DK
plum. Quare DH ipſi FK eſt æquale. At verò quoni
FG dupla eſt ipſius DG. erit triangulum AFG parallelog
mo DH æquale. triangulum igitur AFG parallelog
FK eſt æquale. Quare pars AFG parte BFGC minor
ſtit. quod demonſtrare oportebat.
ex 13. hui'
lemma an­
te ſecundam
demonſtra­
tionem 13 bu
ius.
ex 41.pri.
mi.
77[Figure 77]
Hinc perſpicuum eſt, eandem figuram per centrum gra
tatis diuiſam, aliquando in partes in æquales, aliquando in
tes æquales diuidi poſſe. in partes inęquales iam oſtenſum
hocaccidere perlineam FG. in partes verò æquales patet pe
neam ADE, quæ triangulum ABC in duo ęqua diuidi. t
gulum enim ABE triangulo: AEC eſt ęquale, cùm ſint
eadem altitudine, baſeſquè BE EC inter ſe ſint æquales.
1
1. ſexti.
Adhuc (veluti initio quo〈que〉 diximus) ſi fuerit prisma, vt
AB, cuius altera baſis ſit AC. tale verò ſit prisma, vt pl mum
AC planis CH CK &c. ſit erectum. ſit autem ipſius baſis
AC centrum grauitatis E. Dico ſi prima ſuſpendatur ex pu­

cto E, baſim AC horizonti æquidiſtantem permanere. vt co
gnoſcamusea, quæ his libris pertractantur, ad praxim poſſe
reduci. & ne aliquid abſ〈que〉 demonſtratione confirmatum re
linquamus. hoc quo〈que〉 oſtendemus. hoc pacto.
78[Figure 78]
Primùm quidem exijs, quæ demonſtrata ſunt, rectilineæ
figuræ AC centrum granitatis inueniatur E. eodemquè mo
do figuræ BD centrum grauitatis ſit F. Iungaturquè EF,
quæ bifariam diuidatur in G. Iam patet punctum G cen­
trum eſſe grauitatis priſmatis AB, ex octaua propoſitione Fe­
derici Commandini de centro grauitatis ſolidorum, & ex corol
lario quintæ propoſitionis eiuſdem libri, lineam EF late­
ribus AD CB ęquidiſtantem eſſe. quoniam autem plana CH
CK ad rectos ſuntangulos plano AC, erit CB eorum
nisſectio eidem plano AC perpendicularis. acpropterea EF
ipſi CB æquidiſtans plano AC perpendicularis exiſtit.
1Ita〈que〉 intelligatur ſolidum AB ex E ſuſpenſum; tunc ex
ma propoſitione de libra noſtrorum mechanicorum pon
AB ex E ſuſpenſum numquam manebit, niſi recta EG fu
horizonti perpendicularis. Quando autem EF erit horizc
ti perpendicularis, erit planum AC horizonti æquidiſtan
tunc. enim EF tum horizonti, tum plano AC perpendicul
exiſtet. Inuento igitur centro grauitatis E ipſius baſis A
ſi AB ſuſpendatur ex E, linea EGF in centrum mundi to
det; planumquè AC horizonti erit æquidiſtans. quod de
ſtrare oportebat.
19. v
mi.
14.vndeci
mi.
PRIMI LIBRI FINIS.
1
GVIDIVBALDI
E MARCHIONIBVS
MONTIS.
In Secundum Archimedis æ〈que〉ponderan­
tium Librum.
PRÆFATIO.
Secundus Archimedisliber, vtinitio primi
libri præfati ſumus, ſubtiliſſima theo­
remata ſpeculatur. Vultenim Archimedes
inueſtigare centrum grauitatis plani coni­
cæſectionis, quæ parabole paſſim vocatur.
quamuis Archimedes alio nomine, ac po­
tiùs deſcriptione quadam ſectionem hanc nun­
cuparit: veluti portio recta linea rectanguli〈que〉; coniſectione com tem
ta. Refert enim Eutocius Aſcalonita in principio ſui commen­
tarij in libros conicorum Apollonij Pergęi, ex ſententia Ge­
mini (cui Pappus etiam ex Ariſtęi ſententia aſſentire videtur)
quòd qui ante Apollonium fuerunt, perfectam, & abſolutam
conorum cognitionem

non habuerunt; inter
quos reſpoſuit Archime
de. Nam inquit conum deſi
nientes, ipſum per rectam
guli trianguli circumuo­
lutionem manente vno
eorum, quæ circa rectum
angulum ſunt, latere conſi­
derarunt. vt habetur in
definitionibus Euclidis
vndecimi libri elem en­
torum. vt Conus ABC fit
ex circumuoluto triangulo rectangulo ADC. conus verò EBC
ex triangulo EDC, & conus FBC ex rectangulo triangulo
1FDC. & ſi AD fuerit i­

pſi DC æqualis, conus
ABC vocabit rectan­
gulus. nam vtcumquè
ducto plano per axem,
quod triangulum faciat
ABC; erit angulus BAC
ad coniverticem rectus:
ſiquidem DAC recti di
midius exiſtit, veluti
DAB. pari ratione ſi ED
fuerit ipſa DC minor;
erit conus EBC obtuſi
angulus:nam ducto per axem plano, habebit triangulum
EBC angulum ad verticem coni BEC obtuſum; cùm ſit
BEC maior BAC. exiſtenteautem FD ipſa DC maiori, co
nus FBC acutiangulus nuncupabitur; quoniam triangulum
per axem FBC angulum ad verticem coni F acutum poſſide
bit; ſiquidem minor eſt BFC, quam BAC. Refert deinde,
quòd vnum〈que〉mquè
horum conorum eo­
dem modo piſci ſecue­

runt; vt ſit rectangu­
lus conus ABC; trian
gulum verò per axem
ſit ABC. in latere au­
tem AC quoduis ſu­
matur punctum D;
ducaturquè DE ad
AC perpendicularis;
& per DE ducatur pla
num plano ABC ere
ctum, quod quidem conum ſecet, ſectio autem ſit FDG. quę
ſanè eſt ſe ctio, quæ abipſis vocatur rectanguli coni ſectio,
quippè quæ ſi intelligatur terminata recta linea FG, nuncupa
tur portio recta linea, rectanguli〈que〉 coni ſectione contenta.
1
3. primi co
mcorum A
pol.
21. primi.
79[Figure 79] 80[Figure 80] 81[Figure 81]
Si verò conus

ABC fuerit obtu
ſiangulus, ſitquè
triangulum per
axem ABC, eo­
dem modoà quo­
uis puncto D, du
cta DE ad re­
ctos angulos ipſi
AC, acper DE
ducto plano ad
planum ABC erecto, quod conum ſecet, vt FDG; erit FDG
obtuſianguli coni ſectio, quæ vnà cum recta FG vocatur por­
tio recta linea, obtuſianguliquè coni ſectione contenta.
82[Figure 82]
Similiter exiſtente co­

no acutiangulo ABC,
cuius triangulum per a­
xem ſit ABC. & à puncto
D ducta ſit DE perpen­
dicularis ipſi AC, du­
ctoquè plano per DE ad
planum ABC erecto, e­
rit DFEG acutianguli
coni ſectio.
83[Figure 83]
Apollonius au-­
tem Pergęus, qui ab­
ſolutiſſima commenta­
ria de conicis ſcripſit,
huiuſmodi conos omnesvocauit rectos; ad differentiam coni
ſcaleni. coni enim rectiaxes habent baſibus erectos. ſcaleni ve
rò nequaquam. & in ſcalenis latera triangulorum per axem
non ſunt ſemper æqualia. quod ſemper conis rectis contingit.
Preterea ſectionem rectanguli coni parabolen nominauit;
obtuſianguli verò coni ſectionem hyperbolen; ſectionem au
tem acutianguli coni ellipſim nuncupauit. & in vnoquo〈que〉
cono tàm recto, quàm ſcaleno has tres ineſſe ſectiones demom
1ſtrauit. Ex quibus colligit Geminus (〈que〉m Eutocius, alijquè
complures ſecuti ſunt) eos, qui ante Apollonium extitere,
conostantùm rectos cognouiſſe. & in vnoquo〈que〉 cono vnam
tantùm ſectionem animaduertiſſe. quod quidem ſi de ijs, qui
ante Archimedem fuere intelligatur; ad mitti fortaſſe poterit;
ac præſertim de Euclide. vt patet ex definitione coni abeo
tradita. At verò de Archimede, qui poſt Euclidem, ante verò
Apollonium fuit, non ita facilè concedendum videtur. Nam ex
ijs, quæ ſcripta reliquit. eum non ſolùm notitiam ha-­
buiſſe de conis rectis; verùm etiam de ſcalenis facilè ex i-­
pſius ſcriptis conijci poteſt. In primo enim librode ſphæ­
ra, & cylindro multis in locis, vt in ſeptima, octaua, no
na, decimaquarta, decimaquinta propoſitione; alijsquè in
locis conos nominat ęquicrures, quod quidem ſecundum i­
pſum ſunt, qui in eius ſuperficie æquales habent rectas lineas
à vertice coni ad baſim ductas. item in epiſtola quo〈que〉 libri
de conoidibus & ſphęroidibus, quam Archimedes Deſitheo
ſcribit. cùm de obtuſiangulo conoideverba facit, conum vo­
catæquicrurem. Quòd ſi Archimedes hos conos vocauit æ­
quicrures, cui dubium, ipſum eosad differentiam eorum, qui
non ſunt æquicrures ita nuncupaſſe? qui verò non ſunt æ­
quicrures ex ipſomet Apollonio ſunt ſcaleni; nam æquicrures
hoc modo coni axes habent baſibus erectos. qui igitur non
erunt æquicrures, eorum axes ſuis baſibus nunquàm erunt e­
recti. Præterea idem quo〈que〉 confirmari poteſt ex demon­
ſtratione vigeſimæquintæ propoſitionis eiudem libri, in qua
cùm nominet Archimehes conum rectum proculdubiò ad
differentiam eorum, qui non ſuntrecti ita eum nuncupauit.
nam ſi Aichimedes (ex illorum ſententia) conos tan ùm re­
ctos cognouiſſet; quorſum his in locis conum rectum, vel æ­
quicrurem nominaſſet? ſat ſibi fuiſſet conum tantum dixiſſe.
Ne〈que〉 verò dicendum eſt Archimedem per cono recto intel
lexiſſe conum rectangulum eo modo, 〈que〉m ſupra expoſui­
mus. nam in ea propoſitione, dum conſtituit hunc conum,
non conſurgit conus rectangulus, ſed obtuſiangulus quapro
pter conum rectum nominatad differentiam coni ſcaleni. Cę
terùm ut manifeſtè oſtendamus Archimedem conos
1uiſſe ſcalenos, conſideranda eſt octaua propoſitio libri de co­
noidibus, & ſph æroidibus, in qua proponit Archimedes co­
num conſtituere, & inuenire, in quo ſitſectio ellipſis data, ver
tex autem coni in linea exiſtat a centro ellipſis adectos angu
los ellipſis plano erecta. Exqua conſtructione planè apparet,
Archimedem (vt ex eius demonſtratione conſtat) hoc in lo­
co 〈que〉rere, & inuenire conum proculdubio ſcalenum. vt etiam
ex nona eiuſdem libri propoſitione perſpicuum eſſe poteſt; in
qua vt plurimùm conus inuenitur ſcalenus. Ex quibus mani­
feſtiſſimè patet Archimedem non ſolùm de conis rectis, verum
etiam de conis ſcalenis notitiam habuiſſe. Porrò ea verba, quę
refert Eutocius ex ſententia Heraclij, qui Archimedis vitam
literis mandauit; idipſum ſatis manifeſtant. Heraclius enim
inquit Archimedem quidem primum conica theoremata fuiſſe
aggreſſum; Apollonium verò, cùm ea inueniſſetab Archime
de nondum edita; tanquam eius propria edidiſſe. quod qui­
dem etiam exipſiusmet Archimedis ſcriptis confirmari poteſt.
in libro nam〈que〉 de conoidibus, & ſphæroidibus ante quartam
propoſitionem vbi Archimedes theorema proponit alibi de­
monſtratum, inquit, Hoc autem oſten ſum eſt in conicis elementis. in
principio etiam libri de quadratura paraboles, cùm nonnulla
propoſuiſſet; poſt tertiam propoſitionem ſcilicet, inquit De­
monſtrata autem ſunt hæc in elementis conicis. nonneigitur conſtat
Archimedem elementa conica ſcripſiſſe? Obijciet verò aliquis,
non propterea conſtare, hęc elementa eonica, quorum me­
minit Archimedes, ipſiusmet eſſe Archimedis; cùm non affir
met, hæcfuiſſe ab ipſo demonſtrata. verùm illud in primis ma
nifeſtum eſt, tempore Archimedis conica elementa extitiſſe.
vt nonnulli Euclidem quatuor conicorum libros edidiſſe af­
firmant; ſicut Pappus in ſeptimo Mathematicarum collectionuum
libro aſſerit. Sed ex modo lo〈que〉ndi Archimedis planè conſtat
hæc fuiſſe ab ipſo conſcripta. Nam quando Archimedes ali­
qua ſupponitab alijs demonſtrata, tunc addere conſueuit, illa
ab alijs demonſtrata eſſe; vt in vndecima propoſitionedeco­
noidibus, & ſphæroidibus; cùm inquit. omnis coni ad conum pro­
portionem compoſitam eſſe ex proportione baſium, & proportione altitu­
dinum, quod quidem, quia ab alijs demonſtratum fuerat,
1tim inquit, demonſtratum eſt ab iis, qui ante nos fuerunt. ſimiliter
in libro de ſphęra, & cylindro ante propoſitionem decimam
ſeptimam, cùm nonnulla ſuppoſuerit ab alijs demon ſtrata in
quit. Hæc autem omnia à ſuperioribus ſunt demonſtrata. In ſecunda
verò parte quintę propoſitionis hui^{9} ſecudi libri cu inquit, De
monſtratum eſt enim aliis in locis portiones ſeſquitertias eſſe triangulorum.
quod quia ipſemet aſſecutus eſt in libro de quadratura para­
boles, idcircò non addit ab ipſomethoc oſtenſum fuiſſe. A­
liaquè huiuſmodi loca breuitatis ſtudio omitto oſtendentia
ea, quæ Archimedes ſupponit tanquam demonſtrata, quando
non additab alijs oſtenſa eſſe, à ſe ipſo demonſtrata fuiſſe, vt
in demonſtratione decimæ quartę propoſitionis primi libri,
nec non ex octaua huius ſecundi libri demonſtratione; alijſ­
què locis perſpicuum eſſe poteſt. Quare tùm ex præfntis Archi
medis locis, tùm Heraclij teſtim onio manifeſtè elicipoteſt,
Archimedem elementa conica ſcrip ſiſſe. Ne〈que〉 verò quicqua
nos turbare debet, quòd Apollo nius coni ſectionibus nomina
impoſuerit; ſi tamen ipſe prim us fuit; cùm eas proprijs nomi­
nibus, vt potè parabolen, hyperbolen, & ellipſim nuncupet;
& in quolibet cono omnes agnouerit ſectiones. Nam quam­
uis vſ〈que〉 ad Archimedis tempus hi termini nondum extite­
rint; & in ſingulis conis priſci illi vnicam tantùm cognouerint
ſectionem; Archimedes tamen vlteriùs progreſſus eſt. etenim
hæc quo〈que〉 ſectionum nomina ipſi fortaſse minùs ignota fue­
runt: quandoquidem in demonſtratione nonæ propoſitio­
nis de conoidibus, & ſphęroidibus ellipſim nominat. Pręte­
rea non ſolùm cognouit Archimedes conos ſecari poſſe pla­
nis lateribus coni erectis, verùm etiam alijs modis: quod qui­
dem exemplo ellipſis manifeſtari optimè poteſt. Nam in o­
ctaua propoſitione eiuſdem libri ellipſes latus coni ad angu­
los rectos minimè ſecant. veluti quo〈que〉 in nona propoſitione
idem ſępè contingit. At verò in eodem adhuc libro ante primam pro
poſitionem inquit Archimedes. Si conus plano ſecetur cum omnibus
eius lateribus coeunti, ſectio vel erit circulus, vel acutianguli coni ſe­
ctio. Vnde perſpicuum eſt non in vno duntaxat cono acutian
gulo, verùm in omnibus conisſectionem ellipſis cognouiſſe.
Præterea ex hoclo〈que〉ndi modo li〈que〉t ipſum ſectionem quo
1〈que〉 nouiſſe ſubcontrariam; quæ cùm ſit baſi ſubcontraiſè po
ſita, oina latera coni ſecat; & tnm non eſt ellipſis, ſed qua­
propter ſi in omnibus conis ellipſis nouit ſectionem; cur in i­
pſis, & parabolas, & hyperbolas minùs animaduertit? cùm
ſit manifeſtum ex dictis in cono obtuſiangulo & hyperbolem
& ellipſim; in rectangulo autem parabolem, ellipſimquè co­
gnouiſſe? hòc certè non eſt aſſerendum. Ex hoc enim perſpi­
cuum eſt Archimedem cognouiſſe conos ſecari poſſe planis,
quæ non ſint ſemper ad coni latus erecta. dormitaſſequè Eu­
tocium Geminum, & alios ſecus hac in parte de Archimede
ſentientes. Ampliùs non ne cognouit etiam Archimedes ſeca­
ri poſſe rectangulos conoides, itidemquè & obtuſiangulos pla
nis, quæ ne〈que〉 ſint per axem ducta, ne〈que〉 axi æquidiſtantia;
ne〈que〉 ſuper axem erecta. vt in duodecima, decimatertia, &
decima quarta propoſitione eiuſdem libri patet. quomodo i­
ta〈que〉 his quo〈que〉 modis 〈que〉mlibet conum ſecari poſſe igno­
rauit? Non eſt igitur ambigendum Archimedem cognouiſ­
ſe conos ſecari poſſe planis ad latus coni differentem inclina­
tionem habentibus. Ex quibus perſpicuum eſt, ipſum in om­
nibus conis omnes ineſſe ſectiones omnino animaduertiſſe.
At ſi concedamus etiam ſua tempeſtate nondum ſectioni­
bus ipſis propria fuiſſe impoſita nomina; tam eam parabo­
lem, quæ erat rectanguli coni ſectio; quàm quæ erat ſectio
alterius coni, cùm ſit eadem ſectio, eodem nomine nuncu­
pabat; nempè rectanguli coni ſectionem. Et hoc, quia
priùs hæc ſectio cognita ſuit in cono rectangulo (vnde ſi­
bi nomen vindicauit) quam in alio. quod idem dicen­
dum eſt de alijs ſectionibus. Vt manifeſtum eſſe poteſt
exemplo ſectionis acutianguli coni. Archimedes enim eo­
dem loco, anteprimam ſcilicet propoſitionem de conoidi
bus, & ſphęroidibus inquit, Si cylindrus duobus planis æquidi­
stantibus ſecetur; quæ cum omnibus ipſius lateribus coeant, ſectio­
nes, uelerunt circuli; uel conorum acutiangulorum ſectiones. vo­
catigitur Archimedes acutianguli coni ſectionem, tam coni
ſectionem, quàm ſectionem cylindri. veluti etiam in decimatertia,
& decimaquarta propoſitione eiuſdem libri acutianguli coni ſe­
ctio ab ipſo ea nuncupatur ſectio, quæ oina latera tam conoidis
1rectanguli, quàm obtuſianguli abſcindit. dum modo non ſit
ad axem erecta. nullaquè alia de cauſa hæ ſectiones omnes i­
dem acutianguli coni ſectionis nomen obtiuerunt; niſi quia
priùs hæc ſectio à cono acutiangulo nomen accepit, quando­
quidem in ipſo fortaſse primùm cognita fuit, quaàm in alijs.
Ex dictis ita〈que〉 manifeſtum eſt, ſententiam Heraclij veram
eſſe poſſe, & rationi valdè conſentaneam; Archimedem ſcili
cet elementa conica ſcripſiſſe; Apollonium què, cùm ea ab Ar
chimede nondum edita inueniſſet, ſicut propria ſua edidiſſe.
Omitto interim multa ab Archimede in eius libris ſupponi,
quæ non niſi in conicis eſſe dcbebant, quæ quidem habentur
ſolùm in conicis Apolloni. Negandum tamen non eſt, vt
Eutocius quo〈que〉 affirmat, ipſum Apollonium multa auxiſſe,
multaquè ad conica ſpectantia adinueniſſe. vt ipſemet Apol­
lonius in epiſtola ad Eudemum fatetur. cùm tamen non ſit
ſemperfacilè inuentis addere. Sed de his hactenus. ſat ſit au­
tem nouiſſe, Archimedem, quando in hoclibro nominat por
tionem recta linea, rectanguliquè coni ſectione contentam,
eam ſignificare fectionem, quæ parabole nuncupatur.
1
5. primi co
nicorum A­
poll.
GVIDIVBALDI
E MARCHIONIBVS
MONTIS.
IN SECVNDVM ARCHIMEDIS
ÆQVEPONDERANTIVM
LIBRVM.
PARAPHRASIS
SCHOLIIS ILLVSTRATA.
84[Figure 84]
PROPOSITIO. I.
Si duo ſpacia recta linea, & re
ctanguli coni ſectione conten
ta, quæ ad datam rectam lineam
applicare poſſumus, non ha
beantidem grauitatis centrum;
magnitudinis ex vtriſ〈que〉 i­
pſorum compoſitæ centrum
grauitatis erit in recta linea, quæ ipſorum centra
grauitatis coniungit; ita diuidens dictam rectam li
neam, vt ipſius portiones permutatim eandem ad
inuicem proportionem habeant, vt ſpacia.
1 85[Figure 85]
Sint duo ſpacia AB CD, qualia dicta ſunt. ipſorum autem centra
grauitatis ſint puncta EF. iungaturquè EF, quæ diuidatur in
H; & quam proportionem habet AB ad CD, eandem habeat FH
ad HE. oſtendendum eſt magnitudmis ex utriſquè AB CD ſpa­
ciis compoſitæ centrum grauitaias eſſe punctum H. ſit quidemipſi EH
utra〈que〉 ipſarum FG FK æqualis; ipſi autem FH, hocest GE
(ſuntenim EH GF æquales, à quibus dempta communi
GH remanent EG HF ęquales) ſit æqualis EL. & quoniam
FH eſt æqualis LE, & FK ipſi EH, erit & LH ipſi KH
æqualis. Cùm autem ſit FH ad HE, vt AB ad CD; ipſi
verò FH vtra〈que〉 ſit æqualis LE EG. ipſi autem HE vtra­
〈que〉 æqualis GF FK, erit etiam ut LG ad Gk, ita AB ad CD.
cùm ſit LG ad GK, vt FH ad HE; aupla enim est utra〈que〉
EG GK utriuſ〈que〉 FH HE. At uerò circa punctum E ipſius
AB, quod eſt eius centrum grauitatis, ex utra〈que〉 parte lineæ LG,
ipſi LG æquidistantes ducantur MO QN, quæ æqualiter ab
LG diſtent, ductis ſcilicet MQ ON æquidiſtantibus, ſint
LM LQ GO GN inter ſe æquales; ita ut ſpacium MN ſit
ſpacio AB æquale: quod quidem applicatum eſt ad lineam LG.
erit uti〈que〉 ipſius MN centrum grauitatis punctum E. cùm ſit pun­
ctum E in medio lineæ LG, quæ bifariam diuidit latera
oppoſita MQ ON parallelogrammi MN. compleatur ita­
〈que〉 ſpacium NX. habebit quidem MN. ad NX proportionem,
1quam habet QN ad NP, hoceſt LG ad GK. habet autem &
AB ad CD proportionem ipſius LG ad GK. ut igitur AB ad
CD, ſic est MN ad NX. & permutando vt AB ad MN, ita
CD ad NX. æquale autem est AB ipſi MN, erit igitur & CD
ipſi NX æquale. Centrum autem grauitatisipſius NX est punotum
F. propterea quod eſt in medio lineæ GK, parallelo­
grammi NX oppoſita latera ON XP bifariam ſecat. &
quoniam æqualis eſt LH ipſi HK, totaquè LK appaſita latera MQ
XP bifariam diuidit, totius PM centrum grauitatis erit punctum Hr
Verùm ipſum MP æquale est utriſ〈que〉 MN NX, quorum, cùm
ſint centra grauitatis EF, æ〈que〉pondera bunt ſpacia MN
NX ex diſtantijs FH HE. ſi igitur loco parallelo gram mo­
rum MN NX ponatur AB in E, & CD in F, cùm ſit
AB ipſi MN, & CD ipſi NX æquale; ſpacia AB CD
diſtantijs FH HE æ〈que〉ponderabunt. ac propterea magnitudi
nis ex utriſ〈que〉 AB CD compoſitæ centrum grauitatis eſtpunctum
H. quod quidem propoſitum fuit.
2. cor. 9.
primihui^{9}.
16.quinti.
2.cor. 9.
primihui^{9}.
8.poſthui^{9}
SCHOLIVM.
Cùm ſit intentio Archimedis non nulla pertractare ad pa­
rabolen ſpectantia; primùm iacit fundamentum, parabolas
nempe ita ſe habere, vt permutatim diſtantiæ, ex quibus
ſuntcollocatæ, ſe habent. & quamuis vniuerſim, atquè in om­
nibus mutuam hanc conuenientiam ex dictis ex primo libro
depræhendere liceat, hoc tamen loco peculiariter voluitad
huberiorem do ctrinam id ipſum in parabolis
& quamuis in primo libro dixerit Archimedes magnitudi­
nes æ〈que〉ponderare, quando ita ſe habent inter ſe, ut diſtan­
tiæ permutatim ſe habent; hocautem loco quærit centrum gra
uitatis magnitudinis ex parabolis compoſitæ; non ſunt tamen
propoſitiones diuerſæ. nam & in primo libro dum in demon
ſtratio ne quærit proportionem diſtantiarum, oſtendit, vbi
nam ſit centrum grauitatis magnitudinum. quare quannis pro
poſitiones videantur diuerſæ, non ſunt tamen diuerſæ, ete­
nim vt poſt tertiam primi libri propoſitionem adnotauimus,
1hæc planèſe conſequuntur, vt exempli gratia in figura pun­
ctum H centrum eſt grauitatis magnitudinis ex vtriſ〈que〉
AB CD compoſitæ. ergo AB, & CD ex diſtantijs HEHF
æ〈que〉ponderant. & è contra. hoc eſt AB CD æ〈que〉ponde­
rant ex diſtantijs EH HF. ergo punctum H centrum eſt
grauitatis magnitudinis ex vtriſ〈que〉 AB CD compoſrtæ; cum
ſit EHF recta linea. Solent autem mathematici aliquando
eandem propoſitionem pluribusmedijs demonſtrare; idcirco
conſiderandum eſt, Archimedem in hac propoſitione alio v­
ti medio ad oſtendendum punctum H centrum eſie graui­
tatis, quo uſus eſt in ſexta propoſitione primi libri. cùm in pri
mo libro per diuiſionem magnitudinum, diuiſio nem què di
ſtantiarum vniuerſaliter domonſtret centrum grauitatis ma­
gnitudinum. hoc autem loco per parallelogramma MN
NX parabolis æqualia, & circa centra grauitatis EF conſti­
tuta, in uenit centrum grauitatis magnitudinis ex vtriſ〈que〉 pa
rallelogrammis MN NX compoſitæ. quod eſt quidem pun­
ctum H. medium nempè totius parallelogrammi MP.
quod idem punctum H centrum eſt grauitatis vtriuſ〈que〉 pa
raboles AB CD in EF collocatæ.
6.7.primi
huius.
ex 9.& 10
primihui^{9}.
Ex his obſeruandum occurrit, hanc eſſe peculiarem metho
dum, qua poſſumus quorumlibet planorum æ〈que〉pondera­
tionem oſtendere; hoc eſt plana ex diſtantijs eandem permu
tatim proportionem habentibus, vt eadem met plana, æ〈que〉­
ponderare; dum modo ipſis æqualia parallelogramma conſti
tuere poſſimus. ac propterea ſupponit Archimedes, nos poſſe
applicare ad rectam lineam ſpacium æquale ſpacio recta li­
nea, rcctanguliquè coni ſectione contento. quod quidem ſpa­
cium ſupponit parallelogram mum exiſtere, cùm pun­
ctum E centrum ſit grauitatis ſpacij MN, eſt F
ſpacij NX. punctum verò H totius PM. quòd ſi MN
NX & MP non eſſent parallelogramma, ne〈que〉 puncta EFH
eorum centra grauitatis exiſterent. vt ex demonſtranone pa­
tet. ſuppoſuit tamen Archimedes nos poſſe applicare ad re­
ctam lineam parallelogrammum æquale ſpacio recta linea,
rectanguliquè coniſectione contento; quia duplici medio in
1libro de quadratura paraboles, propoſitione ſcilicet decimaſe
ptima, & vigeſimaquarta, docuit quamlibet portionem recta
linea, rectanguliquè coni ſectione contentam ſeſquitertiam
eſſe trianguli eandem ipſi baſim habentis, & altitudinem ęqua
lem. Ex qua propoſitione facilè conſtat nos parabolę ſpacium
ad rectam lineam applicare poſſe, vt propoſitum fuit hoc
modo.
PROBLEMA.
Ad datam rectam lineam datę parabolę ęquale parallelo­
grammum applicare, ita vt data linea oppoſita parallelogran­
mi latera biſariam diuidat.
86[Figure 86]
Data ſit parabole
ABC, ſitquè data recta
linea GK. oportet ad
GK parallelogrammum
applicare æquale por­
tioni ABC, ita vt GK
bifariam diuidat oppo
ſita parallelogram mi
latera. Conſtituatur ſu
per AC triangulum ABC,
qd baſim habeat AC,
eandem〈que〉 portionis
altitudinem; quod quidem
fiet, inuenta diametro DB, quæ parabolen in B ſecet, iunctiſ〈que〉
AB BC. eritvti〈que〉 parabole ABC trianguli ABC ſeſquitertia.
Ita〈que〉 diuidatur AC in tria ęqualia, quarum vna pars ſit
producaturquè AC. fiatquè CL ipſi CH ęqualis erit ſanè AL
ipſius AC ſeſq uitertia. Et obid (iuncta BL) erit triangulum
ABL trianguli ABC ſeſquitertium. ſunt quippè triangula
ABC inter ſe, vt baſes AL AC. ac per conſe〈que〉ns triangulum
ABL patabolę ABC exiſtit ęquale. Applicetur ita〈que〉 ad
GK parallelogrammum GS ęquale triangulo ABL. erit GS
1
læ ABC ęquale. deinceps ducatur NP ipſi GK
ęquidiſtans, quę bifariam diuidat oppoſita latera GR
KS. producanturquè RG SK. fiantquè GO KX ę­
quales ipſis GN KP. iungaturquè OX; erit nimi-­
rum parallelogram mum OP ipſi GS ęquale. qua­
re parallelogram mum OP parabolę ABC exiſtit ę­
quale. Applicatum eſt igitur ad GK parallelogram­
mum expoſitę parabolę ęquale. lineaquè GK paralle­
logrammi OP bifariam diuidit oppoſita latera ON
XP. quod fieri oportebat.
44. ſecundi
conicorum
Apoll.
17. 24. Ar
ch. dquad.
patab.
1.ſexti.
ex 44.pri­
mi.
87[Figure 87]
Si in portione recta linea rectanguliquè coni
ſectione contenta triangulum inſcribatur, eandem
baſim cum portione habens, & altitudinem æqua
lem: & rurſus in reliquis portionibus triangula in­
ſcribantur, quæ eaſdem baſes cum portionibus
habeant, & altitudinem æqualem; ſemper què in
reſiduis portionibus triangula eodem modo
inſcribantur: figura, quæ in portione oritur,
planè inſcribi dicatur. Patet quidem lineas
1huius figuræ inſcriptæ angulos, qui ſunt vertici
portionis proximi, eoſquè deinceps coniungen­
tes, baſi portionis æquidiſtantes eſſe; bifariamquè
à diametro portionis diuidi; diametrum verò in
proportione diuidere numeris deinceps impari­
bus. vno deno minato ad verticem portionis. Hoc
autem ordinate oſtenſum eſt.
SCHOLIVM.
Scopus Archimedis in hoc ſecundo libio, vt initio primi
diximus, eſt inuenire centrum grauitatis paraboles. & vt de­
ducatnos in hanc cognitionem, quadam vtitur figura rectili­
nea in parabole inſcripta, quę plurimùm conducit, & eſt tam
quam medium ad inueniendum hoc grauitatis centrum. his
igitur verbis docet, quo modo in parabole in ſcribenda ſit hęc
figura; in quibus multa quo 〈que〉 proponit tanquam ſit pro­
poſitio quædam; in qua multa ſint oſtendenda. quorum ta­
męn demonſtrationem omiſit, ac tanquam ab eo alibi de­
monſtratam. Horum autem ex Apollonij Pergęi conicis
demonſtrationem elicere quidem potuiſſemus. at quoniam
Archimedes ipſe non nulla ad hæ cſpectantia alijs in locis de­
monſtrauit ideo Archimedem per Archimedem declarare o­
portunum magis nobis viſum eſt.
Sit portio contenta recta linea, rectanguliquè coni ſectio­
ne ABC, cuius diameter BD. Iunganturquè AB BC, diuida­
tur deinde AB bifariam in E, a quo ipſi BD æquidiſtans
1ducatur EF, eritvti 〈que〉 punctum F vertex portionis AFB.
vt Archimedes demonſtrauit in libro de quadratura parabo­
les propoſitione decimaoctaua. iungantur〈que〉 AF FB. rur
fus bifariam diuidantur AF FB in punctis GH, à quibus
ipſi BD ducantur æquidiſtantes GI HK b eandem cau­
ſam erit punctum I vertex portionis AIF. K verò portio­
nis FKB. connectanturquè AI IF FK KB. eademquè pror
fus ratione ad alteram partem inſcribantur triangula CLB

CML, & LNB. Primùm quidem triangulum ABC dicitur
planè inſcriptum, vt Archimedes ipſe infra in demonſtratio­
nibus quintæ, ſextæ, & octauæ propoſitionis nominat. Dein
de figura AFBLC, figuraquè AIFKBNLMC dicuntur in
portione planè inſcriptæ. figuraquè AFBLC vna cum AC
pentagonum in portione planè inſcriptum dici pont. vt Archime
des in ſecunda parte demonſtrationis quintæ propoſitionis
huius libri nuncupat. ideòquè erit AIFKBNLMC nonago­
num in portione planè inſcriptum. & ita in alijs. Connectam
1tur KN FL IM, quæ diametrum BD ſecent in punctis
STV. oſtendendum eſt, lineas KN FL IM baſi AC ęqui
diſtantes eſſe. deinde diametrum BD lineas KN FL IM
bifariam in punctis STV diuidere poſtremo lineas KN F
IM ita diametrum BD diſpeſcere, vt poſito vno BS, linea ST
ſit tria, TV quin〈que〉; & VD ſeptem. Producantur FE KH
ad RX. quoniam enim FR eſt æquidtans BD, erit AE
EB, vt AR ad RD; eſt〈que〉 AE ipſi EB æqualis ergo AR i­
pſi RD æqualis exiſtit. eodem què modo oſtendetur FX æ­
qualem eſſe XT. quandoquidem eſt FX ad XT, vt FH ad
HB. ſimiliterquè ad alteram partem, exiſtentibus LO NP i­
pſi BD æquidiſtantibus, erit DO ipſi OC æqualis, & TP
ipſi PL. quod quidem eodem prorſus modo demonſtrabi­
tur. Quoniam autem AC bifariam à diametro diuiditur in
puncto D, erit DR ipſi DO æqualis, cùm vnaquæ〈que〉 ſit
dimidia ipſarum AD DC æqualium. eſt igitur RD dimidia
ipſius AD, quæ dimidia eſt baſis AC. quod idem euenit ipſi
DO. quare BD ſeſquitertia eſt ipſius FR, & ipſius LO, ex de­
cimanona Archimedis de quadratura paraboles. ac propterea
eandem habet proportionem BD ad FR, quam ad LO.
ſequitur FR æqualem eſſe ipſi LO. & obid FL ipſi AC æ­
quidiſtantem eſſe. & FT ipſi RD, & TL ipſi DO ęqualem.
vnde FT ipſi TL ęqualis exiſtit. eadem quèratione prorſus in
portione FBL oſtendetur KN ipſi FL, ac per conſe〈que〉ns i­
pſi AC ęquidiſtantem eſſe. & KS ipſi SN æqualem exiſte­
re. Producatur IG ad Z, quæ ipſam AB ſecet in 9. linea ve­
rò LO ſecet BC in 〈que〉 ductaquè MY ipſi BD æquidiſtans
ipſam ſecet BC in α. & quoniam IZ eſt æquidiſtans FR, e­
rit AG ad GF, ut A9 ad 9E, & AZ ad ZR. & eſt AG
GF æqualis, erit igitur A9 ipſi 9E, & AZ ipſi ZR æquaiis.
Eodemquè modo oſtendetur Cα ipſi αQ, & CY ipſi YO ę­
qualem eſſe. quo niam autem in portione AFB a dimidia baſi
ducta eſt LF, à puncto autem 9, hoc eſt à dimidia dimidię ba
ſis AB (eſt enim E9 dimidia ipſius AE, quæ dimidia eſt baſis
AB) ducta eſt 9I diametro æquidiſtans, erit EF ſeſquitertiai­
pſius I9 pari〈que〉 ratione oſtendetur QL ſeſquitereiam eſſe i­
pſius Mα quare vt FE ad I9, ita LQ ad Mα. obſimilitudinem
1 autem triangulorum ABD AER ita eſt BD ad ER, vt DA
ad AR. eadem〈que〉iatione ita ſehabet BD ad QO, vt DC
ad CO. Sed vt DA ad AR, ita eſt DC ad CO, eſt quip
pe DA ipſius AR dupla, veluti DC ipſius CO. quare i­
 ta erit BD ad ER, vt BD ad QO. ac propterea ER ipſi
QO ęqualis exiſtit. oſtenſa verò eſt RF ęqualis OL, reli­
quaigitur EF reliquæ QL eſt æqualis, quia verò ita eſt FE
ad I9, vt QL ad Mα, erit permutando FE ad QL, vt I9

ad Mα. ſuntquè FE QL ęquales, ergo I9 ipſi Mα ęqua­
lis exiſtit. quoniam autem ob trianguſoium ſimilitudinem
AER A9Z, ita eſt AR ad AZ, vt ER ad 9Z. ob ſimili­
tudinem vero triangulorum QOC αYC ita eſt CO ad CY,
vt QO ad αY: & eſt RA ad AZ, vt OC ad CY, cùm
vtrę〈que〉 in dupla exiſtant proportione; et ER ad 9Z, vt
QO ad αY. & permutando ER ad QO vt 9Z ad αY. eſt
vero ER ipſi QO, æqualis, ergo 9Z ipſi αY ęqualis exiſtit. at
vero oſtenſa eſt I9 ęqualis Mα; to ta igitur IZ ipſi MY eſt
1æqualis, quæ cùm ſintipſi BD æquidiſtantes, erunt & inter ſe­
ſe parallelæ. quare IM ipſi AC eſt æquidiſtans. ita­
〈que〉 AR eſt æqualis CO, & horum dimidia, hoc eſt RZ ipſi
OY æqualis erit. atqui DR eſt ipſi DO æqualis; ergo DZ ipſi
DY exiſtit æqualis. ipſi verò DZ eſt æqualis IV, & ipſi DY æ­
qualis VM. eruntigitur IV VM inter ſe equales. Iam
oſtenſum eſt, lineas KN FL IM, quę coniunguntangulos fi
guræ in parabole planè inſcriptæ, ipſi AC æquidiſtantes eſſe.
Diametrum què BD ipſas in punctis STV bifariam diſpeſcere.
2. lemma.
9. quinti.
ex 33.34
primi.
2.ſexti.
ex 4.ſexti.
11. quinti.
9. quinti.
16. quinti.
ex 11.quin
ti 16.quu
33.primi.
34.primi.
88[Figure 88] 89[Figure 89]
Quoniam ita〈que〉 in portione FBL à dimidia baſi ducta eſt
TB, a dimidia verò dimidiæ baſis ducta eſt XK, erit ſeſ­
quitertia ipſius KX, hoc eſt ipſius ST. eſt enim KT parallelo­
grammum, & ST ipſi KX æqualis. Si igitur ponatur BT
quattuor, erit ST tria, & BS vnum. ſimiliter quoniam
ſeſquitertia eſt ipſius FR, hoc eſt ipſius TD, cùm ſit TD ipſi
FR ęqualis. ſi ita 〈que〉 ponatur BD ſexdecim, erit vnaquæ〈que〉
FR TD duodecim. & TB quattuor, vt poſitum fuit. Quoniam
autem (vt diximus) eſt BD ad ER, vt DA ad AR, erit BD du­
pla ipſius RE. quare ſi BD eſt ſexdecim, erit RE octo. & quo­
niam eſt FR duodecim, erit EF quatuor. eſt autem FE ipſius
I9 ſeſquitertia, erit igitur I9 tria. & quoniam eſt ER ad 9Z, vt
RA ad AZ, erit ER dupla ipſius 9Z. ac propterea erit 9Z quat
tuor, cum ſit ER octo, & eſt 9I tria, tota ergo IZ, hoc eſt DV,
ſeptem exiſtet. ſed quoniam eſt DT duodecim, cuius pars
DV eſt ſeptem, eritreliqua VT quin〈que〉. Poſito igitur BS v­
no, erit ST tria, TV quin〈que〉, & VD ſeptem. quod erat quo­
〈que〉 demonſtrandum. Et hæc ſunt quę ab Archimede pro­
poſita fucrant.
19.Archi­
medis de
quad. pa­
rab.
34. primi.
Ex his tamen nonnulla quo〈que〉 colligemus ad ea, quæ ſe­
quuntur neceſſaria. ac primùm quidem conſtat BD quadru­
plam eſſe ipſius BT, & ipſius FE.
1
Oſtenſum eſt enim BD ſexdecim eſſe, & BT quatuor, & FE
itidem quatuor exiſtere. Ex demonſtratione autem Archime
dis decimæ nonæ ptopoſitionis de quadratura paraboles cla­
rè elicitur BD quadruplam eſſe ipſius BT.
Ex quibus etiam ſequitur FE QL inter ſe æquales eſſe. am­
bo enim ſunt, vt quatuor.
90[Figure 90]
Præterea oſtendendum eſt triangulum AFB triangulo BLC
ęquale eſſe, portionem què paraboles AFB portiom BLC ęqua
lem. Ampliùs triangulum AIF triangulo CML, & portio­
nem AIF portioni CML æqualem eſſe, & reliqua triangula
reliquis triangulis, acportiones portionibus ęquales eſſe.
Ex vigeſima prima propoſitione Archimedis de quadratu­
ra paraboles triangulum ABC vniuſcuiuſ〈que〉 trianguli AFB
BLC eſt octuplum. ergo ad ambo eandem hent proportionem. qua
re triangula AFB BLC inter ſe ſunt ęqualia. At vero quoniam
1portio AFB trianguli AFB eſt ſeſquitertia,
portio BLC trianguli BLC, eritportio AFB ad triangulum
AFB, vt portio CLB ad triangulum CLB, & permutando
portio AFB ad portionem CLB, vt triangulum AFB
ipſum CLB triangula verò ſunt æqualia; ergo portiones AFB
CLB inter ſe ſunt æquales. Eademquè ratione triangulum AFB
octuplum eſt trianguli AIF, & triangulum CLB octuplum
ipſius CML. vnde triangula AIF CML ſunt æqualia. et ea­
rum quo〈que〉 portiones AIF CML ſunt æquales, ſiquidem
ſunt triangulorum ſeſquitertiæ. Et hoc modo reliqua trian­
gula FKB LNB, & portiones FKB LNB oſtendentur æqua­
les. cùm ſit triangulum FBL dictorum triangulorum octu­
plum. quod oportebat quo〈que〉 demonſtrate.
9. quinti.
17.24. Ar
chimedis
de quad.
parab.
16. quimi
21.Archi­
medis de
quad. pa­
rab.
His demonſtratis ſequitur Archimedes quaſi connectens ſe
〈que〉ntem propoſitionem cumijs, quæ ſuppoſita ſunt, inqui­
ens, ſi autem & in portione &c.
PROPOSITIO. II.
Si autem & in portione rectalinea, rectangu­
li〈que〉 coni ſectione contenta, figura rectilinea pla
ne inſcribatur, inſcriptæ figuræ centrum grauita­
tis erit in diametro portionis.
1
Sit portio ABC, qualis dicta eſt, & in ipſa planè inſcribatur recti­
linea figura AEFGBHIKC. portionis verò diameter ſit BD. oſten-
dendum eſt, rectilineæ figuræ centrum grauitatiseſſe in linea BD. ium
gantur GH FI EK. quę ipſi AC, & inter ſe ęquidiſtantes
erunt. hę verò lineæ diametrum BD ſecent in punctis NML

Quoniam enim lineæ GH FI EK bifariam ſunt à diame­
tro BD diuiſæ in punctis NML, trapezium AEKC duas
habebit line as æquidiſtantes AC EK, quas bifariam diuidit
DL, quare trapezii AEKC centrum grauitatis est in LD. at ob
eandem cauſam trapezii EFIK centrum est in ML; trapezii verò
FGHI centrum est in MN. lineæ enim LM MN bifariam
diuidunt parallela latera EK FI GH, ſed & trianguli etiam
GBH centrum grauitatis eſt in BN. quippè cùm BN ipſam
GH bifariam diuidat. perſpicuum eſt totius rectilineæ figuræ
AEFGBHIKC centrum grauitatis eſſe in linea BD. quod de­
monſtrare oportebat.
1
exdemom
stratis.
15. primi
huius.
13. primi
huius.
91[Figure 91]
SCHOLIVM.
Ecce qúo Archimedes incipit inueſtigare centrum graui
tatis paraboles. nam ex hoc, quod oſtendit centrum grauita­
tis figuræ in portione planè inſcriptæ eſſe in diametro por­
tionis, ſtatim colliget in quarta propoſitione centrum graui­
tatis paraboles in diametro quo〈que〉 ipſius portionis exiſtere.
interponit autem Archimedes ſe〈que〉ntem propoſitionem. nam
antequam inueniat centrum grauitatis paraboles, opus habet
prius oſtendere centra grauitatis duarum, & vt ita dicam om
nium parabolrum diametros in eadem proportione ſecare.
ad quod demonſtrandum, hanc paſſionem figuris planè inſcri­
ptis priùs accidere oſtendit. potuiſſetquè Archimedes priùs quar
tam propoſitionem oſtendere, quam tertiam; ſe〈que〉ntem ve­
rò propoſitionem immediatè poſuit poſt ſecundam, ordo e­
nim ſic poſtulat. etenim ambæ deijs pertractant, quæ rectili­
neis figuris plane inſcriptis accidunt. Pręterea earum demon
ſtrationes ferè circa eadem verſantur, cùm ijsdem rectis lineis
in portionibus eodem modo ductis vtantur; ob ſe〈que〉ntis ve­
rò propoſitionis intelligentiam hęc priùs oſtendemus.
92[Figure 92]
LEMMA I.
Eandem habeat proportionem AB ad CD, quam habet
GH ad KL. CD verò ad EF eam, quam habet kL ad MN. ſintquè
1AB CD EF inter ſe ęquidſtantes. ſimiliter GH KL MN
æquidiſtantes, ſintantem ductæ BDF HLN rectæ lineæ; ſit­
què BD ad DF, vt HL ad LN. ſitquè maior AB quàm
CD, & CD, quàm EF. vnde erit quoquè GH maior KL,
& KL, quam MN. iunctiſquè AC CE, & GK KM.
Dico ſpacium ACDB ad ſpacium CEFD eandem habere
proportionem, quam ſpacium GKLH ad ſpacium KMNL.
93[Figure 93]
Producantur AC CE, quæ cum BF conueniant in OP.
productæquè GK KM cum HN conueniant in QR.
concurrentenim, quoniam CD KL ſunt minores ipſis AB
GH, & EF MN minores ipſis CD KL. Fiatquè vt AB
ad CD, ita CD ad V. & vt GH ad kL, ita KL ad X.
deinceps CD ad EF, ita EF ad Y. & vt KL ad MN,
ita MN ad Z. Quoniam igitur triangulum ABO ſimile
eſt triangulo CDO, cùm ſit CD æquidiſtansipſi AB. ha
bebit triangulum ABO ad CDO, proportionem, quam ha
bet AB ad CD duplicatam. hoc eſt quam hab et AB ad
V. Eodemquè modo oſtendetur triangulum GHQ ad KLQ
ita eſſe, vt GH ad X quia verò AB CD V ita ſe habent,
vt GH kL X, erit ex æquali AB ad V, & GH ad X.
triangulum igitur ABO eandem habet proportionem ad
1CDO, quam triangulum GHQ ad KL〈que〉 quare diuiden­
do ſpacium ACDB ad triangulum CDO eſt, vt
GKLH ad triangulum kL〈que〉 Rurſus quoniam ob triangu
lorum ſimilitudinem ABO CDO, ita eſt AB ad CD,
BO ad OD. ſimiliter ob ſimilitudinem triangulorum GHQ
KLQ ita eſt GH ad kL, vt HQ ad QL. & eſt AB ad CD,
vt GH ad KL, erit BO ad OD, vt HQ ad QL. & diui­
dendo BD ad DO, vt HL ad L〈que〉 deinde conuertendo DO
ad DB, vt LQ ad LH. & eſt BD ad DF, vt HL ad LN,
ex ęquali DO ad DF, vt LQ ad LN. Quoniam autem ſimi
lium triangulorum CDP EFP latus CD ad latus EF ita ſe
habet, vt DP ad PF. ſimiliter exiſtentibus ſimilibus triangu
lis KLR MNR ita eſt KL ad MN, vt LR ad RN, & vt CD
ad EF, ita eſt KL ad MN, erit DP ad PF, vt LR ad
& per conuerſionem rationis PD ad DF, vt RL ad LN. &
conuertendo DF ad DP, vt LN ad LR. diximus autem OD
ad DF ita eſſe, vt QL ad LN, & eſt DF ad DP, vt LN ad
LR. ergo ex ęquali erit OD ad DP, vt QL ad LR. At
quoniam ita eſt OD ad DP, vt triangulum OCD ad PCD,
& vt QL ad LR, ita eſt triangulum QKL ad triangulum RKL,
erit OCD ad PCD, vt QKL ad RKL. Quoniam autem triam
gula CDP EFP ſunt ſimilia, triangulum CDP ad
EFP proportionem habebit, quam CD ad EF duplicatam,
hoc eſt quam habet CD ad Y, cùm ſint CD EF Y propor­
tionales. ſimiliter ob triangulorum KLR MNR ſimilitudi­
nem triangulum KLR ad MNR, ita erit vt KL ad Z, eſt au­
tem CD ad Y, vt KL ad Z, erit igitur triangulum CDP ad
EFP, vt KLR ad MNR, & diuidendo ſpacium CEFD ad
gulum EFP, vt ſpacium KMNL ad triangulum MNR. & com
uertendo triangulum EFP ad ſpacium CEFD, vt triangulum
MNR ad ſpacium KMNL. Ita〈que〉 quoniam oſtenſum eſt i­
ta eſſe ſpacium ACDB ad triangulum CDO, vt ſpacium
GKLH ad triangulum KL〈que〉 & vt triangulum CDO ad trian
gulum CDP, ita triangulum KLQ ad triangulum KLR, dein
de, vt triangulum CDP ad triangulum EFP, ita triangulum
KLR ad triangulum MNR; deniquè vt triangulum EFP ad
ſpacium CEFD, ita triangulum MNR ad ſpacium kMNL,
1 erit ex æquali à primo ad vltimum ſpacium ACDB ad ſpacium
CEFD, vt ſpacium GKLH ad ſpacium KMNL. quod demom
ſtrare oportebat.
11. ſexti.
9. ſexti.
22 quinti.
17. quinti.
eſt 4.ſexti
17.quinti.
cor.4. quim
ti.
22. quinti
ex 11. quim
ti.
cor. 19.
quinti.
22. quinti
ex 1.ſexti.
19. ſexti.
ex quinti.
cor.4. quim
ti.
22. quinti
LEMMA II.
Æquidiſtantes verò lineę AB CD ita ſe habeant, vt æquidi­
ſtantes EF GH, ſitquè maior AB, quàm CD, & EF, quam
GH. & ſuper CD GH ſint triangula CDP GHR, ſint〈que〉; BDP
FHR rectæ lineæ, & vt BD ad DP, ita ſit FH ad HR. iunctis〈que〉;
AC EG. Dico ſpacium ACDB ad triangulum CDP ita eſſe, vt
ſpacium EG HF ad triangulum GHR.
94[Figure 94]
Eadem enim prorſus ratione productis AC EG, quæ cum
BP FR conueniant in OQ, oſtendetur ſpacium AD ad trian
gulum CDO ita eſſe, vt ſpacium EH ad triangulum GH〈que〉 &
eſſe OD ad DB, ut QH ad HF. & quoniam eſt BD ad DP, vt
FH ad HR, erit ex ęquali OD ad DP, vt QH ad HR. & vt OD
ad DP, ita eſt triangulum CDO ad triangulum CDP, & vt
QH ad HR, ita triangulum GHQ ad GHR. cùm ita〈que〉 ſit
AD ad CDO, vt EH ad GHQ, & vt CDO ad CDP, ita
GHQ ad GHR. ex æquali erit ſpacium AD ad triangulum
CDP, vt ſpacium EH ad triangulum GHR. quod demonſtra
re oportebat.
1
22 quinti.
. ſexti.
22. quinti.
LEMMA. III.
95[Figure 95]
Sit A ad CD, vt E ad FG, diuidan
tur〈que〉; CD FG in eadem proportione in HK,
ita vt ſit CH ad HD, vt FK ad KG.
Dico A ad DH ita eſſe, vt E ad KG.
A verò ad CH, vt E ad Fk.
Quoniam enim ita eſt CH ad HD, vt FK ad kG; e­
rit componendo CD ad DH, vt FG ad GK. eſt autem
ad CD, vt E ad FG; CD verò eſt ad DH, vt FG ad GK; er
go ex æquali A erit ad DH, vt E ad GK. quo­
niam eſt GH ad HD, vt FK ad kG; erit
DH ad HC, vt GK ad KF. rurſus igitur ex æquali A e­
rit ad CH, vt E ad FK. quod oſtendere oportebat.
18.qumti.
22 quinti.
cor.4.quin­
ti.
PROPOSITIO. III.
Si in vtra〈que〉 duarum ſimilium portionum recta linea re
ctanguliquè coni ſectione contentarum rectili­
neæ figuræ planè inſcribantur; figuræ verò inſcri­
ptæ latera inter ſe multitudine æqualia habeant;
rectilinearum centra grauitatum portionum dia­
metros ſimiliter ſecabunt.
1 96[Figure 96]
Sint duæ portiones ABC XOP, in ipſiſquè planè in ſcribantur recti­
lineæ figuræ AEFGBHIKC XSYQOZVTP; quæ omnia latera
inter ſe numero æqualia habeanta, Diametri verò portionum ſint BD
1OR. iungantur〈que〉; Ek FI GH. quæ inter ſe, & ipſi AC çquidiſtantes
erunt; bifariam què à diametro BD in punctis LMN diuiſæ e­
runt. Iungantur ſimiliter & ST YV QZ, quas bifariam dia­
meter OR in punctis 9αβ diuidet. eruntquè ductæ lineæ ipſi
XP, & inter ſe æquidiſtantes. Quoniam igitur BD diuiditur à lineis
æquidiſtantibus GH FI EK in proportionibus numeris deinceps impa­
ribus; poſito enim vno BN, eſt quidem NM tria, ML quin〈que〉,
& LD ſeptem. ſed & RO ſimiliter à lineis QZ YV ST in pro­
portionibus diuiditur numeris deinceps imparibus, eadem. enim
ratione ſi ponatur Oβ vnum, erit βα tria, α9 quin〈que〉;, & 9R
ſeptem. & portiones ipſorum diametrorum BD OR ſunt numero æ
quales. quot.n ſunt BN NM ML LD, tot ſunt Oβ βα α 9 9R. pa
tet diametrorum portiones in eadem eſſe proportione, vt 〈que〉m admodum
eſt BN ad NM, & NM ad ML, & ML ad LD, ita eſſe Oβ ad
βα, & βα ad α9, & α9 ad 9R. Atverò quoniam ita eſt DB ad BL,
vt RO ad O9; (ſunt.n.ut ſexdecim ad nouem) & ut DB ad
ita eſt quadratum ex AD ad quadratum ex EL; & vt RO ad O9,
ita eſt quadratum ex XR ad quadratum ex S9; erit quadratum ex
AD ad quadratum ex EL, vt quadratum ex XR ad ex S9 quadratum.
ergo ut AD ad EL, ita XR ad S9. & horum dupla nempè AC ad
EK, vt XP ad ST: eadem〈que〉; prorſus ronne, quoniam ita eſt
ad BM, vt 9O ad Oα (ſunt.n.ut nouem ad quatuor) oſtendetur
EL ad FM ita eſſeut S9 ad Yα, & horum dupla, ſcilicet EK ad FI
ita eſſe, ut ST ad YV. Cùm〈que〉; ſit MB ad BN, vt αO ad Oβ, ut ſci
licet quatuor ad vnum; ſimiliter oſtendetur FM ad GN ita eſſe
vt Yα ad Qβ; FI uerò ad GH, vt YV ad QZ. vnde colligitur non
ſolùm portiones diametrorum (ut dixim us) in eadem eſſe pro­
portione, ſed & parallelas AC EK FI GH, & XP ST YV QZ in
eadem eſſe proportione. & T rapeziorum ipſius quidem AEkC, & ipſius
XSTP centra grauitatum eſſe in lineis LD 9R ſimiliter poſita, cùm
eandem habeant proportionem AC EK, quam XP ST. lineæquè
LD 9R bifariam diuidant ſuas æquidiſtantes AC EK.
& XP ST. etenim ſi ponatur trapezij AK centrum graui
tatis γ, ipſius vcrò XT centrum grauitatis δ, erit Lγ ad γD,
vt dupla ipſius AC cum EK ad duplam ipſius
cum AC. & 9δ ad δR erit, vt dupla ipſius XP cum
ST ad duplam ST cum XP. quoniam autem ita eſt AC ad EK,
1
[Empty page]
1vt XP ad ST, & antecedentium dupla, hoc eſt dupla i­
pſius AC ad EK erit, vt dupla ipſius XP ad ST.
& componendo dupla ipſius AC cum EK, vt i­
pſius XP cum ST ad ST. At verò EK ad duplam
ipſius EK, ita eſt, vt ST ad duplam ipſius ST, ſed
ad AC eſt, vt ST ad XP, erit EK ad vtraſ〈que〉 conſe­
〈que〉ntes ſim ul ſumptas, hoc eſt ad duplam ipſius EK cum
AC, vt ST ad ſuas conſe〈que〉ntes, nempe ad duplam ipſius
ST cum XP. Ita〈que〉 quoniam ita eſt dupla ipſius AC
cum EK ad Ek, vt dupla ipſius XP cum ST ad ST, & eſt EK
ad duplam ipſius EK cum AC, vt ST ad duplam ipſius
ST cum XP. erit ex ęquali dupla ipſius AC cum EK ad
plam ipſius EK cum AC, vt dupla ipſius XP cum ST ad
duplam ipſius ST cum XP. ac propterea ita eſt Lγ ad γD,
vt 9δ ad δR, & ob id centra γδ erunt in lineis LD 9R ſi­
militer poſita. Rurſus eodem modo (ne eadem ſæpiùs repetan
tur) Trapeziorum EFIk SΓVT centragrauitatum, quæ ſint εζ, ſi
militer hoc eſt in eadem proportione diuident lineas LM 9α, i­
ta vt ſit Lε ad εM, vt 9ζ ad ζα. & in trapezits FH ΓZ centra
grauitatum Ηκ ſimiliter diuident MN αβ, ita ut MΗ ad ΗN ſit, vt
ακ ad κβ ſed & triangulorum GBH QOZ centra grauitatum λμ
in lineis B N Oβ erunt ſimiliter poſita, ſiquidem Bλ ad λN eſt,
Oμ ad μβ; quippè cùm in dupla ſint proportione. eandem au­
tem habent proportionem Trapezia, & triangula: Nam cùm
ſit AD ad EL, vt XR ad S9, & ut EL ad FM, ita S9 ad Y;
eſtquè DL ad LM, ut R9 ad 9α, cùm ſint, vt ſeptem ad quin
〈que〉; erit ſpacium AL ad ſpacium EM, vt ſpacium X9 ſpa­
cium S. ſimiliterquè oſtendetur DK ad LI ita eſſe, vt RT
ad 9V. quare totum trapezium AK ad EI eſt, vt XT ad SV.
pariquè ratione oſtendeturita eſſe trapezium EI ad FH, vt
SV ad YZ. quia verò ita eſt FM ad GN, vt Yα ad Qδ,
eſt autem MN ad NB, vt αβ ad βO, ſunt quippè ut tria ad
vnum, erit ſpacium FN ad triangulum GBN, vt
Yβ ad triangulum QβO. codemquè modo oſtendetur ita
eſſe ſpacium IN ad triangulum BNH, vt ſpacium Vβ ad
triangulum OβZ. Ex quibus ſequitur ita eſſe trapezium FH
ad triangulum BGH, vt trapezium YZ ad triangulum OQZ.
1
[Empty page]
1ſi ita〈que〉 diuidatur γε in ν, ita ut ſit εν ad νγ, vt trapezium AK
ad EI. erit punctum ν centrum grauitatis figurę
ſimiliquè modo diuidatur δζ in <10>, ita vt ſit ζ<10> ad <10>δ, vt trape
zium XT ad SV; erit punctum <10> grauitatis centrum figuræ
XSYVTP. quia verò ita eſt AK ad EI, vt XT ad SV, erit εν
ad νγ, vt ζ<10> ad <10>δ. Diuidatur aunt deinceps λΗ in σ, ſit〈que〉; λσ ad σΗ, vt
FH ad triangulum BGH, erit punctum σ centrum grauitatis
figuræ FGBHI. eademquè ratione diuidatur μκ in τ, ſitquè
μτ ad τκ, vt YZ ad triangulum OQZ; erit punctum τ cen­
trum grauitatis figuræ YQOZV. ſed eſt FH ad BGD, vt YZ
ad OQZ, erit igitur λσ ad ση, vt μτ ad τκ. Quoniam autem
ita eſt Ak ad EI, vt XT ad SV, erit componendo
ad EI, vt figura XSYVTP ad SV; & eſt EI ad FH, vt SV
YZ. ergo ex æquali figura AEFIKC erit ad FH, vt figura
XSYVTP ad YZ. eſt autem FH ad BGH, vt YZ ad OQZ. e­
ritigitur figura AEFIKC ad ſuas conſe〈que〉ntes, ad
ſcilicet FGBHI, vt figura XSYVTP ad ſuas conſe〈que〉ntes, hoc
eſt ad figuram YQOZV. Diuidatur ita〈que〉 σν in χ, ita ut σχ
ad χ ſit, vt figura AEFIKC ad figuram FGBHI, erit
χ centrum grauitatis totius figurę AEFGBHIKC. ſimiliter di­
uidatur τ<10> in ξ, ſit〈que〉 τξ ad ξ<10>, ut figura XSYVTP ad figu­
ram YQOZV, erit punctum ξ centrum grauitatis totius fi­
guræ XSYQOZVTP. quia verò ita eſt figura AEFIKC ad fi
guram FGBHI, vt figura XSYVTP ad figuram YQOZV. e­
rit σχ ad χν, vt τξ ad ξ<10>. Ita〈que〉 quoniam BD ad DL eſt, vt σν
ad R9, cùm ſin^{4} utſexdecim ad ſeptem. & eſt Lγ ad γD, vt 9δ
ad δR, erit BD ad Lγ, vt σν ad 9δ. & vt BD ad γD, ita OR
δR. rurſus quoniam BD ad LM eſt, vt OR ad 9α, nempe vt ſex
decim ad quin〈que〉; & eſt Lε ad εM, ut 9ζ ad ζα, erit BD ad εL,
vt OR ad 9ζ. eſt verò BD ad Lγ, vt OR ad 9δ; erit igitur BD ad
vtram 〈que〉 ſimul εL Lγ, hoc eſt ad εγ, vt OR ad ζδ. ſed quoniam
eſt γν ad νε, vt δ<10> ad <10>ζ, erit BD ad γν, vt OR ad δ<10>. eſt autem BD
ad Dγ, vt OR ad Rδ, vt dictum eſt, ergo BD ad Dν eſt, vt OR
ad R<10>. ſimiliterquè oſtendetur BD ad BA ita eſſe, vt OR ad Oτ.
Cùm ita〈que〉 ſit BD ad DR, & ad Bσ, ut OR ad R<10>, & ad Oτ; e­
rit BD ad DR Bσ ſimul, vt OR ad R<10> Oτ ſimul, & permutan­
do tota BD ad totam OR, vt ablata DνBσ ad ablatam R<10>οτ.
1 ergo & reliqua σν ad reliquam τ<10> eſt, ut tota BD ad totam OR.
rurſuſquè permutando σν ad BD ut τ<10> ad OR, conuertendo〈que〉;
BD ad σν eſt, ut OR ad τ<10>, Quia verò ita eſt σχ ad χν, ut τξ ad ξ<10>;
erit BD ad σχ, vt OR ad τξ atverò BD ad bσ eſt, vt OR ad Oτ.
erit igitur BD ad Bχ, ut Oγ ad Oξ. ac propterea diuidendo Dχ
ita ſe habet ad χB, vt Rξ ad ξO. Quare manifestum est totius recti­
lineæ figuræ in portione ABC inſcriptæ centrum grauitatis χ in eadem
proportione diuidere BD, veluti centrum grauitatis ξ figuræ rectilineæ
in portione XOP inſcriptæ ipſam OR diametrum. quod demonstra­
re oportebat.
ex iis quę
poſt pri­
mi huius
demonſtra
ta ſunt.
3. Archi.
de quad.
parab. &
20, primi
conicorum
Apoll.
22. ſexti.
15. primi
huius.
15. primi
buius.
18. quinti.
2. lemma an
te 13. pri
mi huius.
22. quinti.
ante 13.pri
mi huius.
1.lemma.
2.lemma.
ex 6. pri­
mi huius.
18. quinti.
22.quinti.
cor. 2. lem
ma m 13.
primi hui^{9}
ex 6. pri
mi huius.
3. lemma.
2. lemma an
te 13. pri
mi huius.
3. lcmma.
2. lemma an
te 13. pri­
mi huius
16.quinti.
19.quinti.
co.4.quinti.
3.lemma.
2. lemma
ante 13.
primi hui^{9}
18. quinti.
97[Figure 97] 98[Figure 98]
SCHOLIVM.
Hinc colligere licet parabolas omnes inter ſe ſimiles eſſe. Re
fert enim Eutocius hoc in loco, Apollonium pergęum in ſex
to Conicorum libro. (qui nondum in lucem prodijt) ſimiles
coni ſectiones dixiſſe eas eſſe, quando in vnaqua〈que〉 ſectione
lineę ducuntur baſi æquidiſtantes numero pares; hoc eſt tot in v­
na, quot in alia; vt in ſuperioribus figuris ductæ fuerunt, in v­
na quidem EK FI GH ipſi AC æquidiſtantes; & in altera ST
YV QZ ipſi PX æquidiſtantes; quę quidem efficiant, vt dia­
metri in eadem proportione diuiſæ proueniant; vt ſunt BN
NM ML LD; & Oβ βα α9 9R. Deinde æquidiſtantes AC EK
FI GH in eadem ſint proportione ipſarum XP ST YV QZ.
& quoniam hæ conditiones in omnibus poſſunt accidere pa
rabolis; vt ex ijs, quæ demonſtrata ſunt, manifeſtum eſt; id­
circo parabolæ omnes ſunt ſimiles. Ne〈que〉 verò exiſtimandum
eſt, quoniam parabolæ ſunt ſimiles, figur as quo〈que〉 planè
inſcriptas, vt AEFGBHIKC & XSYQOZVTP ſimiles eſſe in
ter ſe, ea præſertim ſimilitudine, qua ſunt figuræ rectilineæ;
vt ſcilicet anguli ſint æquales, & circum ęquales angulos late­
ra proportionalia. in parabolis non attenditur hęc ſimilitudo.
ſatenim eſt, vt præfatæ adſint conditiones; ex quibus ſequi­
tur (vt oſtendimus) trapezia AK EI FH, triangulum què
BGH in eadem eſſe proportione trapeziorum XT SV YZ, ac
1trianguli OQZ. ac propterea quando Archimedes in propo
ſitione inquit ſi in vtra〈que〉 ſimilium portionum rectalmea, rectangu­
liquè coni ſectione contentarum, non propterda exiſtimandum eſt
reperiri poſſe aliquas parabolas recta linea terminatas no eſſe
ſimiles inter ſe; ea nimirumiam explicata ſimilitudine. ſunte­
nim Archimedis verba hoc modo intelligenda, nempè, ſi in
vtra〈que〉 portionum recta linea rectanguliquè coni ſectione
contentarum, quæ omnes ſunt ſimiles, & c. veluti ſi dicere­
mus. In ſimilibus ſemicirculis anguli omnes ſuntrecti. non
eſt intelligendum nonnullos ſemicirculos inter ſe diſſimiles
exiſtere poſſe. ſed hoc modo; in ſemicirculis, qui omnes ſunt
ſimiles, anguliſunt recti. Et hoc modo ſemperintelligere o­
portet, quando in ſe〈que〉ntibus Archimedes parabolas ſimiles
nominat. Nam & Archimedes cognouit omnes parabolas
inter ſe ſimiles eſſe; vt ipſe in demonſtratione octauæ propoſi
tionis huius ſupponere videtur. Oportebatenim aliquam in
parabolis demonſtrare ſimilitudinem, vt demonſtrari poſſet
centrum grauitatis in omnibus parabolis eſſe in certo, ac de­
terminato ſitu ipſius figuræ. in figuris enim, quæ aliquam in­
terſe non habent ſimilitudinem, in ipſis centrum grauitatis
determinari minimè poſſe videtur. Dicet autem fortaſſe ali­
quis, determinatur tamen centrum grauitatis in omnibus triam
gulis, quæ quidem interſe non ſuntſimilia. Cui reſponden­
dum; triangula omnia inter ſe ſimilia non eſſe ſimilitudine
rectilinearum figurarum, nempè vt anguli ſintæquales, & cir­
cum æqualesangulos latera proportionalia. quòd tamen nul­
lam inter ſeſe habeant conuenientiam, omnino negatur. nam
triangula omnia ſimul quodam modo illam habent conue­
nientiam, & ſimilitudinem; quæ parabolis accidit.
In triangulis enim ABC DEF ductę ſint AG DH ab angu­
lis ad dimidias baſes. ſintquè diuiſa triangulorum latera in ea
dem proportione, in punctis kL, OP. & vt AK KL LB, ita ſit
AM MN NC, & DQ QR RF. ductiſquè KM LN OQ
quæ lineas AG DH ſecent in punctis ST VX; primùm quidem
erunt KM LN OQ PR baſibus BC EF æquidiſtantes; quas
lineæ AG DH in punctis ST VX bifariam diuident, cùm ſit
1BG ad GC, vt LT ad TN, & KS ad SM. & ut EH ad HF ita
PX ad XR, & OV ad V〈que〉 Deinde erunt AG DH à lineis KM
LN OQ PR in eadem proportione diuiſæ; ſiquidem ita eſt
AS ST TG, ut DV VX XH. cùm ſint, ut expoſitæ propor­
tiones AK KL LB, & DO OP PE. Præterea erit ſpacium,
BN ad LM, vt ER ad PQ, & LM ad triangulum AK M,

vt PQ ad triangulum DO〈que〉 Nam quoniam triangulu AEC
ſimile eſt triangulo ALN, oblatus LN ipſi BC æquidiſtans;
erit ABC ad ALN, ut AB ad AL duplicata. eodemquè modo
erit DEF ad DPR, vt DE ad DP duplicata; eandem autm,
habet proportionem AB ad AL, quam DE ad DP: quadoqui
dem latera AB DE in eadem ſunt proportione diuiſa; erit igi­
tur triangulum ABC ad ALN, vt triangulum DEF ad DPR.
ſimiliterquè oſtendetur ALN ad AkM ita eſſe, ut DPR ad
DO〈que〉 Quoniam autem ABC eſt ad ALN, ut DEF ad DPR,
diuidendo erit BN ad ALN, ut ER ad DPR. Atverò quoniam
ALN ad AKM eſt, vt DPR ad DO〈que〉 erit per conuerſio­
nem rationis ALN ad LM, vt DPR ad P〈que〉 qua­
 re ex ęquali BN eſt ad LM, ut ER ad P〈que〉 Cùm auem ſit
ALN ad AKM, ut DPR ad DO〈que〉 erit diuidendo LM ad
AKM, vt PQ ad DO〈que〉 Quocirca erit ſpacium BN ad
LM, vt ER ad PQ, & LM ad triangulum AKM,
vt PQ ad triangulum DO〈que〉 Ex quibus perſpicuum
eſt omnia triangula aliquam inter ſe habere ſimilitudinem,
ex qua poſſibile fuit determinare in omnibus ſitum, vb
1ritur centrum graurtatis. Quòd ſi figurę nullam conuenien­
tiam, nullamquè ſimilitudinem inter ſe habuerint; ut in qua
drilateris, pentagonis, & reliquis figuris, quæ inter ſe ne〈que〉
latera ne〈que〉 angulos ęquales habeant; & propterea nullam in­
terſe conuenientiam, & ſimilitudinem habere poſſunt; im­
poſſibile quidem eſſet in ipſis determinare ſitum centri grauita
tis; ita vt omnibus quadrilateris, ac omnibus pentagonis quo
modo cun〈que〉 factis, & ita cęteris figuris deſeruire poſſit. Cum
exempli gratia in pentagonis modò in vno, modò in alio ſi­
tu centrum reperiatur; prout ſunt diuerſę figuræ. Poſſumus
quidem in vnaqua〈que〉 figura reperire punctum poſitione,
quod ſit quidem centrum grauitatis illius determinatæ figu­
ręt. vt in fine primilibri oſtendimus. eſſet tamen impoſſibile
in omnibus proprium certum, ac determinatum ſitum repe­
rire; vt ſcilicet ſit in tali linea, taliquè modo diuiſa, vtomnib^{9}
pentagonis, & hexagonis, cæteriſquè huiuſmodi deſeruire
poſſit. vt determinatur in triangulis, & vt determinari poteſt
in quadrilateris; quæ vel ſint parallelogramma, vel duo ſaltem
latera ſint æquidiſtantia. cùm in his conuenientia, quàm
triangulis accidere oſtendimus, reperiatur; quandoquidem
ſunt triangulorum portiones. ſimiliter in parallelogrammis fa
cilè erit oſtendere aliquam inter ſe ſimilitudinem exiſtere. pen­
tagona verò hexagona, & cæteræ figuræ, quæ angulos æqua­
les, & æqualia latera habent; iam conſtat ſimilia eſſe inter ſe.
præterea circuliomnes ſunt ſimiles. Ellipſes quo〈que〉 inter ſe
aliquam habent ſimilitudinem, in quibus deſcribitur figura,
planè inſcripta. vt perſpicuum eſt in libro Federici Comman
dini de centro grauitatis ſolidorum. ac propterea in his, & in
alijs, quibus inter ſe aliqua ſimililudo reperiri poteſt, centrum
quo〈que〉 grauitatis determinari poterit.
ex 2.ſexti
ex lèmate
im ſecundam d
monſtratio­
ne. pri­
mi huius.
17. quinti.
coro. 19.
quinti.
22. quinti.
99[Figure 99]
LEMMA.
Sint quatuor magnitudines ABCD. ſitquè A maior B;
&C maior D. Dico A ad D maiorem habere proportio­
nem, quàm habet B ad C.
1
Hoc à nobis oſtenſum fuitinitio tractatus devecte in no­
ſtris mechanicishoc pacto.
100[Figure 100]
Quoniam enim A ad C maiorem habet pro
portionem, quam B ad C; & A ad D maiorem
quo〈que〉 habet proportionem, quàm habetad C;
A igitur ad D maiorem habebit, quàm B ad C.
quod demonſtrare oportebat.
8. quinti.
PROPOSITIO. IIII.
Omnis portionis recta linea, rectanguliquè co
ni ſectione contentæ, centrum grauitatis eſt in dia
metro portionis.
101[Figure 101]
Sit portio, vt dicta eſt, ABC; cuius diameter ſit BD. demon­
ſtrandum est dictæ portionis centrum grauitatis eſſe in linea BD. ſi.n.
non, ſit punctum E. & ab ipſo ducatur ipſi BD aquidistans EF; at­
〈que〉 in portione inſcribatur triangulum ABC eandem baſim AC
habens, & altitudinem portioni æqualem. & quam proportionem
habet CF ad FD, eandem habeat triangulum ABC ad ſpacium
1k. in portione autem planè inſcribatur figura rectilinea AGBNC, ita
vt relictæ portiones AOG GPB BQN NRC ſimul ſint minores
ipſo K. inſcriptæ quidem rectilineæ figuræ centrum grauitatis est in linea
B D. ſit punctum H. connectaturquè HE, & producatur; & à pun
cto C ipſi B D ducatur æquidistans CL. Quoniam autem por
tiones AOG GPB BQN NRC ſimul ſunt ipſo K mino­
res; maiorem habebit proportionem triangulum ABC di­
ctas portiones, quàm ad K; inſcripta verò figura AGBNC ma
ior eſt triangulo ABC, K verò maius eſt reliquis portionibus.
Maniſeſtum est igitur figuram rectilineam ACBNC in portione in-
ſcriptam maiorem habere proportionem adreliquas portiones AOG GPB
BQN, NRC, quàm triangulum ABC ad K. ſed vt triangulum
ABC ad K, ita est CF ad FD; figura igitur inſcripta ad reliquas por­
tiones maiorem habebit proportionem, quam CF ad FD; hoc eſt LE ad
EH. Cùm ſint LH CD à lineis æquidiſtantibus LC
HD druiſæ. quare cùm figura inſcripta ad reliquas portio­
nes maiotem habeat proportionem, quàm LE ad EH; linea,
quæ ad EH eandem habeat proportionem, quàm figura inſcri­
pta ad reliquas portiones, maior erit, quam LE. Habeat igitur ME
ad EH proportionem eam, quam figura inſcripta ad portiones. Quoniam igi­
tur punctum E centrum eſt grauitatis totius portionis, figuræ autem in ipſa
inſcriptæ centrum grauitatis est punctum H: constat reliquæ magni­
tudinis ex circumrelictis portionibus compoſitæ centrum grauitatis eſſe in
linea HE producta; ita vt aſſumpta aliqua recta linea ME eam proportio
nem habeat ad EH, quam figura inſcripta ad circumrelictas portiones.
Quare magnitudinis ex circumrelictis portionibus compoſitæ centrum gra
uitatis eſt punctum M. quod est abſurdum. Ducta enim linea ST per
punctum M ipſi BD æquidiſtante, in ea omnes circumrelictæ portiones
centra grauitatis habebunt. hoc eſt magnitudinis ex portioni­
bus BPG-BQN compoſitæ centrum grauitatis eſſet in parte
MS. centrum verò grauitatis portionum AOG CRN eſſet in
parte MX; ita ut M omnium dictarum portionum eſſet gra­
uitatis centrum. quæ ſuntquidem inconuenientia. quippè
quæ etiam eodem modo ſe〈que〉ntur, ſi ST ipſi BD æquidiſtans
non eſſet. Patet igitur centrum grauitatis portionis ABC eſſe in
linea BD. quod demonſtrare oportebat.
1
2. huius.
8. quinti.
lemma.
1: tem-im 13.
primi hui
8. primi
huius.
SCHOLIVM.
In hac demonſtratione obſeruandum eſt; quòd quando Ar­
chimedes inquit, in portione autem planè inſcribatur figura &c. in­
telligendum eſt, inſcribatur primò pentagonum AGBNC
in portione planè inſcriptum; quod quidem relin〈que〉t por­
tiones AOG GPB BQN NRC, quæ ſimul uel erunt minores
ſpacio K, vel minùs. ſi non, rurſus planè adhuc inſcribatur
in portione ABC nonagonum; deinde alia figura; idquè ſem­
per fiat, donec circumrelictæ portiones ſimul ſint ſpacio K
minores. quod quidem fieri poſſe ex prima decimi Euclidis
patet. Aufertur enim ſemper maius, quam dimidium. Cùm quæ
libet portio paraboles trianguli plane in ipſa inſeripti ſit ſeſ­
quitertia. Vnde triangulum ABC maius eſt, quàm dimidium
portionis ABC. triangulum què AGB maius, quàm dimidium
portionis AGB. ſimiliter triangulum BNC portionis BNC &
ita in alijs. Quæ quidem omnia ſuntquo〈que〉 manifeſta ex vi
geſima propoſitione, eiuſquè demonſtratione de quadratura
paraboles Archimedis.
17. Archi.
de quad.
parab.
Demonſtrato centro grauitatis cuiuſlibet paraboles in eius
diametro exiſtere; oſtendet Archimedes, (vt diximus) in pa­
rabolis grauitatum centra in eadem proportione diametros
diſpeſcere. antequam autem hoc demonſtret, duas pręmittit
ſe〈que〉ntes propoſitiones ad demonſtrationem neceſſarias.
PROPOSITIO. V.
Si in portione recta linea, rectanguliquè coni
ſectione contenta rectilinea figura planè inſcriba
tur, totius portionis centrum grauitatis propinquius
eſt vertici portionis, quam centrum figuræ inſcriptæ.
1
Sit portio ABC, qualis dictaest, ipſius verò diameter ſit BD.
primùmquè in ipſa planè inſeribatur triangulum ABC. & diuidatur
BD in E, ita vt dupla ſit BE ipſius ED. erit vtiquè trtanguli ABC
centrum grauitatis punctum E. Diuidatur ità〈que〉 biſariam vtra〈que〉
AB BC in punctis FG. & punctis FG ipſi BD ducantur æquidi­
ſtantes FK GL. erit ſanè portionis AkB centrum grauitatis in linea
Fk. portionis verò BLC centrum grauit atis erit in linea GL. ſint ita­
〈que〉 puncta HI. connectanturquè HI FG. quæ BD ſecent in QN.

erit vti〈que〉 punctum Q vertici B propinquius, quàm N.
verò eſt BF ad FA, vt BG ad GC, erit FG æquidiſtansipſi AC,
eritquè FN ad NG, vt AD ad DC. eſt verò AD ipſi DC æqua­
lis, ergo FN NG inter ſe ſunt æquales. quoniam autem FN
eſt ipſi AD æquidiſtans, erit AF ad FB, vt DN ad NB. eſt
tem AF dimidia ipſius AB; cùm ſint AF FB ęquales ergo &
DN dimidia eſt ipſius DB. at verò quoniam DE terria eſt
pars ipſius DB, ſiquidem eſt BE ipſius ED dupla, erit pun­
ctum N propinquius vertici B portionis, quàm pun­
ctum E. Et quoniam parallelogrammum est HFGI. & æqualis est
FN ipſi NG, erit QH ipſi QI æqualis. ac propterea magnitudinis ex
vtriſ〈que〉 AkB BLC portionibus compoſitæ centrum grauitatis eſt in
medio lineæ HI, cùm portiones AKB BLC ſint æquales. erit ſcilicet
punctum 〈que〉 Quoniam autem trianguli ABC centrum grauitatis eſt
punctum E, magnitudinis verò ex vtriſquè AkB BLC compoſisæ
1eſt punctum 〈que〉 conſtat totius portionis ABC centrum grauitatis eſſe
in linea QE. hoc est inter puncta QE. Quare totius portionis centrum
grauitatis propinquius eſt vertici portionis, quam centrum grauitatis
trianguli planè inſcripti.
ante pri­
mi huius.
4. huius.
2. ſexti­
lemma ta
aliter 13.
primi hui^{9}
2. ſexti.
4. primi
buius.
ex its quæ
ante 2. hu
ius demon
ſtrata ſunt.
ex 8. pri­
mi huius.
*
102[Figure 102] 103[Figure 103]
Rurſus in portione pent agonum rectilineum AKBLC planè inſcri­
batur. ſitquè totius portionis diameter BD, vtriuſ〈que〉 autem portionis
AKB. BLC diameter ſit vtra〈que〉 KF LG. & quoniam in portione
AKB planè inſcripta est figura rectilinea trilatera AKB, totius por
tionis AKB centrum grauitatis est propinquius vertici K, quam
centrum rectilineæ figuræ AKB. ſit ita〈que〉 portionis AkB centrum
grauitatis punctum H; trianguli verò punctum 1. Rurſus autem ſit por
tionis BLC centrum grauitatis punctum M. trianguli verò BLC pun
ctum N. iunganturquè HM JN; quæ BD ſecent in punctis
QT. erit vti〈que〉 punctum Q vertici B propinquius, quam
T. & quoniam (ſi ducta eſſet FG) lineæ HM IN FG ab æ
 quidiſtantibus lineis KF BD LG in eadem diuiduntur pro­
portione. FG verò, vt oſtenſum eſt, bifariam à linea BD di­
uideretur; ergo & lineæ HM IN bifariam diuiſę proucnient.
æqualis est igitur HQ ipſi QM; & IT ipſi TN. ſed triangulo
AKB æquale est triangulum BLC; portio vero AkB portioni
BLC eſt æqualis. Demonstratum eſt enim alis in loçis portiones
1ſeſquitertias eſſe triangulorum, erit igitur magnitudinis ex vtriſ〈que〉 por-
tionibus AkB BLC compoſitæ centrum grauitatis punctum 〈que〉 magni­
tudinis verò ex vtriſ〈que〉 triangulis AKB BLC compoſitæ punctum
T. Rurſus ita〈que〉 quoniam trianguli ABC centrum grauitatis eſt punctum
E, magnitudinis verò ex vtriſ〈que〉 AkB BLC portionibus punctum
〈que〉 manifestum eſt totius portionis ABC centrum grauitatis eſſe in linea
QE ita diuiſa in O puncto, vt quam proportionem habet trian­
gulum ABC ad vtraſ〈que〉 portiones AkB BLC, eandem habeat por
tio ipſius terminum habens punctum Q, hoc eſt OQ ad portionem
minorem OE. pentagoni autem AKBLC, hoc eſt magnitudinis
ex triangulo ABC, trianguliſquè AKB BLC compoſitæ
centrum grauitatis eſt in linea ET ſic diuiſa in S, vt quam habet
proportionem triangulum ABC ad triangula AKB BLC, eande ha­
beat portio ipſius ad T terminata, hoc eſt ST ad reliquam SE.
Quoniam igitur maiorem habet proportionem triangulum ABC ad triam
gula KAB LBC, quam ad portiones AKB BLC; minora enim
ſunt triangula portionibus. habebit TS ad SE miorem pro­
portio nem, quam QO ad OE ac propterea erit punctum S
propinquiusipſi E, quàm O. Nam ſi punctum S primùm
eſſet in eodem puncto O, tunc TO ad OE, non quidem
maiorem, ſed minorem haberet proportionem, quàm
ad OE, cùm ſit TO minor QO. ſimiliter ob eadem cau
ſam ſi punctum S eſſet inter OT, minorem pro­
portionem TS ad SE, quàm QS ad SE, quare & ad huc
maiorem haberet proportionem QO ad OE, quàm TS
ad SE. neceſſe eſt igitur punctum S eſſe inter puncta OE.
Itaquè cùm punctum O ſit centrum grauitatis portionis ABC,
punctum verò S centrum ſit grauitatis rectilineæ figuræ
AK BLC; constat portionis ABC centrum grauitatis propinquius
eſſe vertici B, quàm centrum rectilineæ figuræ inſcriptæ. Et in om­
nibus rectilineis figuris in portionibus planè inſcriptis eadem eſt ratio.
quod demonſtrare oportebat.
1
prima lem
ma in 13.
primi bui^{9}.
4. primi
huius.
ex 8. pri­
mi huius.
8. quinti.
8. quinti.
8.quinti.
SCHOLIVM.
In fine primæ demonſtrationis in vltima concluſione quan­
do inquit Archimedes. Quare totius portionis centrum propinquius
eſt vertici portionis, quam trianguli planè in ſcripti Gra cus codexita ſe
habet ὢς τ̓ ἒιηκα ἐγγυτε<10>ον τᾶς τοῦ τμάματος κο<10>υφᾶς τὸ κέντ<10>ον τοῦ ὂλου
τμάματος, ἤ τοῦ ἐγγ<10>αφομένου τ<10>ιγώνου γνω<10>ίμως. verbaquè ἔιη κα malè in
terpoſita ſunt, nullumquè cum alijs rectum ſenſum habent,
quare horum loco ponerem ἐσί, vt ſenſus ſit, ὤς τἔγγύτε<10>ον ἐσι τᾶς
τοῦ τμάματος, &c.
*
104[Figure 104]
Obſeruandum autem occurrit in demonſtrationibus, ab
Archimede allatis; quòd in prima demonſtratione ſupponit
Archimedes, HFGI eſſe parallelogrammum. quòd vt ſit pa­
rallelogrammum, neceſſe eſt ſupponere centra grauitatis HI
ſecare lineas KF LG in partes inuicem proportionales. quod
tamen ſupponi poſſe minimè videtur. Et ſi quis ex quinto
poſtulato obijceret, centragrauitatis in æqualibus, ſimilibuſ­
què figuris eſſe æqualiter poſita; admitti quidem poteſt;
1niam figuræ, ipforum què centra inter ſe coaptari poſſunt. vt
omnibus figuris rectilineis ęqualibus, & ſimilib^{9} accidere po­
teſt. Hoc tamé contingere poſſe in parabolis, vt AKB BLC, vi
detur in conueniés. Nam quamuis AKB BLC ſint æquales, & ſint
etiam ſimiles; non ſunt tamen ſimiles ea ſi militudine, vt ſuntre
ctilineæ figuræ; vtantea diximus. Quod etiam perſpicuum fit ex
hoc, quia non ſemper coaptari poreiſt portio AKB cum portio­
ne BLC. non. enimſemper recta linea BC erit æqualisipſi BA; ne〈que〉;
ſectionis linea BLC ſectionis lineę BKA ęqualis exiſtet. Cum non
ſemper AC, & quæ ſuntipſi AC æquidiſtates ad rectos ſint an
gulos diametro BD. ſi.n. ęquidiſtantes lineę diametro fuerint
perpendiculares, tunc AB BC inter ſe ęquales eſſent; portio〈que〉;
AKB cum portione BLC coaptari poſſet: ſecùs autem minimè.
Quare centra grauiratis HI lineas KFLG in eadem proportio
ne ſecare minimèſupponi poſſe videtur; tùm exijs, quæ dicta
ſunt; tú quia hoc oſtendet Archimedes in ſeptima propoſitio
ne. quòd ſi adhuc non eſt demonſtratú, non poteſt quo〈que〉; ſuppo
ni; præſertim cùm ſit demonſtrabile. ac propterea demonſtra­
tio nullam videturvim haberead oſtendendum, quod propoſi­
tú fuit. Huic tamen occurri poſſevidetur cum Eutocio in exphca
tione huiusloci dicendo, hoc ſupponere Archimedé, quia por
tiones AKBBLC ſuntęquales, quarú diametri KFLG ſunt ę­
quales, & ęquidiſtantes, quæ ſimiliter diuiduntur à punctis HI;
vnde erit kG ad HF, vt LI ad IG. ex quibus colligit HF ipſi IG
æqualem eſſe; ac propterea HG parallelogrammum exiltere. Quæ tnm
reſponſio non eſt Eutocio digna. cùm ex dictis non ſit omninò
demonſtratiua, vtres mathematicę requirunt; quapropter omit
tenda eſt.hac.n.rationeſupponitur centra HI lineas KFLG in
eadem proportione ſecare.quod nullo modo ſupponi poteſt.
Quare dici poterit, & fortaſle rectiùs, quòd vis demonſtratio­
nis videtur in hoc eſſe conſtituta, vt ſupponatur puncta HI v­
bicun〈que〉; eſſe poſſe in lineis KFLG; ita vt ſiue ducta HI fuerit,
ſiue etiam non fuerit ipſi FG æquidiſtans, demonſtratio tamen
ſuam ſemper habebit vim, iden〈que〉; concludet. Nam ex præcedem.
ti patet centra grauitatis portionum AKB BLC eſſe in lineis
KF LG; hoceſt inter puncta KF, & LG. ſupponanturita〈que〉; cen­
tra grauitatis portionum AKB BLC eſſe puncta HI vbicun〈que〉;
1ſita, dummodo ſint in lineis KF LG, veluti Archimedes ipſe in
demonſtratione ſupponit. Ducatur〈que〉; HI; quæ vel ipſi FG æ­
quidiſtans erit, vel minùs: ſi eſt æquidiſtans, parallelogrammum
eſt HFGI, & vera eſt demonſtratio Archimedis. ſi verò non eſt
æquidiſtans, nihilominus veriſſima eſt eadem demonſtratio. Nam
ſi HI ipſi FG non eſt ęquidiſtans, patet in primis punctum Q propin
quius eſſe vertici B portionis ABC, quam punctum N, ac per con­
ſe〈que〉ns, quam punctum E centrum grauitatis trianguli ABC.
Etquoniam lineæ HI FG à lineis diuiduntur KF BN LG ę

quidiſtantibus, erit HQ ad QI, vt FN ad NG. eſt autem FN i­
pGNG ęqualis, ergo HQ ipſi QI ęqualis quo〈que〉 erit. ita〈que〉
quoniam portiones AKBBLC ſunt æquales, erit magnitudi­
nis ex vtriſ〈que〉 AKB BLC portionibus compoſitę centrum gra­
uitatis in medio lineę HI. ergo eritpunctum 〈que〉 quo cognito
eadem demonſtratio Archimedis oſtendet centrum grauita­
tis portionis ABC eſſe inter puncta E〈que〉 Nam ex verbis ipſius,
cùm ait, Quoniam autem trianguli ABC centrum grauitatis est
punctum E magnitudinis verò ex vtriſ〈que〉 AkB BLC compoſicæ
est punctum 〈que〉 constat totius portionis ABC centrum grauitatis
eſſe in in linea QE. hoc est inter puncta QE. Quare totius portionis
centrum grauitatis propinquius eſt vertici portionis, quàm trian­
guli planè inſcripti. manifeſtum eſt igitur centrum grauitatis por
tionis ABC, ſiuè ſit HI ipſi FG æquidiſtans, ſiue non æ.
quidiſtans, propinquius eſſe vertici B portionis, quàm centrum
1grauitatis trianguli ABC Quare cuca erba demonſtratio­
nis, cùm inquit Archimedes, & quoniam parallelogrammum est
HFGJ, & æqualisest FN ipſi NG. &c. immitando ſecun­
dam Archimedis demonſtrationem huius propoſitionis, vel
delenda ſuntverba, parallelogrammum eſt HFGI, & tamquam
ab aliquo ad dita; ita vt verba ſint hoc modo vniuerſalia, &
quoniam æqualis eſt FN ipſi NG, & quæ ſequuntur. vel ſat for­
taſſe Archimedi viſum eſt. ſe oſtendiſſe hoc contingere exi­
ſtente HI ipſi FG æquidiſtante. quòd ſi etiam non fuerit HI
æquidiſtans FG, idem ſequi tanquam notum omiſit. cùm per
facilis ſit demonſtratio, vt dictum eſt. Archimedeſquè res val
dè notas ſępè prætermittereſolet.
1.lenwaim 15
primu hu­
ius.
105[Figure 105]
Hocidem etiam conſiderari poteſt in ſecunda demonſtra
tione quamuis verba hanc difficultatem non habeant. nam ea­
dem ſequltur demonſtratio, ſiuèſit HM lineæ IN ęquidiſtás,
vel non æquidiſtans, vt ex verbis Archimedis perſpicuum
etenim manifeſtum eſt centra grauitatis portionum AKB
BLC eſſeinlineis KF LG. ſimiliter centra trian­
gulorum AKB BLC in ijsdem eſſe lineis KF LG. vt in pun­
ctis IN; quæ neceſſariò diuidunt KF LG in partes propor­
tionales, vnde FI GN euadunt æquales. & quoniam por­
tionum centra HM ſunt propinquiora verticibus KL, quam
triangulorum centra IN; ideo neceſſe eſt puncta HM in lineis
KI LN exiſtere. quare ſint puncta HM vbicú〈que〉 in lineis KI
LN conſtituta; ducta〈que〉; HM, quæ ſiuè ſit ipſi IN ęquidiſtans,
ſiuenon æquidiſtans, ſem per erit punctum Qpropinquius ver
tici B, quam T. eodem què modo erit punctum Q medium li­
neæ HM centrum grauitatis magnitudinis ex portionib^{9} AKB
BLC compoſitæ. ſiquidem portiones ſunt ęquales. quę quidem
omnia ex ipſamet demonſtratione ſunt manifeſta. ſuntquè
hæc eadem obſeruanda in duabus ſe〈que〉ntibus demonſtrationib^{9}.
4. huius.
ante 15.
primi hu­
ius.
PROPOSITIO. VI.
Data portione rectalinea, rectanguliquè coni
ſectione contenta, in portione figurarectilinea pla
ne inſcribi poteſt; ita vt linea inter centrum
1tatis portionis, & figuræ rectilineæ inſcriptæ, mi­
nor ſit propoſita recta linea.
106[Figure 106]
Data ſit portio ABC, qualis dicta est. cuius centrum grauitatis ſit
punctum H. & in ipſa planè inſcribatur triangulum ABC. ſitquè pro
poſita recta linea F. & quam proportionem habet BH ad F, eandem
habeat triangulum ABC ad ſpacium k. inportione autem ABC pla
nè inſcribatur figura rectilinea AGB LC, ita vt circumrelictæ portio
nes ANG GOB BPL LQC ſimul ſumptę ſint minoresipſo k:
ipſiuſquè figuræ inſcriptæ centrum grauitatis ſit punctum E. Dico li­
neam HE minorem eſſe ipſa F. N amſi non, vel æqualis est, vel
maior. Quoniam autem maior eſt figura rectilinea AGBLC,
quàm triangulum ABC, maius verò eſt ſpacium K portio­
nibus ANG GOB BPL LQC ſimul ſumptis, ideo rectili-
nea figura AGBLC ad circumrelictas portiones maiorem habet pro­
portionem, quàm triangulum ABC ad K. hoc est HB ad F. at ue
rò BH nonhabet minorem proportionem ad F, quàm habet ad HE.
cùmnon ſit minor HE ipſa F. ſi enim ponatur HE ipſi F
1æqualis, eandem habebit proportionem BH ad HE, quam
ad F. quæ eſt proportio trianguli ABC ad. K. vnde figu­
ra rectilinea AGBLC ad circumrelictas portiones maiorem,
habebit proportionem, quàm BH ad HE. ſi verò ponatur
HE maior, quàm F, habebit BH ad F, hoc eſt triangulum
ABC ad K maiorem proportionem, quàm BH ad HE.
multo igitur maiorem habet proportionem figura rectilinea AGBLC ad
circumrelictas portiones, quàm BH ad HE. Quare ſi fiat ut rectili­
linea figura AGBLC ad circumrelictas portiones, ſic alia quædam li­
nea ad HE. erit maior, quàm BH. ſitquè HM. Cùm enim portio­
nis ABC centrum grauitatis ſit H. figuræ verò rectilineæ AGBLC
punctum E. producta EH, aſſumptaquè aliqua recta linea proportione
babente ad EH, quam rectilineum AGBLC ad circumtelictas por­
tiones; maior erit quàm HB. habeat igitur (vt dictum eſt) MH ad
HE proportionem eam, quam habet figura AGBLC ad
quas portiones, ergopunctum M centrum est grauit atis magnitudi­
nis ex circumrelictis portionibus compoſitæ. quod eſſe non poteſt. Ducta
enimrecta linea RS per M ipſi AC æquidistante, inipſa ſunt centra
grauitatis vnicuiquè portioni reſpondentia; ita ſcilicet vt centrum
magnitudinis ex portionibus ANG GOB compoſitæ ſit in
linea RS. ſed in parte MR. in parteverò MS ſit grauitatis
centrum magnitudinis ex reliquis portionibus BPL LQC
compoſitæ; ita vt punctum M magnitudinis ex omnibus
portionibus compoſitæ centrum grauitatisexiſtat. quæ tamen
eſſe non poſſunt. quod idem accideret, ſi etiam RS ipſi AC
æquidiſtans non eſſet. Patetigitur HE minorem eſſe, quam F.
cùm ne〈que〉 maior, ne〈que〉 ęqualis eſſe poſſit. quod quidem de­
monſtrare oportebat.
A
lemma in 4.
ſecundi hui^{9}
7. quinti.
8.quinti.
8.primi hu
ius.
SCHOLIVM.
In hac quo〈que〉 demonſtratione obſeruandum eſt,
poſt quartam huius adnotauimus; nimirum ſi pentagonum
AGBLC in portione planèinſcriptum relin〈que〉ret portiones
ANG GOB BPL LQC, quæ ſimul maiores, vel etiam
1quales eſſent ſpacio K. Rurſus planè adhuc inſ cribatur in
portione ABC nonagonum, deinde altera figura, idquè ſem
per fiat, donec circumrelictę portiones ſimul ſint ſpacio K
minores. quod quidem fieri poſſe ibidem oſtendimus:
A
PROPOSITIO. VII.
Duabus portionibus ſimilibus recta linea, re­
ctanguliquè coni ſectione contentis, centra gra­
uitatum diametros in eadem proportione diſpe­
ſcunt.
107[Figure 107]
Sint duæ portiones, quales dictæ ſunt ABC EFG. quarum diame­
tri BD FH. ſitquè portionis ABC centrum grauitatis punctum K.
ipſius verò EFG punctum L. Demonstrandum est, puncta kL in
eadem proportione diametros diuidere, ita vt BK ad KD ſit, vt FL
1ad LH. ſi autemnon. ſi fieri poteſt, ſit BK ad kD, vt FM ad
MH. & in portione EFG rectilineum planè inſcribatur, ita vt linea
inter centrum grauitatis portionis, & centrum grauitatis figuræ
inſcriptæ minor ſit, quàm LM. ſitquè figuræ inſcriptæ centrum graui­
tatis punctum X. eritvtiquè punctum L propinquius
F, quàm punctum X. & quoniam LX minor eſt, quàm
LM, erit quo〈que〉 punctum X vertici F propinquius, quàm
M. Jn portione autem ABC inſcribatur figura rectilinea ſimilis figu
ræ in portione EFG inſcriptæ. hoc est ſimiliter planè, (ita nempè vt
figurę latera multitudine ęqualia habeant) cuius centrum graui­
tatis ſit punctum N. & quoniam figuræ in porrionibus pla­
nèinſcriptę habentlatera multitudine æqualia, ipſarum cen­
tra grauitatis diametros BD FH in eadem proportione diſpe­
ſcent. quare erit BN ad ND, vt FX ad XH. poſitum autem
fuitita eſſe FM ad MH, vt BK ad KD. ſi ita〈que〉 punctum
X propinquius eſt ipſi F, quàm M; erit & punctum N i­
pſi B propinquius, quàm K. eſtverò punctum K centrum
grauitatis portionis ABC, punctum verò N centrum figuræ
inſcripte; ergo centrum grauitatis figurę inſcriptæ propinquius
erit vertici portionis, quam centrum ipſius portionis. quod fieri non
potest. Manifeſtum est igitur eandem habere proportionem BK ad KD.
quam FL ad LH. quod demonſtrare oportebat.
6. huius.
5. huius.
3. huius.
SCHOLIVM.
Pręſens demonſtratio ea tantùm ratione eſſicax eſſe vide­
tur, quatenus ſupponitur punctum L vertici F propinqui^{9}
eſſe, quàm M. ex hoc enim ſequitur punctum X eſſe ipſi F
propinquius, quàm M. vnde euenitabſurdum, nempè, pum
ctum N eſſevertici B propinquius, quàm K. Quòd ſi ſup
poſitum fuerit Bk ad KD ita eſſe, vt FP ad PH; fuerit
autem P inter LF; tunc centrum grauitatis figurę in EFG
1planè inſcriptæ eſſetinter puncta PH; vnde centrum ctiam
figurę in ABC ſimiliter planè inſcriptę inter KD eueniret;
eſſetquè centrum grauitatis portionis ABC vertici B propin­
quius, quam centrum figuræ planè inſcriptæ. ideoquè nullum
accideret abſurdum. Quare ſi ſuppoſitum fuerit FP ad PH
eſſe, vt BK ad KD, tunc (vt eadem demonſtratio rei propo
ſitæ inſeruire poſſet) diuidenda eſſet diameter BD in 〈que〉 i­
ta vt BQ ad QD ſit, vt FL ad LH. & quoniam maio­
 rem habet proportionem FL ad LH, quàm FP ad PH; ſiqui­
dem maior eſt FL, quàm FP, & PH maior, quàm LH. Vtverò
FL ad LH, ita eſt BQ ad QD; & vt FP ad PH. ita BK ad KD;
maiorem quo〈que〉 habebit proportionem BQ ad QD, quàm
BK ad KD. & componendo BD ad DQ maiorem, quàm ea
dem BD ad Dk. Quare maior eſt DK, quàm D〈que〉 & ob id
punctum K propinquius erit vertici B, quàm 〈que〉 Deinde
planè inſcribenda eſſet figura in portione ABC, ita vt linea
inter centrum figuræ inſcriptæ, & centrum portionis minor
eſſet, quàm K〈que〉 & reliqua quæ ſequuntur, ita tamen, vt quę
facta ſunt in EFG, fiant in ABC; & quæ in ABC, fiant in EFG.
oſtendeturquè centrum figurę inſcriptę in portione EFG pro
pinquius eſſe vertici F, quàm centrum grauitatis ipſius portio
nis EFG. quod quidem fieri non poteſt. Ex quibus perlpi­
cuum fit demonſtrationem eſſe vniuerſalem. & hanc demom
ſtrationis partem Archimedem omiſiſſe, vt notam. Etvt an­
tea admonuimus, quòd centra grauitatis diametros in eadem
proportione diuidunt, omnibus parabolis competere intelli­
gendum eſt. ſiquidem omnes ſuntſimiles. quo demonſtrato,
in ſe〈que〉nti, quo in loco, & in qua diametri parte reperitur cem
trum grauitatis paraboles demonſtrat, quòd vt res perſpicua
reddatur; hæc priùs demonſtrabimus.
lemma in 4.
huius.
28.quinti.
addi.
10.quinti.
LEMMA. I.
Si magnitudo magnitudinis fuerit quadrupla, minorverò
magnitudo alterius magnitudinis ſit tripla, maior magnitu­
do vtrarum què ſimul magnitudinum tripla erit.
1
Quadrupla ſit magnitudo A magnitudinis BC.

ſit verò BC alterius magnitudinis CD tripla. Di
co magnitudinem A vtrarumquè ſimul BC CD,
hoc eſt BD triplam eſse. Quoniam enim BC tri­
pla eſt ipſius CD, erit componendo BC cum CD,
hoc eſt BD ipſius CD quadrupla. ſed magnitudo
quo〈que〉 A quadrupla eſt ipſius BC, eandem igitur
habetproportionem A ad BC, vt BD ad CD. &
permutando A ad BD, vt BC ad CD. & qui­
dem BC tripla ipſius CD, ergo A ipſius BD tri­
pla exiſtit. quod demonſtrare oportebat.
16.quinti.
108[Figure 108]
LEMMA. II.
Si magnitudo magnitudinis fuerit ſeſquitertia, erit magni­
tudo minor ipſius exceſſus tripla.
Sit magnitudo AB magnitudinis C ſeſquiter

tia; exceſſus verò, quo AB ſuperat C, ſit BD. Dico
magnitudinem C ipſius BD triplam eſſe. quod qui
dem ex ſe patet. Nam quoniam BD eſt exceſ­
ſus, quo AB ſuperat C. magnitudo autem AB i­
pſam C ſuperat tertia ipſius C parte, cum ſit AB
ipſius C ſeſquitertia. erit igitur BD tertia pars i­
ſius C. quare magnitudo C ipſius BD tripla
exiſtit. quod oſtendere oportebat.
109[Figure 109]
LEMMA III.
Sit magnitudo AB ipſius BC ſextupla. ſit verò AD tripla
ipſius AC. Dico BD ipſius BA ſeſquialteram eſse.
1
Quoniam. enim AD multiplex eſt ipſius AG, erit AC pars ipſi^{9}
AD. ac propterea ipſam AD metictur. rurſus quoniam AB,
hoc eſt AC vnà cum CB ſextupla eſt ipſius BC, erit diuidendo
AC ipſius CB quintupla. vndè CB ipſam AC, ac propterea etiam
ipſam AB metietur. Vta utem AC ad AD, ita fiat

CB ad aliam magnitudinem G; eritvti 〈que〉; CB ipſius
G pars tertia, cùm ſit AC ipſius AD pars quo〈que〉
tertia. Ita〈que〉 quoniam CB ad G eſt, vt AC ad AD,
erit perm utando CB ad CA, vt G ad AD. BC verò
ipſam CA metitur, eiuſquè eſt pars quinta; ergo
Gipſam quo〈que〉 AD metietur, eritquè ipſius pars
quinta. Quoniam autem BC ipſam BA metitur,
eademquè BC ipſam quo〈que〉 G metitur, erit BC
ipſarum AB G communis menſura. quia verò AB
ſextupla eſt ipſius CB, G verò eſt eiuſdem CB tri­
pla, erit AB ad G, ut ſextupla ad triplam. hoc eſt
ſe habebunt in dupla proportione. quapropter
AB dupla eſt ipſius G; ac per conſe〈que〉ns Gipſam
AB metitur. Quoniam igitur G totam AD metitur, &
ablatam AB quo〈que〉 metitur; metietur G reliquam BD. G
igitur ipſarum AB BD communis exiſtit menſura. & quoniam
AB dupla eſt ipſius G, tota verò AD eiuſdem G quintupla
exiſtit, erit reliqua BD tripla ipſius G. Ex quibusſequitur
DB ad BA ita ſe habere, vt tripla ad duplam. Quare DB
ipſius BA ſeſquialtera exiſtit. quod oſtendere oportebat.
16,quinti.
110[Figure 110]
PROPOSITIO. VIII.
Omnis portionis recta linea, rectanguliquè co
ni ſectione contentæ centrum grauitatis diame­
trum portionis ita diuidit, vt pars ipſius ad verti­
cem portionis reliquæ ad baſim ſit ſeſquialtera.
1
Sit portio ABC, qualis dicta est. ipſius verò diameter ſit BD. cen­
trum autem grauitatis ſit punctum H. oſtendendum eſt BH ipſius HD
ſeſquialteram eſſe. Planè inſcribatur in portione ABC triangulum ABC.
cuius centrum grauitatis ſit punctum E. biſariamquè diuidatur vtra­
què AB BC in punctis FG. & ipſi BD æquidiſtantes ducantur Fk
GL. erunt vti〈que〉 FK GL diametri portionum AkB BLC. ſit ita­
〈que〉 portionis AkB centrum grauitatis M; portionis verò BLC pun­
ctum N. connectantur〈que〉 FG MN kL, quæ diametrum BD ſe­

cent in punctis OQS. Quoniam igitur puncta MN in eadem
proportione diuidunt KF LG, erit KM ad MF, vt LN
NG. & componendo KF ad FM, vt LG ad GN. & per­
mutando KF ad LG, vt FM ad GN. ſuntquè KF LG
æquales; erit FM ipſi GN ęqualis; & reliqua Mk
LN æqualis. & quoniam FM GN, & Mk NL ęqui­
diſtantes, erunt FG MN KL inter ſe ęquales, & æquidiſtan­
tes. & eſt BD æquidiſtans KF, erit igitur SQ ipſi KM æ­
qualis. quia verò KF BD LG ſunt æquidiſtantes, erit MQ
QN, vt FO ad OG. Cùm autem ſit BF ad FA, vt BG ad GC,
1 crit FG ipſi AC ęquidiſtans. & vt AD ad DC, ita FO ad
OG. ſunt autem AD DC æquales, ergo FO OG, ac per con­
ſe〈que〉ns MQ QN inter ſe ſunt æquales. ita〈que〉 quoniam por
tiones AKB BLC ſunt æquales, magnitudinis ex vtriſ〈que〉 portio­
nibus AKB BLC compoſitæ centrum grauitatis erit in medio li­
 neç MN; hoc eſt erit punctum 〈que〉 & quoniam BH ad HD est,
vt KM ad MF (centra enim grauitatum portionum in ea­

dem proportione diametros ſecare neceſſe eſt) & componendo
BD ad DH, vt KF ad FM. permutandoquè vt BD ad KF,
ita HD ad MF. at verò BD quadrupla est ipſius KF. Hoc enim
in fine demonſtratum est, vbi est ſignum hoc, H. quadrupla igitur est
& DH ipſius MF. Quare & reliqua BH reliquæ kM, hoc est i­
pſius SQ, quadrupla existit. exiſtente autem tota BH, quæ com.
poſita eſt ex BS QH, & SQ, quadrupla ipſius S〈que〉 dempta
SQ ab ipſis BS QH SQ, reliqua igitur ex vtriſ〈que〉 BS QH
conſtans tripla est ipſius S〈que〉 ſit BS tripla ipſius SX. & quoniam
tota HQ cum SB ad totam QS eſt, vt ablata BS ad ab­
 latam SX; ſunt quidem triplę; erit reliqua HQ ad reliquam
QX in eadem proportione. ergo & QH ipſius XQ eſt tripla.
Et quoniam quadrupla est BD ipſius BS. hoc enim demonſtratum
eſt. ipſa verò BS ipſius SX eſt tripla; erit BD ipſius BX tripla.
1ac propterea erit XB ipſius BD pars tertia. Verùm ED ipſius
DB parstertia existit. Cùm centrum grauitatis trianguli ABC ſit
pnctum E. quod ita diuidit BD, vt BE ipſius ED
At verò quoniam totius lineæ BD (quæ compoſita eſt ex DE
EX XB) tertia pars eſt ipſa DE. & tertia quo〈que〉 ipſa BX;
reliqua igitur XE tertia est pars ipſius BD. & quoniam totius por­
tionis centrum grauitatis est punctum H; magnitudinis verò ex v­
tr〈que〉 portionibus AkB BLC compoſitæ centrum grauitatis est pun
ctum 〈que〉 trianguli verò ABC est punctum E; erit triangulum ABC
ad circumrelictas portiones AKB BLC, vt QH ad HE, triplum
autem eſt triangulum ABC portionum. Cùm totaportio ABC ſeſqui­
tertia ſit trianguli ABC, exceſſus verò, quo portio ſupe­
rat triangulum ABC, ſint portiones AKB BLC ſimul ſum
ptæ. tripla igitur est QH ipſius HE. ostenſa verò eſt etiam QH
tripla ipſius QX. quare erit QX ipſi HE æqualis. & quo­
niam HQ eſt tripla ipſius QX, erit HQ cum QX, hoc
eſt tota BX quadrupla ipſius QX, hoc eſt ipſius HE. ſi­
militer quoniam XH quadrupla eſt ipſius HE; quintupla i­
gitur eſt XH cum HE, tota ſcilicet XE ipſius EH; hoc est
DE ipſius EH. inuicem enim ſunt æquales EX ED, vt oſten­
ſum eſt. Cùm ita〈que〉 ſit DE ipſius EH quintupla; erit DE
cum EH ſextupla ipſius EH. Quare ſextupla est tota DH
ipſius HE. & eſt BD ipſius DE tripla; ſequialtera igitur eſt BH
ipſius HD. Quare centrum grauitatis H ita diuidit diame­
trum BD, vtpars BH ad HD ſeſquialtera exiſtit. quod de
monſtrare oportebat.
7. huius.
18.16 quinti
poſt primam
huius.
33. primi
34, primi
1. lemma
in 13. pri
mi huius
lemma in ali
ter 13 pri
mi huius
poſt primam
huius
4. primi hu
ius.
7. huius.
18.quinti.
16.quinti.
A
19 quinti.
19.quinti.
B
1.lemma hui^{9}
ante 1;.pri
mi huius.
8.primi hu
ius.
2.lemma
huius.
9.quinti.
3.lemma
huius.
111[Figure 111] 112[Figure 112]
SCHOLIVM.
Ea verba in demonſtratione poſita nempè Hoc enim in fine
demonſtratum eſt, vbi est ſignum hoc, H. ita credo eſſe intell igen­
da, quòd ſcilicet Archimedes alicubi, & in fine, ſiue huius, ſi­
ue alicuius alterius demonſtrationis, demonſtrauerit linea in
1BD quadruplam eſſe ipſius KF. & vbi hoc demonſtratum
erat, ibi quo〈que〉 pro ſigno poſita fuerit littera H. quod qui­
dem oſtenſum eſt à nobis paulò ante ſecundam huius propoſi
tionem; vbi etiam appoſuim us pro ſigno hanc literam H.
A
Rurſum in demonſtratione paulò infra Archimedes dixit,
Hoc enim demonstratum eſt, ſcilicet BD ipſius BS quadruplam
eſſe. ſupponit autem hoc tanquam demonſtratum poſt pri­
mam propoſitionem huius, vbi tota BD eſt ſexdccim, & BS qua
tuor, vt eodem in loco oſtenſum fuità nobis. Vel ad ea re­
ſpexit Archimedes, quæ ab ipſo in decimanona propoſitione
de quadratura paraboles demonſtra ta fuerunt. vbi circa finem
demonſtrationis oſtendit BD quadruplam eſſe ipſius BS.
B
Inuento ita〈que〉 centro grauitatis paraboles, vult Archime­
des in ueſtigare centrum grauitatis fruſti à parabole abſciſſi.
〈que〉madmodum in primo libro poſt inuentionem centri gra
uitatis trianguli, adinuenit etiam centrum grauitatis trapezij.
quod eſt tan quam fruſtum à triangulo abſciſsum. quare duo
adhuc theoremata proponit, in quorum poſtremo, vbi ſit cem
trum grauitatis fruſti demonſtrat. in ſe〈que〉nri verò quædam
demonſtrat neceſſaria, vt huiuſmodi centrum determinare
poſſit. Quoniam autem ſe〈que〉ns theorema arduum, difficile­
què ſeſe offert; non nulla priùs quibuſdam lemmatibus oſten
demus, ne ſi in demonſtratione ea inſererentur, longa nimis
euaderet, ac tædioſa demonſtratio. quæ quidem ſumma indi
get attentione. quamquàm in hoc theoremate explicando ad
vitandam obſcuritatem copioſum ſermonem adhibendum
curauimus; ne breuitati ſtudentes obſcuriores eſſemus.
LEMMA. I.
Si qua tuor magnitudines in continua fuerint proportione,
& earum exceſſus in eadem erunt proportione magnitudinum.
1
Sint quatuor magnitudines AF BH CL D in continua
proportione; vt ſcilicet ſit AF ad BH, vt BH ad CL; & CL
ad D. exceſſus verò, quo AF ſuperat BH, ſit EF. & exceſſus, quo
BH ſuperat CL, ſit GH. exceſſus deni〈que〉, quo CL ſuperat
D, ſit KL. eruntuti〈que〉 AE BH inter ſe ęquales, itidemquè

BG CL æquales. Dico EF GH KL in eadem eſſe proportio
ne, vt ſunt magnitudines AF BH CL, & vt BH CL D. Quo­
niam enim tota AF ad totam BH eſt, vt BH ad CL; hoc
vt ablata EA ad ablatam GB. erit reliqua EF ad reliquam GH;
vt AF ad BH. Pariquè ratione oſtendetur GH ad kL ita eſ­
ſe, vt BH ad CL. ergo exceſſus EF GH KL in eadem ſunt
proportione, vt magnitudines AF BH CL. quæ cùm ſint, vt
magnitudines BH CL D, ſiquidem omnes in continua ſunt
proportione; exceſſus igitur EF GH KL in eadem quo〈que〉
ſunt proportione, vt magnitudines BH CL D. quæ quidem
demonſtrare oportebat.
1
19.quinti.
113[Figure 113]
LEMMA. II.
Si tres fuerint magnitudines, & aliæ ipſis numero æquales,
& in eadem proportione, in primis magnitudinibus prima;
& ſecunda ad tertiam erunt, vt in ſecundis magnitudinibus
prima & ſecunda ad tertiam.
114[Figure 114]
Sint tres magnitudines ABC, & aliæ tres DEF in eadem pro­
portione. Dico AB ſimul ad C ita eſſe, vt DE ſimul ad F.
Quoniam enim A ad B eſt, ut D ad E, erit componendo AB
ad B, ut DE ad E. ſed vt B ad C, ita eſt E ad F. ergo ex ęquali
AB ſimul ad C eſt, vt DE ſimul ad F. quod demonſtrare opor
tebat.
18,quinti.
22.quinti.
LEMMA. III.
Si fuerit AB ad AC, vt DE ad DF. Dico exceſſum BC ad
CA ita eſſe, vt exceſſus EF ad FD.
cor.4.quinti
Quoniam enim eſt AB ad AC, vt DE ad DF, erit
1
uertendo CA ad AB, vt FD ad DE. & per conuer
ſionem rationis AC ad CB, vt DF ad FE. &
conuertendo CB ad CA, vt FE ad FD. quod demon­
ſtrare oportebat.
co.4.quinti.
115[Figure 115]
ALITER.
Quoniam enim AB eſt ad AC, vt DE ad DF, erit conuer­
tendo AC ad AB, vt DF ad DE. diuidendoquè CB ad BA, vt
FE ad ED. eſt autem AB ad AC, vt DE ad DF, erit
ex æquali BC ad CA, vt EF ad FD. quod demonſtrare
tebat.
17.quinti.
22,quinti.
LEMMA IIII.
116[Figure 116]
Si fuerint quotcun〈que〉 magnitudines ABC, & nlię ipſis nu
mero æquales DEF, & in eadem proportione. Dico vtram〈que〉
ſimul AD ad vtram〈que〉 ſimul BE, & vtram〈que〉 ſimul BE ad v­
tram〈que〉 ſimul CF eandem habere proportionem, quam ha­
bet A ad B, & B ad C.
1
Quoniam enim eſt A ad B, ut D ad E; erit AD ſimul ad
BE ſimul, vt A ad B. ſimiliter quoniam B ad C eſt, vt E ad
F, erit BE ſimul ad CF ſimul, vt B ad C. in eadem igitur ſunt
proportione AD ſimul, & BE ſimul, & CF ſimul, vt ABC.
quod demonſtrare oportebat.
12.quinti.
LEMMA. V.
Si magnitudo magnitudinis fuerit ſeſquialtera ad tres quin
tas eiuſdem erit duplex ſeſquialtera.
117[Figure 117]
Sit AB ipſius CD ſeſquialtera. ſit uerò CE tres quintæ
ipſius CD. Dico AB ad CE ita eſſe, vt quin〈que〉 ad duo. Fiat EF
ęqualis EC, erit CF ſex quintæ ipſius CD. & quoniam AB i­
pſius CD eſt ſeſquialtera, ſuperabit AB ipſam CD dimidia
ipſius CD. erit igitur AB ſeptem quintæ cum dimidia i­
pſius CD. quare CF minor eſt AB. fiat igitur AG æqua­
lis CF. erit vti〈que〉 AG ſex quintę ipſius CD. & ob id GB
ipſius CD quinta eſt pars cum dimidia. & quoniam CE eſt
eiuſdem CD tres quintæ, erit BG dimidia ipſius CE. qua­
re GB ipſam CE bis metietur. Et quoniam EF eſt æqua­
lis ipſi EC, ipſa BG bis quo〈que〉 metietur ipſam EF. quare
1totam CF, hoc eſt ipſam AG quater metietur. at verò GB ſei­
pſam ſemel metitur ipſa igitur GB totam AB quinquies metie­
tur. Ex quibus li〈que〉t GB ipſarum ABCE communem eſſe
menſuram. Et eſt quidem AB quintupla ipſius BG; ipſa verò
CE eiuſdem BG dupla. erit AB ad CE, vt quintupla ad duplam.
hoc eſt duplex ſeſquialtera. quod demonſtrare oportebat.
PROPOSITIO. VIIII.
Si quatuor lineæ in continua fuerint proportio­
ne, & quam proportionem habet minima ad exceſ
ſum, quo maxima minimam ſuperat; eandem ha­
beat quædam aſſumpta linea ad tres quintas exceſ­
ſus, quo maxima proportionalium tertiam exce­
dit: quam verò proportionem habet linea æqualis
duplæ maximæ proportionalium, & quadruplæ ſe
cundæ, & ſextuplæ tertiæ, & triplæ quartæ ad lineam
æqualem quintuplæ maximæ, & decuplæ ſecundæ,
& decuplæ tertiæ, & quintuplæ quartæ, ean-­
dem habeat quædam aſſumpta linea ad ex ceſſum,
quo maxima proportionalium tertiam ſuperat;
vtræ〈que〉 ſimul aſſumptæ lineæ erunt duæ quin­
tæ maximæ.
1
Sint quatuor lineæ proportionales AB BC BD BE, ita vt AB
ad BC ſit, vt BC ad BD. & vt BC ad BD, ita ſit BD ad BE. &
quam proportionem habet BE ad E A, eandem habeat FG adtres quin
tas ipſius AD. quam autem proportionem habet linea æqualis duplæ i­
pſius AB, & quidruplæ ipſius BC, & ſextuplæ ipſi^{9} BD, & triplæ ipſi^{9}
BE, ad lineam æqualem quintuplæ ipſi^{9} AB, ot decuplæ ipſi^{9} CB, & decuplæ
ipſi^{9} B D, & quintuplæ ipſius BE, eandem habeat GH ad AD. Oſteden
dum est FH duasquintas eſſe ipſius AB. Quoniam enim proportiona­
les ſunt AB BC BD BE, & ipſarum exceſſus AC CD DE in

eadem erunt proportione. & quoniam magnitudines AB BC BD
in continua ſunt proportione, & earum exceſſus AC CD DE
in eadem erunt proportione. quia verò tres ſunt magnitudi­
nes proportionales AB BC BD; & alię ipſis numero çquales, &
in eadem proportione AC CD DE, erit in primis magnitu­
dinibus prima, & ſecunda ad tertiam, vt in ſecundis magni­
tudinibus prima, & ſecunda ad tertiam; hoc eſt vtra〈que〉 ſimul
AB BC ad BD eandem habebit proportionem, quam vtra〈que〉 ſimul
AC CD, hoc eſt AD ad DE; & ob eandem rationem cum
tres ſint proportionales magnitudines AC CD DE, aliçquè
eodem modo proportionales BC BD BE; crit vtra〈que〉 ſimul
1AC CD, hoc eſt AD ad DE, vt vtra〈que〉 ſimul BC BD ad EB.
& omnes adomnes, quoniam ſcilicet eſt vtra〈que〉 ſimul AB BC
ad BD, vt horum dupla; erit vtra〈que〉 ſimul AB BC ad BD, vt
dupla vtriuſ〈que〉 ſimul AB BC ad duplam ipſius BD. eſt autem
vtra〈que〉 ſimul AB BC ad BD, vt AD ad DE. erit igitur AD ad
DE, vt dupla vtriuſ〈que〉 ſimul AB BC ad duplam ipſius BD.
quia veròita etiam eſt AD ad DE, vtvtra〈que〉 ſimul CB BD ad
BE; erit dupla vtriuſ〈que〉 ſimul AB BC ad duplam ipſius BD,
vtra〈que〉 ſimul CB BD ad BE. & vtra〈que〉 antecedentia vtra­
〈que〉 conſe〈que〉ntia in eadem erunt proportione: eruntquè in
antecedenti duę AB, tres BC, & ſola BD. in conſe〈que〉nti verò
erunt duæ BD cum ſola BE. erit igitur dupla ipſius AB, & tri
pla ipſius CB cum ſola BD ad duplam ipſius BD cum ſola BE,
vt vtra〈que〉 ſimul CB BD ad BE. vtra〈que〉 verò ſimul CB BD
ad BE eſt, vt AD ad DE. eandem ergo proportionem habet AD ad
DE, quam linea æqualis duplæ ipſius AB, & triplæipſius CB, & ſoli
DB adlineam æqualem duplæ ipſius BD & ſoli BE. Quoniam au­
tem linea compoſita ex dupla ipſius AB, & quadrupla ipſius
CB, & quadrupla ipſius BD, & dupla ipſius BE, maior eſt ea,
quæ compoſita eſt ex dupla ipſius AB, & tripla ipſius CB, &
ſola BD; maiorem habebit proportionem compoſita du­
pla ipſius AB, & quadrupla ipſius CB, & quadrupla ipſius BD,
& dupla ipſius BE ad compoſitam ex dupla ipſius BD cum
ſola BE, quam compoſita ex dupla ipſius AB, & tripla ipſius
CB cum ſola BD ad eandem compoſitam ex dupla ipſius BD
cum ſola EB. compoſita verò ex dupla ipſius AB, & tripla
ipſius BC cum ſola BD ad duplam ipſius BD cum ſola BE ita
oſtenſa eſt ſe habere AD ad DE. compoſita igitur ex dupla i­
pſius AB, & quadrupla ipſius BC, & quadrupla ipſius BD, &
dupla ipſius BE ad compoſitam ex dupla ipſius BD cum ſola
BE maiorem habebit proportionem, quam AD ad DE. Quam
ita〈que〉 proportionem habet linea æqualis duplæ ipſius AB, & quadruplæ
ipſius BC, & quadruplæ ipſius BD, & duplæ ipſius BE ad lineam æqualem
duplæ ipſius DB, & ad EB, eandem habebit AD adminorem ipſa DE.
habeat igitur ad DO. & quonianita ſe habet AD ad DO, vt compo
ſita ex dupla ipſius AB, & quadrupla ipſius BC, & quadrupla
ipſius BD, & dupla ipſius BE, hoc eſt compoſita ex dupla
1〈que〉 ſimul AB BE, & quadrupla vtriuſ〈que〉 ſimul BC BD. (bis
enim aſſumitur AB, & bis BE, quater verò BC, & quater BD)
ad compoſitam ex dupla ipſius BD cum ſola BE; erit conuer­
rendo, ut OD ad DA, ita compoſita ex dupla ipſius BD cum ſo­
la BE ad compoſitam ex dupla utriuſ〈que〉 ſimul AB BE, & qua­
 drupla vtriuſ〈que〉 ſimul BCBD. et vtræ〈que〉 ad primas eandem habe
bunt proportionem. hoc eſt componendo erit OA ad AD, vt con­
poſita ex dupla ipſius BD cum ſola BE, & dupla vtriuſ〈que〉 ſi­
mul AB BE, & quadrupla vtriuſ〈que〉 ſimul BC BD ad compo­

ſitam ex dupla vtriuſ〈que〉 ſimul AB BE, & quadrupla vtrius〈que〉;
ſimul BC BD. In hoc autem antecedente bisſumitur AB, qua
ter BC, ſexies verò BD, & ter BE. habebit igitur OA ad AD ean­
demproportionem, quam linea æqualis duplæipſius AB, et quadruplæi­
pſius CB, et ſextuplæ ipſius BD, ettriplæ ipſius BE ad lineam compoſi­
tam ex dupla vtriuſ〈que〉 ſimul AB EB, et quadrupla vtriuſ〈que〉 ſimul
CB BD. babet autem (vt ſuppoſitum eſt) GH ad AD eandem
proportionem, quam linea æqualis duplæ ipſius AB, & qua­
druplæ ipſius BC, & ſextuplæ ipſius BD, & triplæ ipſius BE
ad lineam æqualem quintuplæ ipſius AB, & decuplæ ipſius
CB, & decuplæ ipſius BD, & quintuplæ ipſius BE, hoc eſt ad
1quintuplam vtriuſ〈que〉ſimul AB BE cum decupla vtriuſquè ſimul
CB BD. In conſe〈que〉nti.n.quinquies aſsumpta eſt AB, & quinquies
BE, decies CB, & decies BD. & conuettendo habebit AD ad
GH eandem proportionem, quam quintupla vtriuſ〈que〉 ſimul AB BE
cum decupla vtriuſ〈que〉 ſimul CB BD ad lineam compoſitam ex dupla i­
pſius AB, & quadrupla ipſius CB, & ſextuplaipſius BD, & triplai­
pſius EB. Diſsimiliter autem quàm in proportionibus ordinatis, hoc est
in perturbata proportione quoniam in primis magnitudinibus ita
ſe habet antecedens OA ad conſe〈que〉ns AD, vt in ſecundis ma
gnitudinibus antecedens compoſita nempè ex dupla ipſius
AB, & quadrupla ipſius BC, & ſextupla ipſius BD, & tripla
ipſius BE, ad conſe〈que〉ns lineam ſcilic et compoſitam ex du­
pla vtriuſ〈que〉 ſimul AB BE, & quadrupla vtriuſ〈que〉 ſimul CB
BD: ut autem in primis magnitudinibus conſe〈que〉ns AD ad
aliud quippiam GH, ita in ſecundis magnitudinibus aliud
quippiam, nempèlinea compoſita ex quintupla vtriuſ〈que〉 ſi­
mul AB BE cum decupla vtriuſ〈que〉 ſimul CB BD ad antece­
dens, hoc eſt ad compoſitam ex dupla ipſius AB, & quadru­
pla ipſius CB, & ſextupla ipſius BD, & tripla ipſius BE. quare
ex æquali eandemhabet proportionem OA ad GH, quam quintupla v-
triuſ〈que〉 ſimul AB BE cum decupla vtriuſ〈que〉 ſimul CB BD ad
compoſitam ex dupla vtrius〈que〉; ſimul AB BE, et quadrupla vtrius〈que〉; ſimul
CB BD. At verò quoniam quintupla ipſius AB ad duplam
eiuſdem AB eſt, vt quin〈que〉 ad duo; ſimiliter quintupla ipſi^{9}
BE ad duplam eiuſdem BE eſt, vt quin〈que〉 ad duo, erit quin­
tupla vtriuſ〈que〉 ſimul AB BE ad duplam vtriuſ〈que〉 ſimul AB
BE, vt quin〈que〉 ad duo. pariquè ratione decupla vtriuſ〈que〉 ſi­
mul CB BD ad quadruplam vtriuſ〈que〉 ſimul CB BD eſt, vt
decem ad quatuor, hoc eſt vt quin〈que〉 ad duo. & antecedentia
ad conſe〈que〉ntia in eadem erunt proportione, hoceſt compoſi­
ta ex quintupla vtriuſ〈que〉 ſimul AB BE cum decupla vtriuſ〈que〉 ſimul
CB BD ad compoſitam ex dupla vtriuſ〈que〉 ſimul AB BE, & quadru
pla vtriuſ〈que〉 ſimul CB BD proportionem habet, quam quin〈que〉 ad duo
Quare OA ad GH proportionem habet, quam quin〈que〉 ad duo. Rurſus
factum fuit AD ad DO, vt compoſita ex dupla vtriuſ〈que〉 ſi­
mul AB BE cum quadrupla vtriuſ〈que〉 ſimul CB BD ad lineam
BE vnà cum dupla ipſius BD. conuertendo etiam quoniam
1in primis magnitudinibus antecedens OD ad conſe〈que〉ns DA
eandem habet proportionem, quam in ſecundis magnitudinibus an
tecedens EB cum dupla ipſius BD ad conſe〈que〉ns, lineam ſcilicet æ­
qualem lineæ compoſitæ ex dupla vtriuſ〈que〉 ſimul AB BE cum quadru­
pla vtriuſ〈que〉 ſimul CB BD; est autem (vt antea oſtenſum eſt) &
in primis magnitudinibus conſe〈que〉ns AD ad aliud quippiam
DE, vt in ſecundis magnitudinibus aliud quippiam, linea
ſcilicet compoſita ex dupla ipſius AB, & tripla ipſius CB, & ſola BD
ad antecedens, nempè lineam æqualem ipſi EB, & duplæ ipſius BD.

Non igitur perinde, vt in proportione ordinata; hoc est, perturbata exiſtem
te proportione, ex æqualiest OD ad DE, vt duplaipſius AB cum tripla
ipſius BC & ſola BD ad compoſitam ex dupla vtriuſ〈que〉 ſimul AB BE,
& quadrupla vtriuſ〈que〉 ſimul CB BD. ſuperat verò DE ipſam
DO exceſſu OE; linea verò compoſita ex dupla vtriuſ〈que〉 ſimul
AB BE, & quadrupla vtriuſ〈que〉 ſimul CB BD lineam excedit
compoſitam ex dupla ipſius AB cum tripla ipſius BC, ac ſola
BD, exceſſu lineæ, quæ ſit æqualis ſoli CB cum tripla ipſius
BD, & dupla ipſius BE. Quare est EO ad ED, vt CB cum tripla
ipſius BD, & dupla ipſius EB ad duplam vtriuſ〈que〉 ſimul AB BE,
& quadruplam vtriuſ〈que〉 ſimul CB BD. est autem in lineis
1portionalibus initio expoſitis; cùm in continua ſint propor­
tione, tertia in ordine BD ad quartam BE, vt prima AB ad
ſecundam BC, quare diuidendo vt DE ad EB, ita AC
CB. Rurſus quoniam in lineis proportionalibus ob eandem
cauſam CB ad BD ita eſt, vt DB ad BE; erit diuidendo, vt
CD ad DB, ita DE ad EB. ego vt DE ad EB, ita AC ad
CB, & CD ad DB. ac propterea ſecundum multiplicem compoſitio
nemtripla ipſius CD, adtriplam ipſius DB eſt, vt ſola CD ad ſo­
lam DB. & dupla ipſius DE ad duplam ipſius EB eſt,
vt DE ad EB. eſt verò CD ad DB, vt DE ad
EB, & AC ad CB; erit igitur AC ad CB, vt tripla ipſius
CD ad triplam ipſius DB; & vt dupla ipſius DE ad
duplam ipſius EB. Quare & tria antecedentia ſimul
tria ſimul conſe〈que〉ntia, hoc eſt, compoſita ex AC, &
tripla ipſius CD, & dupla ipſius DE ad compoſitam ex CB,
& tripla ipſius DB, & dupla ipſius EB ita erit, vt AC
ad CB, hoc eſt, DE ad EB. Rurſus ita〈que〉 diſsimili modo,
quàm in proportionibus ordinatis, hoc est in perturbata proportione,
quoniam eſt in primis magnitudinibus antecedens OE ad
conſe〈que〉ns ED, ita in ſecundis magnitudinibus an tecedens
compoſita ſcilicet ex CB, cum tripla ipſius BD, & dupla ip­
ſius EB, ad conſe〈que〉ns nem pè compoſitam ex dupla vtriuſ­
〈que〉 ſimul AB BE, cum quadrupla vtriuſ〈que〉 ſimul CB BD:
in primis verò magnitudinibus conſe〈que〉ns DE ad aliud quip
piam EB eſt, vt in ſecundis magnitudinibus aliud quippia,
hoc eſt compoſita ex AC cum tripla ipſius CD, & dupla ip­
ſius DE ad antecedens, lineam ſcilicet compoſitam ex CB cum
tripla ipſius BD, & dupla ipſius EB. ex æquali eandem
habebit proportionem EO ad EB, quam AC cum tri
pla ipſius CD, & dupla ipſius DE ad duplam vtriuſ
〈que〉 ſimul AB BE cum qnadrupla vtriuſ〈que〉 ſimul CB
BD. & componendo erit OB ad BE, vtlinea
cum tripla ipſius CD, & dupla ipſius DE, & dupla
vtriuſ〈que〉 ſimul AB BE, & quadrupla vtriuſ〈que〉 ſi­
mul CB BD, ad duplam vtriuſ〈que〉 ſimul AB BE
cum quadrupla vtriuſ〈que〉 ſrmul CB BD. In hoc autem
1antecedente aſſumitur ſola AC, ter CD, bis DE, bis AB,
bis BE, quater CB, & quater BD. Duæ verò AB vnà
cum ſola AC, & ſola. CB, ex quatuor vicibus, quibus ip­
ſa CB ſumitur, ſunt æquales tribus AB. tres autem CB,
quæ relictæ ſunt, vnà cum tribus CD, & tribus BD
ex quatuor vicibus, quibus ipſa BD ſumitur, ſunt æ­
quales ſex CB. ſola verò BD, quæ relicta fuit, vnà
cum duabus DE, & duabus BE, eſt æqualis tribus
BD. linea nimirum AC cum tripla ipſius CD, &
dupla ipſius DE, & dupla vtriuſ〈que〉 ſimul AB BE,
& quadrupla vtriuſ〈que〉 ſimul CB BD, æqualis erit tri­
plæ ipſius AB, cum ſextupla ipſius CB, & tripla ip­
ſius BD. Tota igitur OB ad EB eandem habet proportio­
nem, quam linea æqualis triplæ ipſius AB cum ſextupla ip­
ſius CB & tripla ipſius BD ad duplam vtriuſ〈que〉 ſimul
AB BE cum quadrupla vtriuſ〈que〉 ſimul CB BD. &
quoniam initio oſtenſum fuit lineas AC CD DE in eadem
eſſe proportione, vt ſunt quatuor lineæ continuè pro­
portionales AB BC BD BE; erunt tres AC CD
DE, & tres AB BC BD, & tres BC BD BE
in eadem proportione. conuertendo igitur in eadem quo­
〈que〉 erunt proportione. quare tres ED DC CA, &
tres BE BD BC, & tres BD BC BA in eadem ſunt proportione.
Quoniam autem BE BD BC ita ſe habent, vt BD BC BA;
vtra〈que〉 ſimul BE BD advtram〈que〉 ſimul BD BC, &
vtra〈que〉 ſimul BD BC ad vtram〈que〉 ſimul BC BA
ita ſe habebunt, vt BE BD BC. hæ verò BE BD
BC ſunt, vt ED DC CA. ergo & vtra〈que〉 ſimul
vna〈que〉〈que〉 ipſarum EB BD, DB BC, CB BA, ita ſe
habebunt, vt ED DC CA. quare erit & antecedens
ED ad ſuas conſe〈que〉ntes DC CA ſimul ſumptas,
hoc eſt ad DA, vt antecedens vtra〈que〉 ſimul EB BD
ad ſuas conſe〈que〉ntes, nempè ad vtran〈que〉 ſimul DB BC
cum vtra〈que〉 ſimul CB BA. & componendo EA ad AD,
vt vtra〈que〉 ſimul EB BD cum vtra〈que〉 ſimul AB BC,
& vtra〈que〉 ſimul CB BD ad vtram〈que〉 ſimul BD BC
1cum vtraue ſimul CB BA. In hoc autem antecedenti ſemel
ſumitur EB, & ſemel AB, bis BD, & bis BC. in conſe〈que〉ntive
rò ſumitur ola BD, ſolaquè BA, & bis BC. Proportio igitur
ipſarum EA AD eſt eadem, quæ est vtra〈que〉 ſimul EB BA cum du
pla vtriuſ〈que〉 ſimul DB BC ad vtram〈que〉 ſimul BD BA cum dupla
ipſius BC. Quare & dupla ad duplam eandem habebit proportionem hoc
est, vt EA ad AD, ita dupla vtriuſ〈que〉 ſimul EB BA cum quadru­
pla vtriuſ〈que〉 ſimul CB BD ad duplam vtriuſ〈que〉 ſimul AB BD cum

quadrupla ipſius CB. Quapropter EA adtres quintas ipſius AD eſt, vt
compoſita ex dupla vtriuſ〈que〉 ſimul AB BE, & qua-
drupla utrivs〈que〉 ſimul CB BD ad tres quintas lineæ com
poſitæ ex dupla vtriuſ〈que〉 ſimul AB BD, & quadruplaipſius CB. Ve­
rùm quia initio aſſumptum fuitita eſſe BE ad EA, vt FG ad
tres quintas ipſius AD, erit conuertendo EA ad EB,
tres quintæ ipſius AD ad FG; permutandoquè vt EA ad
tres quintasipſius AD, ſic eſt EB ad FG, vtigitur EB ad FG,
ſic dupla vtriuſ〈que〉 ſimul AB BE cum quadrupla vtriuſ〈que〉
1ſimul DB BC ad tres quintas lineæ compoſitæ ex dupla vtriuſ〈que〉 ſi­
mul AB BD cum quadrupla ipſius CB. osten ſum eſt aut OB ad EB
ita eſſe, vt tripla ipſius AB cum ſextupla ipſius CB, & tripla i­
pſius BD ad duplam vtriuſ〈que〉 ſimul AB BE cum quadrupla
vtriuſ〈que〉 ſimul CB BD. At in hoc antecedente ter aſſumpta
eſt AB, terquè BD, & ſexies CB. erit ita〈que〉 in primis magni­
tudinibus antecedens OB ad conſe〈que〉ns EB, vt in ſecundis
magnitudinibus an recedens tripla ſcilicet vtriuſ〈que〉 ſimul AB
BD cum ſextupla ipſius CB ad conſe〈que〉ns nempè duplam v­
triuſ〈que〉 ſimul AB BE, & quadruplam vtriuſ〈que〉 ſimul CB BD.

in primis verò magnitudinibus eſt conſe〈que〉ns EB ad aliud
quippiam FG, ut in ſecundis magnitudinibus conſe〈que〉ns,
hoc eſt dupla vtriuſ〈que〉 ſimul AB BE cum quadrupla vtriuſ­
〈que〉 ſimul DB BC ad aliud quippiam, nempè ad tres quintas
lineæ compoſitę ex dupla vtri^{9} 〈que〉; ſimul AB BD cum quadrupla i­
 pſi^{9} CB. Ex æquali igitur eſt, ut OB ad FG, ita linea compoſita ex tripla
utrius〈que〉 ſimul AB BD, et ſextuplaipſi^{9} CB ad tres quintas lineæ compoſi
tæ ex dupla utri^{9} 〈que〉; ſimul AB BD, & quadrupla ipſius CB. at uerò tri
pla ipſius AB ad duplam eiuſdem AB eſt, vt tria ad duo. ſimiliter
tripla ipſius BD ad duplam eiuſdem BD eſt, vt tria ad duo.
1pariquè ratione ſextupla ipſius CB ad quadruplam ciuſdem,
CB ita ſe habet, vt ſex ad quatuor, hoceſt tria ad duo, & om­
nesad omnes, hoc eſt compoſita ex tripla vtriuſ〈que〉 ſimul AB BD,
et ſextupla ipſius CB ad compoſitam ex dupla vtriuſ〈que〉 ſimul AB BD,
& quadrupla ipſius CB proportionem habet, quam tria ad duo. vt
pli gratia quindecim ad decem, ſed eadem compoſita ex tri­
pla vtriuſ〈que〉 ſimul AB BD, & ſextupla ipſius CB ad tres quin­
tas eiuſdem compofitæ ex dupla vtriuſ〈que〉 ſimul AB BD, &
drupla ipſius, CB, quæ poſita eſt decem, proportionem habet, quam
quin〈que〉 ad duo. hoc eſt ut quindecim ad ſex, tres enim quintæ
ipſius decem ſunt ſex. at verò proportio, quam habet linea com
poſita ex tripla vtriuſ〈que〉 ſimul AB BD, & ſextupla ipſius CB
ad tres quintas lineæ compoſitę ex dupla vtriuſ〈que〉 ſimul AB
BD cum quadrupla ipſius CB, eſt æqualis ei, quam habet OB
ad FG. ergo erit OB ad FG, vtquin〈que〉 ad duo. Demonstratum
autem eſt, & AO ad GH proportionem habere, quam quin〈que〉 ad duo;
totaigitur BA ad totam FH proportionem habet, quam quin〈que〉 ad duo.
ſiautem hoc, eſt quidem FH duæ quintæ ipſius AB. Quod oportebat
demonſtrare.
1.lemma hu­
ius.
2. lemma
buius.
1.lemma hu­
ius.
2. lemma
huius.
11. quinti.
12. quinti.
11, quinti.
8.quinti.
ex 8. quinti
co.4.quinti
18, quinti.
co.4.quinti.
23. quinti.
12, quinti.
co.4.quinti
23.quinti.
3.lemma hu
ius.
17. quinti.
A
12.quinti.
23.quinti.
18.quinti.
cor.4.quĩ
ti.
4.lema hu
ius.
cor.2.lem.
in 13. pri­
mi huius.
18.quinti.
B
co.4.quinti.
16,quinti.
11. quinti.
22.quinti.
C
D
5.lemma
huius.
12.quinti.
118[Figure 118] 119[Figure 119] 120[Figure 120] 121[Figure 121] 122[Figure 122]
SCHOLIVM.
Græcus codex poſt ea verba, vt DE ad EB, ita AC ad CB,
non habet, & CD ad DB, quæ ob ea, quæ ſequuntur, omninò
neceſſaria videntur. ideo poſt gręca verba, ἔσιδὲκα ὡς δε ω̄<10>ὸς εβ,
οὔτως ἄτε αγ ω̄<10>ὸς, γβ deſiderarividentur. κα ἇ γδ ω̄<10>ός δβ.
A
Vbiautem ſuntverba, vt compoſita ex dupla vtriuſ〈que〉 ſimul,
cus codex tantùm habet, οὒτως ἀ συγκειμένα ἒχτε τᾶς συυαμφοτε<10>ου.
In quibus deſideratur illa particula, dupla, ideo corrigendus eſt
hoc modo, οὔτως ὰ συγκειμένα ἒκτε τᾶς β συυαμφοτέ<10>ου, &c.
1
B
Præterea cùm inquit, ex æqualiigitur eſt vt OB ad FG, Græ­
 cus non habet, ad FG, idcirco poſt ea verba καὶ δὶσου ἄ<10>α ἐσιν ξὁς
α οβ addenda ſunt ω̄<10>ὸς ζκ.
C
Similiter quando in quit ad compoſitam ex dupla vtriuſ〈que〉 ſimul
AB BD, & quadrupla ipſius CB, græca verba ſunt ω̄<10>ο̂ς μὲν τὰν συγ­
κειμναν ἔκτε τᾶς β συναμφοτὲ<10>ου τᾶς αβ βδ τᾶς Γβ, in quib^{9} ſimiliter deli­
deratur, & quadrupla. quare ita corrigendus videtur. ω̄<10>ὸς μὲν τάν
συγκειμὲναν ἔ κ τε τας β συναμφοτέ<10>ου τᾶς αβ βδ, καὶ δ τἄς Γβ,
D
Poſtremum theorema, & ſi non habeat tantam obſcuritatem,
veluti pręcedens, non eſt tamen ſine aliqua obſcuritate, ob cu
ius intelligentiam hanc priùs propo ſitionem oſtendemus.
PROPOSITIO.
Si duæ fuerint rectæ lineę in para bolc ad diametrum ordi
natim applicatæ, erit maior parabole ad minorem, vt cubus ex
dimidia lineę maioris ad cubum ex dimidia minoris.
123[Figure 123]
In parabole ABC, cuius diameter BF, duæ ſint rectæ lineæ
ad diametrum applicatæ AC DE. Dico parabolen ABC ad
parabolen DBE eandem habere proportionem, quam cub^{9}
ex AF ad cubum ex DG. lungantur AB BC DB BE;
1què AB ipſam DG in H. Quoniam enim parabole
ſeſquitertia eſt trianguli ABC, itidemquè parabole DBE
trianguli DBE ſeſquitertia exiſtit, erit parabole ABC ad trian
gulum ABC, vt parabole DBE ad triangulum DBE. & per­
mutando parabole ABC ad parabolen DBE, vt triangulum
ABC ad triangulum DBE. Quoniam autem AC ordina­
tim eſt applicata, vnde AF ipſi FC eſt æqualis, ac per conſe­
〈que〉ns AF eſt ipſius AC dimidia. erit triangulum ABF dimi­
dium trianguli ABC. cùm vtraquè ſub eadem ſint
eademquè ratione triangulum DBG trianguli DBE dimi­
dium exiſtit. quare vt triangulum ABF ad triangulum
DBG, ita eſt triangulum ABC ad DBE triangulum, ac pro­
pterea triangulum ABF ad DBG triangulum eſt, vt parabo­
le ABC ad parabolen DBE. Cùm autem ſit HG æquidiſtans
ipſi AF, ſiquidem ſunt ordinatim applicatæ, ob triangulorum
ſimilitudinem ABF HBG, ita erit FB ad BG, vt AF ad HG
vt autem FB ad BG, ita quadratum ex AF ad quadratum
DG, erit igitur quadratum ex AF ad quadratum ex DG, vt AF
ad HG. quare lineę AF DG HG ſunt proportionales. Pro­
ducatur FB, ducaturquè à puncto D ipſi AB æquidiſtans
DK, erit vtiquè triangulorum ABF DKG anguli ABF
DHG æquales, & angulus AFB angulo DGK eſt æqualis, erit
igitur, & reliquus BAF reliquo KDG æqualis, ac propterea
triangulum ABF eſt triangulo DKG ſimile. quare triangu­
lum ABF ad triangulum DKG eam habet proportionem,
quàm AF ad DG duplicatam, hoc eſt quàm AF ad HG, quę
eſt ea, quàm habet FB ad BG. atqui triangulum ABF ad
DKG eam quo〈que〉 habet proportionem, quam FB ad GK
duplicatam. tres igitur lineę FB GK GB ſunt proportiona­
les. ex quibus ſequiturita eſſe FB ad GK, vt AF ad DG; &
GK ad GB, vt DG ad GH. ſed quoniam triangulum GDK
ad GDB (cùm ſint ſub eadem altitudine) ita eſt, vt KG
BG, ſi igitur fiat HG ad L, vt KG ad BG, erit triangulum
GDK ad triangulum GDB, vt HG ad L. Cùm autem ſit triam
gulum ABF ad DKG, vt AF ad HG, eſtquè triangulum DKG
ad DBG, vt HG ad L, erit ex ęquali triangulum ABF ad
triangulum DBG, vt AF ad L. ac propterea parabole ABC
1ad parabolen DBE eam habet proportionem, quam linea
AF ad lineam L. Quoniam autem ita eſt KG ad GB, vt
HG ad L, & vt eadem KG ad GB, ita eſt DG ad GH. vt
verò DG ad GH, ita eſt AF ad DG; crunt quatuor lineæ AF
DG HG L in continua proportione. & quoniam cubi in tri­
pla ſunt proportione laterum, erit cubus ex AF ad cubum ex
DG, vt AF ad L. cubus ergo ex AF ad cubum ex DG eam
habet proportionem, quam parabole ABC ad parabolen
DBE. quod demonſtrare oportebat.
17.34. Ar
ch.de qua.
par.
16. quinti.
ex prima
ſextt.
ex 4.ſexti.
20. primi
conicorum
Apoll. &
ex3. Arch.
de quad.
parab.
ex cor. 20.
ſexti.
1.ſexti.
11.quintl.
Oportet autem banc quoquè propoſitionem nobis eſſe cogni
tam, nem pè quòd ſolida parallelepipeda in eadem baſi conſti
tuta eam inter ſe proportionem habent, quam ipſarum alti­
tudines.
Hoc quidem à Federico Commandino in eius libro de cen
tro grauitatis ſolidorum propoſitione decimanona demon­
ſtratum fuit.
PROPOSITIO. X.
Omnis fruſti à rectanguli coni portione abſciſſi
centrum grauitatis eſt in recta linea, quæ fruſti dia­
meter exiſtit, ita poſitum, vt diuiſa linea in quin­
〈que〉 partes æquales, ſit in quinta parte media; ita
vt ipſius portio propinquior minoribaſi fruſti ad
reliquam portionem eandem habeat proportio­
nem, quam habet ſolidum baſim habens quadra­
tumex dimidia maioris baſis fruſti, altitudinem au
tem lineam æqualem vtri〈que〉 ſimul duplæ mino­
ris baſis, & maiori ad ſolidum baſim habens qua­
dratum ex dimidia minoris baſis fruſti, altitudinem
autem lineam æqualem vtri〈que〉 duplæ maioris, &
minori.
1 124[Figure 124]
Sit in rectanguli coni portione ABC duæ rectæ lineæ AC DE
æquidiſtantes. diameter verò portionis ABC ſit BF. Intelli­
gaturquè fruſtum ADEC à portione ABC abſciſſum. om­
nes vti〈que〉 lineæ ipſis AC DE æquidiſtantes in fruſto AD
EC ductæ, erunt à linea GF bifartam diuiſæ, ex quo pa­
tet quidem & ipſius ADEC diametrum eſſe GF, lineasquè AC
DE lineæ portionem in B contingenti æquidistantes eſſe. Recta
verò linea FG in quin〈que〉 partes æquales diuiſa, quinta pars me­
dia ſit HK. at〈que〉 diuidatur HK in I, ita vt HI ad
IK eandem habeat proportionem, quam habet ſolidum baſim habens
quadratum ex AF, altitudinem verò lineam æqualem vtriſ〈que〉
ſimul duplæ ipſius DG, & ipſi AF, ad ſolidum, quod
baſim habeat quadratum ex DG, altitudinem autem lineam æqua-
1
lem vtriſ〈que〉 duplæ ipſius AF, & ipſi DG. ostenden­
dum est frusti ADEC centrum grauitatis eſſe punctum 1.
ſit quidem ipſi FB æqualis MN, ipſi verò GB æqualis NO.
ſumaturquè ipſarum MN NO media proportionalis NX.
quarta verò proportionalis TN. lineæ nimirum MN NX
NO NT in continua erunt proportione. & vt TM
ad TN, ita fiat FH ad quandam lineam à puncto I, vt R, vbi­
cun〈que〉 perueniat alterum punctum R. nihil enim refert, ſiue inter
FG, ſiue inter GB cadat. & quoniam in portione rectanguli coni
ABC diameter portionis est FB; at verò BF, vel prin­
cipalis est diameter portionis, vel ducta diametro æquidistans.
lineæ verò AF DG ad ipſam ordinatim ſunt ap­
plicatæ, cùm ſint æquidistantes contingenti portionem
1in puncto B. ſi autem hoc, est vt AF ad DG potentia,
ſic FB ad BG longitudine, hoc est MN ad NO.
vt autem MN ad NO longitudine, itaest MN ad Nx potentia.
quandoquidem treslineæ MN NX NO ſunt proportio­
nales. vt igitur AF ad DG potentia, ita est MN ad N X
potentia. quare, & longitudine in eadem ſunt proportione; vt ſcili
cet AF ad DG, ita MN ad NX. ſieist ita〈que〉 cubus ex AF
ad cubum ex DG, ita cubus ex MN ad cubum ex NX. Verùm
vt cubus ex AF adcubum ex DG, ſic portio ABC ad portio­
nem DBE. vtigitur cubus ex MN ad cubum ex NX, ita
portio ABC ad portionem DBE. ſicut autem cubus ex MN
ad culum ex Nx, ita MN ad NT. cùm ſint quatuor lineæ
MN NX NO NT in continua proportione. ac propterea
eritportio ABC ad portionem DBE, vt MN ad NT.
Quare & diuidendo frustum ADEC ad portionem DBE eſt, vt
MT ad NT. Quia vero, vt factum fuit, ità eſt MT ad TN,
vt FH ad IR, eſt verò FH ipſius FG tresquintæ, erit fru­
ſtum ADEC ad portionem DBE, vt FH ad IR hoc est
tres quintæ ipſius GF ad IR. & quoniam ſolidum baſim habens qua­
dratum ex AF, altitudinem verò lineam compoſitam ex dupla ipſius
DG, & ipſa AF, ad cubum ex AF proportionem habet, quam ſo
lidi altitudo ad altitudinem cubi, ſiquidem ſunt in eadem ba
ſi. tàm emm ſolidum, quàm cubus baſim habet quadratum
ex AF. idcirco ſolidum baſim habens quadratum ex AF,
altitudinem verò lineam compoſitam ex dupla ipſius DG, &
ipſa AF ad cubum ex AF eam proportio nem habebit, quam
ſolidi altitudo, dupla, ſcilicet ipſius DG cumlinea AF ad alci­
tudinem cubi, hoc eſt ad FA. Atverò quoniam oſtenſum eſt
ita eſſe AF ad DG, vt MN ad NX, eritconuertendo DG
ad AF, vt NX ad MN, & antecedentium dupla, hoc eſt du
pla ipſius DG ad AF, vt dupla ipſius NX ad MN. & com­
ponendo dupla ipſius DG cum AF ad AF, vt dupla
NX cum MN ad MN. Quare & vt ſolidum baſim habens
quadratum ex AF, altitudinem verò lineam compoſitam ex
dupla ipſius DG cum AF ad cubum ex AF, ita dupla ipſius NX
cum linea NM ad NM. est autem cubus ex AF adcubum
ex DG, vt cubus ex MN ad cubum ex NX, vt oſtenſum eſt,
1
cubusverò ex MN ad cubum ex NX eſt, vt MN ad NT;
erit & vt cubus ex AF ad cubum ex DG, ita MN ad NT.
ſicut autem cubus ex DG ad ſolidum baſim habens quadratum ex DG,
altitudinem verò lineam compoſitam ex dupla ipſius AF, cum linea
DG, ita altitudo cubi ad altitudinem ſolidi, cum ſint in ea­
dem baſi, quadrato nempè ex DG. erit igitur vt cubus ex
DG ad ſolidum baſim habens quadratum ex DG, altitudi­
nem verò lineam compoſitam ex dupla ipſius AF cum linea
DG, ita cubi altitudo DG ad altitudinem ſolidi, ad
lineam ſcilicet compoſitam ex dupla ipſius AF, & linea
DG. Quoniam autem ita eſt AF ad DG, vt
MN ad NX, vt verò MN ad NX, ita NO
ad NT. cùm ſint MN NX NO NT in continua proportio
ne, crit AF ad DG, vt NO ad NT. & antecedentium dupla,
1hoc eſt, dupla ipſius AF ad DG, vt dupla ipſius NO ad
NT, & componendo, dupla ipſius AF cum DG
DG, vt dupla ipſius NO cum NT ad NT. & conuer­
tendo DG ad duplam ipſius AF cum DG, vt NT du­
plam ipſius NO cum NT. Quare & vt ſe habet cubus ex
DG ad ſolidum baſim habens quadratum ex DG, altitu­
dinem verò compoſitam ex dupla ipſius AF cum DG, ita
eſt TN ad compoſitam ex dupla ipſius ON, & linea TN. Ita­
〈que〉 ex ijs, quæ dicta ſunt, ita ſe habet ſolidum baſim ha­
bens quadratum ex AF, altitudinem verò lineam com­
poſitam ex dupla ipſius DG, & linea AF ad cubum
ex AF, vt dupla ipſius NX cum NM ad MN,
cubus verò ex AF ad cubum ex DG eſt, vt MN ad
NT; ita deinde ſe habetcubus ex DG ad ſolidum ba­
ſim habens quadratum ex DG, altitudinem verò lineam
compoſitam ex dupla ipſius AF, & ipſa DG, vt
NT ad compoſitam ex dupla ipſius NO, & ipſa NT.
Sunt igitur quatuor magnitudines ſolidum baſim habens quadratum
ex AF, altitudinem verò lineam compoſitam ex dupla ipſius
DG, & linea AF, & cubus ex AF, & cubus ex
DG, & ſolidum baſim habens quadratum ex DG, altitu
dinem verò lineam compoſitam: ex dupla ipſius AF, & ipſa
DG, quatuor magnitudinibus proportionales, duabus ſimul ſumptis
tineæ compoſitæ ex dupla ipſius NX & ipſa NM; & alte­
ri magnitudini MN; aliiquè deinceps NT, ac tandem lineæ
compoſitæ ex duplaipſius NO, & ipſa NT. ex æquali igitur
erit, vt ſolidum baſim habens quadratum ex AF, altitudinem
autem lineam compoſitam ex dupla ipſius DG, & ipſa AE, ad
ſolidum baſim habens quadratum ex DG, altitudinem verò lt­
neam compoſitam ex dupla ipſius AF, & ipſa DG, ita
compoſita ex dupla ipſius NX, & ipſa MN ad compoſitam
ex dupla ipſius NO, & ipſa NT ſed vt præfatum ſoii­
dum baſim habens quadratum ex AF, altitudinem verò
lineam compoſitam ex dupla ipſius DG, & ipſa AF ad
dictum ſolidum baſim habens quadratum ex DG, altitudi­
nem verò compoſitam ex dupla ipſius AF & ipſa
ita factum fuit HI ad IK. vt igitur HI ad IK, ſu
1
compoſita ex dupla ipſius NX cum MN ad compoſitam ex dupla
ipſius NO cum NT. quare & componendo HK ad KI, vt
dupla ipſius NX cum MN, & dupla ipſius NO cum NT ad
compoſitam ex dupla ipſius NO cum NT, quia verò in hoc
antecedenti ſemel ſumitur MN, & ſemel NT, bis verò NX,
& bis NO, erit HK ad KI, vt vtra〈que〉 ſimul MN NT, & du­
pla vtriuſ〈que〉 ſimul NX NO ad duplam ipſius NO, & ipſam
NT. & antecedentium quintupla. quintupla verò antecedentis
HK eſt FG, quintupla verò alterius antecedentis MN NT,
& duplæ vtriuſ〈que〉 ſimul NX NO eſt quintupla vtriuſ〈que〉 ſi­
mul MN NT, & decupla vtriuſ〈que〉 ſimul NX NO. decu­
pla enim eſt quintupla duplæ. eſt igitur FG ad IK, vt quintupla
vtriuſ〈que〉 ſimul MN NT, & decupla vtriuſ〈que〉 ſimul NX NO ad du
plam ipſius ON, & ipſam NT. & vt FG ad FK, quæeſt duæ quin
tæ ipſius FG, ita quintupla vtriuſ〈que〉 ſimul MN NT, & decupla
vtriuſ〈que〉 ſimul NX NO ad duplam vtriuſ〈que〉 ſimul MN NT,
1& quadruplam vtriuſ〈que〉 ſimul NX NO. cùm hoc quidem con
ſe〈que〉ns ſitduæ quintæ ipſius antecedentis. etenim dupla v­
triuſ〈que〉 ſimul MN NT quintuplæ earumdem ſimul MN
NT duæ quintæ exiſtit. & quadrupla vtriuſ〈que〉 ſimul NX
NO eſt duæ quintæ decuplæ earumdem NX NO. quadru­
pla enim decuplæ eſt duæ quintæ. Quoniam ita〈que〉 ita eſt FG
ad FK, vt quintupla vtriuſ〈que〉 ſimul MN NT, & decupla
vtriuſ〈que〉 ſimul NX NO ad duplam vtriuſ〈que〉 ſimul MN
NT, & quadruplam vtriuſ〈que〉 ſimul NX NO, & vt FG ad
KI, ita quintupla vtriuſ〈que〉 ſimul MN NT, & decupla vtriuſ
〈que〉 ſimul NX NO ad duplam ipſius ON, & ipſam NT:
erit FG ad ſuas conſe〈que〉ntes ſimul ſumptas FK KI,
eſt FI, vt quintupla vtriuſ〈que〉 ſimul MN NT, & decupla
vtriuſ〈que〉 ſimul NX NO ad duplam vtriuſ〈que〉 ſimul MN
NT, & quadruplam vtriuſ〈que〉 ſimul NX NO, & duplam
ipſius ON, & ipſam NT. ſed in hoc conſe〈que〉nti bis ſumi­
tur MN, quater NX, ſexies NO, & ter NT. erit igitur vt
FG æd FI, ita quintupla vtriuſ〈que〉 ſimul MN NT, & decupla v­
triuſ〈que〉 ſimul NX NO ad compoſitam ex dupla ipſius MN, & qua­
drupla ipſius NX, & ſextupla ipſius NO, & tripla ipſius NT. &
conuertendo FI ad FG, vt compoſita ex dupla ipſius
& quadrupla ipſius NX, & ſextupla ipſrus NO, & tripla ip­
ſiús NT ad quintuplam vtriuſ〈que〉 ſimul MN NT, & decu­
plam vtriuſ〈que〉 ſimul NX NO. Quoniam ita〈que〉 quatuor rectæ li
neæ MN NX NO NT ſunt continuè proportionales. factaquè
fuit MN æqualis ipſi FB, & NO ipſi GB; crit reliqua OM
ipſi FG æqualis. & vt TM ad TN ita factum fuit FH,
hoc eſt tres quintæ ipſius FG, tres ſcilicet quintæ ipſius MO
ad IR. quare & conuertendo vt NT ad TM, ita quædam aſſum­
pta linea NI ad tres quintas ipſius FG, hoc eſt ipſius MO. vt autem
compoſita ex dupla ipſius NM, & quadrupla ipſius NX, & ſextupla ip­
ſius NO & tripla ipſius NT ad lineam compoſitam ex quintupla vtrius­
〈que〉 ſimul MN NT, & decupla vtriuſ〈que〉 ſimul XN NO, ſic altera quæ
dam aſſumpta linea IF ad FG, hoc est ad MO, erit ex ſuperioribus RF
duæ quintæ ipſius MN, hoc est ipſius FB. ac propterea reliqua RB
erit tres quintæ ipſius FB. & obid BR ad. RF eſt, vt tria
duo. Quare punctum R centrum est grauitatis portionis ABC. ſit
1
quidem portionis DBE centrum grauitatis punctum Q frusti AD
EC centrum grauitatis erit in linea QR producta, quæ quiden QR
adipſain productam eandem habeat proportionem quam habet fruſium
ADEC ad reliquam portionem DBE. est autem punctum I. nam.
cùm ſit tota FB ad totam BR, vt ablata BG ad ablatam
BQ, ſunt enim vt quin〈que〉 ad tria, erit & reliqua FG ad reli­
quam QR, vt FB ad BR. ita〈que〉 quoniam tres quintæ ipſius FB
linea eſi BR; ipſius verò GB tres quintæ linea est B〈que〉 & reliquæ
igitur GF est tres quintæ QR. quoniamigitur est, vt fruſtum AD
EC adportionem DBE, ita MT ad NT, vt oſtenſum fuit; ſed vt
MN ad NT, ſic factum fuit FH ad IR, hoc eſt tres quintæ ipſius
GF; quæ est QR ad RI. erit igitur vt fruſtum ADEC adportionem
DBE, ita QR ad RI. & est quidem totius portionis ABC centrum
grauitatis punctum R; ipſius verò DBE centrum grauitatis punctum
Q: manifeſtum est igitur fruſti ADEC centrum grauitatis eſſe pun­
ctum l. quod quidem eſt in quinta parte media HK ipſius FG ab
1eo ita diuiſa, vt HI ad IK ſit, vt ſolidum baſim habens qua­
dratum ex AF, altitudinem autem duplam ipſius DG cum
AF ad ſolidum baſim habens quadratum ex DG, altitudinem
verò duplam ipſius AF cum DG. quod demonſtrare oportebat.
1 Arch de
quad. pa­
rab. &
ſecundi coni
corum A­
poll.
13.ſexti.
3.Arch.de
quad. pa­
rab. & 20.
pilmi coni
corum A­
poil.
2.cor. 20.
ſexti.
22.ſexti.
37. vndeci
mi.
17.quinti.
18.quinti.
11.quinti.
18.quinti.
cor 4.quin
ti.
22.quinti.
11.quinti.
18.quinti.
cor.2.lem­
in 13. pri­
mi huius.
cor.4.quin
ti.
ex præce­
denti.
8.buius.
8.prim hu
ius.
19.quinti.
8 prim.hu
ius.
125[Figure 125] 126[Figure 126] 127[Figure 127] 128[Figure 128]
SCHOLIVM.
In hoc Theoremate primùm obſeruanda occurrunt verba
propoſitionis, quibus Archimedes pręcipit pottionem HK
in I ita diuiſam eſſe oportere, vt HI ad IK eam habeat pro­
portionem, quam habet ſolidum baſim habens quadratum
ex dimidia maioris baſis fruſti, altitudinem autem lineam æ­
qualem vtri〈que〉 ſimul duplæ minoris baſis, & maiori ad ſoli­
dum baſim habens quadratum ex dimidia minoris baſis fru­
ſti, altitudinem autem lineam æqualem vtriſ〈que〉, duplæ ſcili­
cet baſis maioris, & minori. hoc eſt ſit HI ad IK, vt ſolidum
baſim habens quadratum ex AF, altitudinem verò lineam æ­
qualem duplæ ipſius DE cum AC ad ſolidum baſim habens
quadratum ex DG, altitudinem verò lineam æqualem vtri〈que〉
ſimul duplæ ipſius AC, & ipſi DE. In conſtructione autem
hunc propoſitionis locum explicans, & in pergreſſu totius de­
monſtrationis, inquit HI ad IK eam debere proportionem habe­
re, quam habet ſolidum baſim habens quadratum ex AF, alti
tudinem verò lineam æqualem vtri〈que〉 ſimul duplæ ipſius DG,
& ipſi AF ad ſolidum baſim habens quadratum ex DG, al­
titudinem verò lineam æqualem vtri〈que〉 ſimul duplæ ipſius
AF, & DG. Quoniam autem ſolida parallelepipeda (vt præ­
fata ſolida ſunt) in eadem baſi exiſtentia ita ſe habent interſe,
vt corum altitudine; ſolidum, quod baſim habet quadratum
ex AF, altitudinem autem duplam ipſius DE cum AC, du
plum erit ſolidi baſim habentis quadratum ex AF, altitudi­
nem verò duplam ipſius DG cum AF. Nam hæc ſolida ean
dem habent baſim, quadratum nempè ex AF; ipſorumquè
alterum habet altitudinem duplam. quia cùm ſit DE dupla
ipſius DG, erit dupla ipſius DE dupla ipſius duplæ DG;
1& AC dupla eſt ipſius AF. altitudines igitur horum ſolidorum
in dupla ſunt proportione. hoc eſt altitudo, linea ſcilicet du­
pla ipſius DE cum AC altitudinis nempè lineæ duplæ ipſius
DG cum AF dupla exiſtit. Quare ſolidum baſim habens qua­
dratum ex AF, altitudinem verò duplam ipſius DE cum AC
duplum eſt ſolidi, quod baſim habeatidem quadratum ex AF,
altitudinem verò duplam ipſius DG cum AF. cademquè ratio
neoſtendetur ſolidum baſim habens quadratum ex DG, altitu
dinem verò duplam ipſius AC cum DE duplum eſſe ſolidi ba
ſim habentis quadratum ex eadem DG, altitudinem autem du
plam ipſius AF cum DG. ſolidum igitur baſim habens qua­
dratum ex AF, altitudinem autem duplam ipſius DE cum AC
ad ſolidum quadtatum habens baſim ex AF, altitudinent verò
duplam ipſius DG cum AF eam habet proportionem, quam
habet ſolidum baſim habens quadratum ex DG, altitudinem
verò duplam ipſius AC cum AE ad ſolidum baſim habens qua
dratum ex DG, altitudinem verò duplam ipſius AF cum DG.
quare permutando primum ſolidum baſim habens quadratum
ex AF, altitudinem verò duplam ipſius DE cum AC ad ſecun­
dum ſolidum baſim habens quadratum ex DG, altitudinem
autem duplam ipſius AC cum DE eandem habet proportio­
nem, quam habet tertium ſolidum baſim habens quadratum
ex AF, altitudinem autem duplam ipſius DG cum AF ad quar
tum ſolidum baſim habens quadratum ex DG, altitudinem ve
rò duplam ipſius AF cum DG. Quapropter Archimedes loco
primi, & ſecundi ſolidi in propoſitione propoſiti rectè potuit
in demonſtratione accipere tertium, & quartum ſolidum. co
dem enim modo, & in eadem proportione linea HK in pun­
cto I diuiſa prouenit: quod quidem punctum fruſti ACED
centrum grauitatis exiſtit.
16.quinti.
Secundi libri Finis.
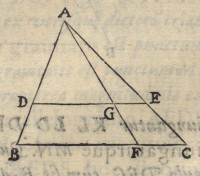
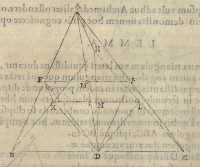
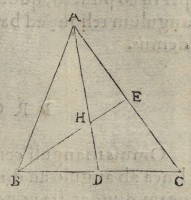
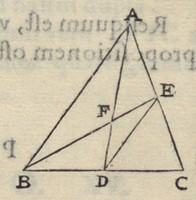
1
Erratorum quorundam reſtitutio.
Pagina 8, verſu 18, Archimedes. <33> 10, 7, ſione. <33> 18, 20, conducenti. <33> 21, 14, per
diſcere ipſum. <33> 39, 25, hoc eſt AB. <33> 43, 19, lineam. <33> 47, 20, cúm inquit, <33> 63,
20, GD DK in. <33> 65, 21, DC. Ibidem, 27, ex DC. <33> 67, 29, in maiori. <33> 69, in
poſtil: ex proxima propoſitione. <33> 70, 5, vt NL <33> 73, 1, de his, vel. <33> 84, 8, AEEB
CF FD. <33> 90, 17, totus. <33> 98, 1, quam VH. Ibidem, 7, aufertur. <33> 11, 21, repo­
ſuit. <33> 124, 19, ſectionem, <33> 140, 1, æquidiſtantes <33> 143, 11, eſt CH <33> 147, 3, cum EK ad EK, vt.
Ibide, 25, ſta S 9, ad Yα <33> 149, 19, ad χν. Ibidem, 25, eſt, vt OR. Ibidem, 27, LΓ, vt
OR ad. Ibidem, 31, vt OR ad ζδ Ibidem, 32, vt δ<10> ad <10>ζ Ibidem, 34, BD ad Bσ,
ita. Ibidem, 35, ſit BD ad Dν Ibidem, 36, BD ad Dν Bσ. <33> 150, 5, vt OR ad Oξ <33> 153,
13, ræ, vt. <33> 157, in poſtill ante 15, primi Ibidem, 17, maiorem. <33> 161, 24, erit KH.
<33> 167, 34, efficax. <33> 170, 1, ipſius AC erit. <33> 181, 36, ex dupla ipſius AB, <33> 191,
21, erunt. Ibidem, 22, DKG æquales.
REGISTRVM.
<12> ABCDEFGHIKLMNOPQRSTVXYZ,
AA BB.
Omnes duerniones, præter, BB, ternionem.
PISAVRI.
Apud Hieronymum Concordiam,
M. D. LXXXVII.