FEDERICI
COMMANDINI
VRBINATIS LIBER DE CENTRO
GRAVITATIS
SOLIDORVM.
COMMANDINI
VRBINATIS LIBER DE CENTRO
GRAVITATIS
SOLIDORVM.
 1[Figure 1]
1[Figure 1]
CVM PRIVILEGIO IN ANNOS X.
BONONIAE,
Ex Officina Alexandri Benacii.
MDLXV.
| Author: | Commandino, Federico |
| Title: | Liber de centro gravitatis solidorum |
| Date: | 1565 |
| Document ID: | MPIWG:7W21UZ74 |
| Permanent URL: | http://echo.mpiwg-berlin.mpg.de/MPIWG:7W21UZ74 |
| Copyright: | Max Planck Institute for the History of Science (unless stated otherwise) |
| License: | CC-BY-SA (unless stated otherwise) |
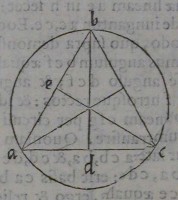 2[Figure 2]
2[Figure 2]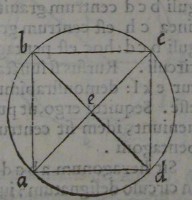 3[Figure 3]
3[Figure 3]
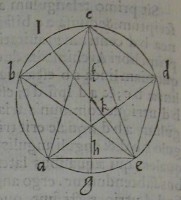 4[Figure 4]
4[Figure 4]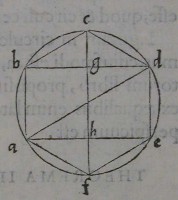 5[Figure 5]
5[Figure 5] 6[Figure 6]
6[Figure 6] 7[Figure 7]
7[Figure 7] 8[Figure 8]
8[Figure 8]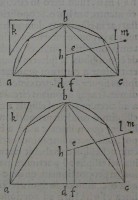 9[Figure 9]
9[Figure 9]
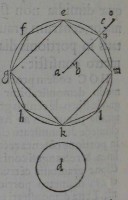 10[Figure 10]
10[Figure 10]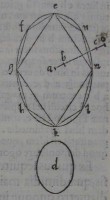 11[Figure 11]
11[Figure 11]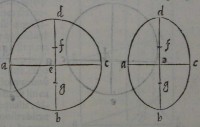 12[Figure 12]
12[Figure 12]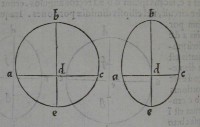 13[Figure 13]
13[Figure 13]
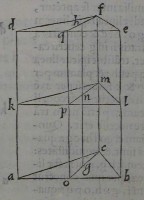 14[Figure 14]
14[Figure 14]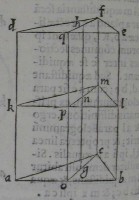 15[Figure 15]
15[Figure 15]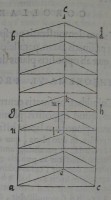 16[Figure 16]
16[Figure 16]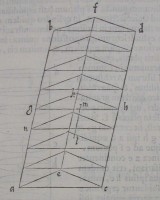 17[Figure 17]
17[Figure 17] 18[Figure 18]
18[Figure 18] 19[Figure 19]
19[Figure 19]
 20[Figure 20]
20[Figure 20] 21[Figure 21]
21[Figure 21]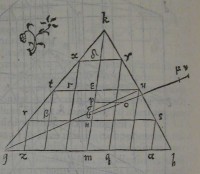 22[Figure 22]
22[Figure 22]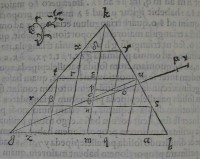 23[Figure 23]
23[Figure 23] 24[Figure 24]
24[Figure 24] 25[Figure 25]
25[Figure 25]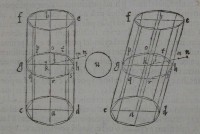 26[Figure 26]
26[Figure 26]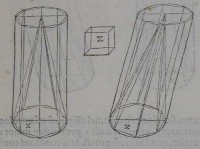 27[Figure 27]
27[Figure 27]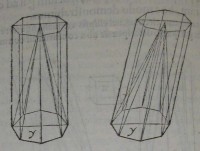 28[Figure 28]
28[Figure 28]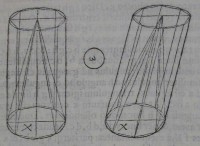 29[Figure 29]
29[Figure 29]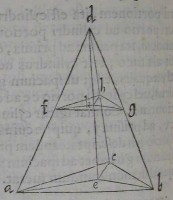 30[Figure 30]
30[Figure 30] 31[Figure 31]
31[Figure 31]
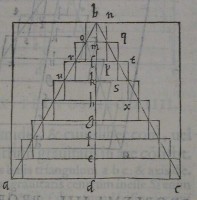 32[Figure 32]
32[Figure 32]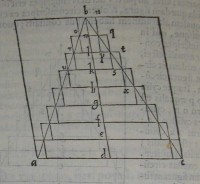 33[Figure 33]
33[Figure 33]
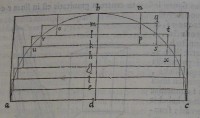 34[Figure 34]
34[Figure 34]
 35[Figure 35]quod ſit τ: iun
35[Figure 35]quod ſit τ: iun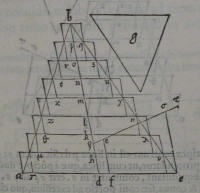 36[Figure 36]
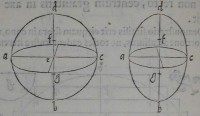
e: perque e ducatur ef axi æquidiſtans: & quam propor
36[Figure 36]
e: perque e ducatur ef axi æquidiſtans: & quam propor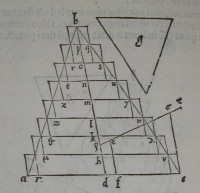 37[Figure 37]
37[Figure 37] 38[Figure 38]
38[Figure 38]
 39[Figure 39]
39[Figure 39] 40[Figure 40]
40[Figure 40]
 41[Figure 41]
41[Figure 41]
 42[Figure 42]
42[Figure 42]
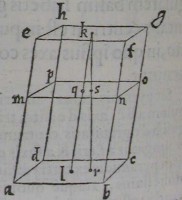 43[Figure 43]
43[Figure 43]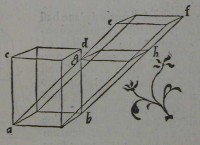 44[Figure 44]
44[Figure 44]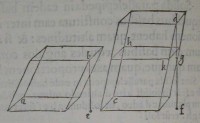 45[Figure 45]
45[Figure 45]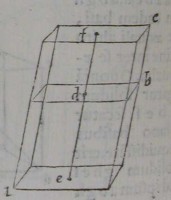 46[Figure 46]
46[Figure 46]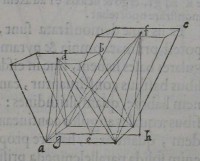 47[Figure 47]
47[Figure 47]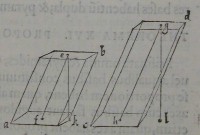 48[Figure 48]
48[Figure 48]
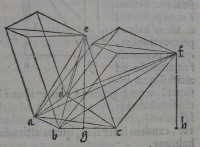 49[Figure 49]
49[Figure 49]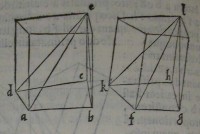 50[Figure 50]
50[Figure 50]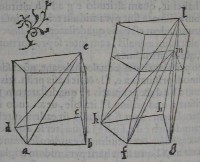 51[Figure 51]
51[Figure 51]
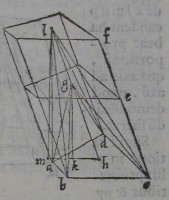 52[Figure 52]
52[Figure 52]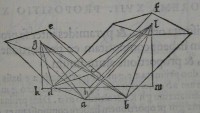 53[Figure 53]
53[Figure 53]
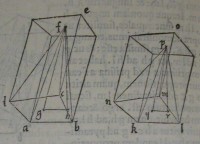 54[Figure 54]
54[Figure 54]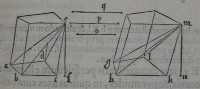 55[Figure 55]
55[Figure 55]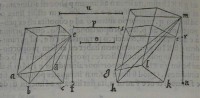 56[Figure 56]
56[Figure 56]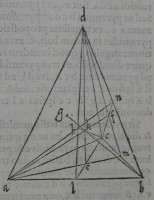 57[Figure 57]
57[Figure 57]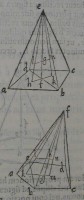 58[Figure 58]
58[Figure 58]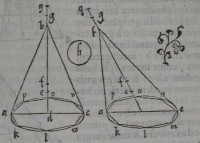 59[Figure 59]
59[Figure 59] 60[Figure 60]
60[Figure 60] 61[Figure 61]
61[Figure 61] 62[Figure 62]
62[Figure 62] 63[Figure 63]
63[Figure 63] 64[Figure 64]
64[Figure 64] 65[Figure 65]
65[Figure 65] 66[Figure 66]
66[Figure 66]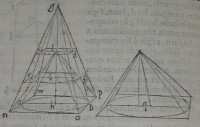 67[Figure 67]
67[Figure 67]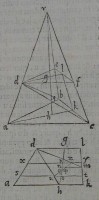 68[Figure 68]
68[Figure 68]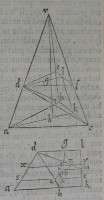 69[Figure 69]
69[Figure 69]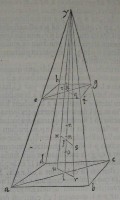 70[Figure 70]
70[Figure 70] 71[Figure 71]
71[Figure 71] 72[Figure 72]
72[Figure 72] 73[Figure 73]
73[Figure 73] 74[Figure 74]
74[Figure 74] 75[Figure 75]
75[Figure 75] 76[Figure 76]
76[Figure 76] 77[Figure 77]
77[Figure 77] 78[Figure 78]
78[Figure 78]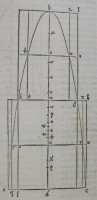 79[Figure 79]
79[Figure 79]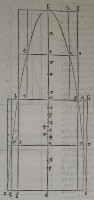 80[Figure 80]
80[Figure 80]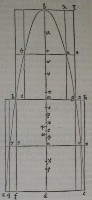 81[Figure 81]
81[Figure 81]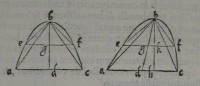 83[Figure 83]
83[Figure 83]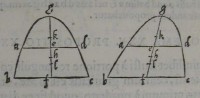 84[Figure 84]
84[Figure 84]